
Concept explainers
Figure 12-15 shows three situations in which the same horizontal rod is supported by a hinge on a wall at one end and a cord at its other end. Without written calculation, rank the situations according to the magnitudes of (a) the force on the rod from the cord, (b) the vertical force on the rod from the hinge, and (c) the horizontal force on the rod from the hinge, greatest first.
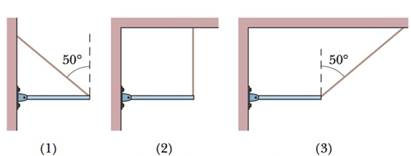
Figure 12-15 Question 1.
To rank:
a) The situations according to the magnitudes of the force on the rod from the cord.
b) The situations according to the magnitudes of the vertical force on the rod from the hinge.
c) The situations according to the magnitudes of the horizontal force on the rod form the hinge.
Answer to Problem 1Q
Solution:
a) Magnitudes of force on the rod from the cord in case (1) and (3) is same and greater than that in case (2).
b) Magnitudes of the vertical force on the rod from the hinge is same for all 3 cases.
c) Magnitudes of the horizontal force on the rod form the hinge is same in cases (1) and (3) and is zero in case (2)
Explanation of Solution
1) Concept:
We can use the concept of balancing of forces and torque at equilibrium to rank the situations according to the magnitude of the forces.
2) Formulae:
At equilibrium,
i.
ii.
3) Given:
i. The figure of rod-cable system.
ii. The angle made by the cord with the vertical direction in case 1 and 3 is 500
4) Calculation:
a) We consider the hinge point as the point of rotation. The torques acting on the rod are due to tension in the string and the weight of the rod. In all the three cases, the rod is in static equilibrium, hence:
The weight of the rod is acting at its centre and is the same in magnitude. Hence the torque equation tells us that torque due to tension, it is same in all the cases.
But the cord is making an angle with the vertical in cases (1) and (3). Hence we understand that the torque due to vertical component of the tension (T cos 50o) is the same. Since it is a component of the total tension, we know that the total tension is greater than the components in cases (1) and (3).Thus, for cases (1) and (3) the tension in the string is same and it will be greater than this in case (2).
b) We consider the hinge point as the point of rotation. In all the three cases, the rod is in static equilibrium. So the torques acting on the rod due to the tension in the string and the weight of the rod are balanced and the forces are also balanced.
Thus the vertical force from the hinge on the rod is same in all the three cases.
c) The forces acting on the rod in the horizontal direction are the force from hinge and the horizontal component of tension in the cord. In cases (1) and (3), the tension in the string is the same. Hence their corresponding horizontal components are also the same.
Thus, the horizontal force on the rod from the hinge is the same in cases (1) and (3). In case (2), there is no horizontal component of tension, hence the horizontal force from the hinge is also zero.
Conclusion:
The rod is in static equilibrium in all three cases. From the balancing conditions for torque and forces, we can determine the magnitudes of the forces acting on the rod.
Want to see more full solutions like this?
Chapter 12 Solutions
Fundamentals of Physics Extended
Additional Science Textbook Solutions
Human Physiology: An Integrated Approach (8th Edition)
Campbell Biology (11th Edition)
Organic Chemistry
Microbiology: An Introduction
Biology: Life on Earth with Physiology (11th Edition)
College Physics: A Strategic Approach (3rd Edition)
- Please help, everytime I try to input the data only one point shows on the graph. Graph of centripetal force, Fc, versus V E2 from Activity 1. Include a line of best fit and record the equation of the line.arrow_forwardBased on your graph, explain how centripetal force is affected when the hanging mass changes. Does your graph verify the relationship in the equation r = x^i + y^j = r cos ωt I + r sin ωt^j?arrow_forwardDid your experiment results in Data Table 3 verify, to within a reasonable experimental error, the condition of equilibrium of Equation 6: Στanti-clockwise = Στclockwise? Support your response with experimental data. My data shows that they are not equal to each other. So what does this mean? Thanks!arrow_forward
- Please help, everytime I try to input the data only one point shows on the graph. Graph of centripetal force, Fc, versus V E2 from Activity 1. Include a line of best fit and record the equation of the line.arrow_forwardExplain how your experiment met the condition for equilibrium in Equation 4: ΣFvertical = ΣFy = 0.arrow_forwardCan i get answer and solution for this question and can you teach me What we use to get the answer.arrow_forward
- Can i get answer and solution and can you teach me how to get it.arrow_forwardConsider a image that is located 30 cm in front of a lens. It forms an upright image 7.5 cm from the lens. Theillumination is so bright that that a faint inverted image, due to reflection off the front of the lens, is observedat 6.0 cm on the incident side of the lens. The lens is then turned around. Then it is observed that the faint,inverted image is now 10 cm on the incident side of the lens.What is the index of refraction of the lens?arrow_forward2. In class, we discussed several different flow scenarios for which we can make enough assumptions to simplify the Navier-Stokes equations enough to solve them and obtain an exact solution. Consulting the cylindrical form of the Navier-Stokes equations copied below, please answer the following questions. др a 1 a + +0x- + +O₂ = Pgr + μl 18²v, 2 ave ²v₁] az2 + at or r de r Əz dr ar Vodvz др [18 + + +Or + +Vz = Pgz +fl at ar r 20 ôz ôz dr ave дов V,Ve ave +Or + + = pge at dr r 80 Əz + az2 a.) In class, we discussed how the Navier-Stokes equations are an embodiment of Newton's 2nd law, F = ma (where bolded terms are vectors). Name the 3 forces that we are considering in our analysis of fluid flow for this class. др a 10 1 ve 2 av 2200] + +μ or 42 30 b.) If we make the assumption that flow is "fully developed" in the z direction, which term(s) would go to zero? Write the term below, describe what the term means in simple language (i.e. do not simply state "it is the derivative of a with…arrow_forward
- 1. Consult the form of the x-direction Navier-Stokes equation below that we discussed in class. (For this problem, only the x direction equation is shown for simplicity). Note that the equation provided is for a Cartesian coordinate system. In the spaces below, indicate which of the following assumptions would allow you to eliminate a term from the equation. If one of the assumptions provided would not allow you to eliminate a particular term, write "none" in the space provided. du ди at ( + + + 매일) du ди = - Pgx dy др dx ²u Fu u + fl + ax2 ay² az2 - дх - Əz 1 2 3 4 5 6 7 8 9 Assumption Flow is in the horizontal direction (e.g. patient lying on hospital bed) Flow is unidirectional in the x-direction Steady flow We consider the flow to be between two flat, infinitely wide plates There is no pressure gradient Flow is axisymmetric Term(s) in equationarrow_forwardDon't use ai to answer I will report you answerarrow_forwardwhy did the expert subtract the force exerted by the hand and the elbow by the force due to the weight of the hand and forearm and force exerted by the tricep. Does the order matter and how do you determine what to put first. Question 4 AP, CHAPTER 13 FROM BASIC BIOMECHANICS 8TH EDITIONarrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College





