
Glencoe Math Accelerated, Student Edition
1st Edition
ISBN: 9780076637980
Author: McGraw-Hill Glencoe
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Question
Chapter 11.7, Problem 11IP
To determine
To find: Vertices of each figure after a dilation.
Expert Solution & Answer
Answer to Problem 11IP
Explanation of Solution
Given information:
The dilation is
Multiply the coordinates of each vertex by
Therefore,
Coordinates after dilation are
Graph of image is
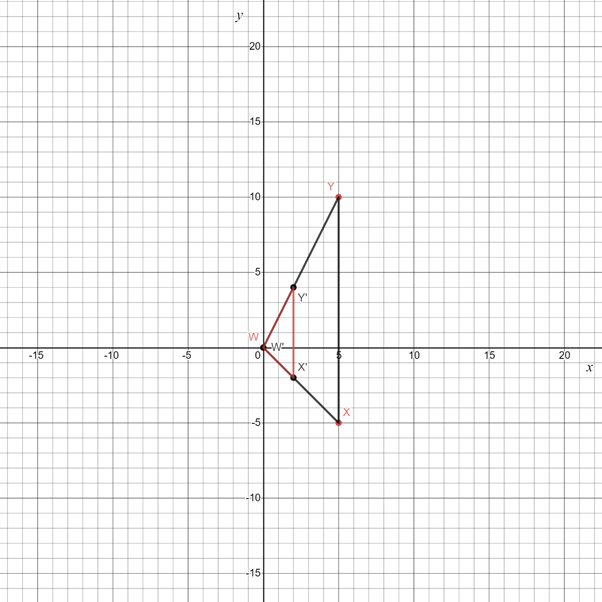
Chapter 11 Solutions
Glencoe Math Accelerated, Student Edition
Ch. 11.1 - Prob. 1GPCh. 11.1 - Prob. 2GPCh. 11.1 - Prob. 3GPCh. 11.1 - Prob. 4GPCh. 11.1 - Prob. 5GPCh. 11.1 - Prob. 6GPCh. 11.1 - Prob. 7GPCh. 11.1 - Prob. 8GPCh. 11.1 - Prob. 9GPCh. 11.1 - Prob. 10GP
Ch. 11.1 - Prob. 11IPCh. 11.1 - Prob. 12IPCh. 11.1 - Prob. 13IPCh. 11.1 - Prob. 14IPCh. 11.1 - Prob. 15IPCh. 11.1 - Prob. 16IPCh. 11.1 - Prob. 17IPCh. 11.1 - Prob. 18IPCh. 11.1 - Prob. 19IPCh. 11.1 - Prob. 20IPCh. 11.1 - Prob. 21IPCh. 11.1 - Prob. 22IPCh. 11.1 - Prob. 23IPCh. 11.1 - Prob. 24IPCh. 11.1 - Prob. 25IPCh. 11.1 - Prob. 26IPCh. 11.1 - Prob. 27IPCh. 11.1 - Prob. 28IPCh. 11.1 - Prob. 29IPCh. 11.1 - Prob. 30IPCh. 11.1 - Prob. 31IPCh. 11.1 - Prob. 32IPCh. 11.1 - Prob. 33IPCh. 11.1 - Prob. 34IPCh. 11.1 - Prob. 35HPCh. 11.1 - Prob. 36HPCh. 11.1 - Prob. 37HPCh. 11.1 - Prob. 38HPCh. 11.1 - Prob. 39STPCh. 11.1 - Prob. 40STPCh. 11.1 - Prob. 41STPCh. 11.1 - Prob. 42STPCh. 11.1 - Prob. 43CCRCh. 11.1 - Prob. 44CCRCh. 11.1 - Prob. 45CCRCh. 11.1 - Prob. 46CCRCh. 11.1 - Prob. 47CCRCh. 11.1 - Prob. 48CCRCh. 11.1 - Prob. 49CCRCh. 11.1 - Prob. 50CCRCh. 11.1 - Prob. 51CCRCh. 11.1 - Prob. 52CCRCh. 11.1 - Prob. 53CCRCh. 11.1 - Prob. 54CCRCh. 11.1 - Prob. 55CCRCh. 11.1 - Prob. 56CCRCh. 11.1 - Prob. 57CCRCh. 11.1 - Prob. 58CCRCh. 11.2 - Prob. 1GPCh. 11.2 - Prob. 2GPCh. 11.2 - Prob. 3GPCh. 11.2 - Prob. 4GPCh. 11.2 - Prob. 5GPCh. 11.2 - Prob. 6IPCh. 11.2 - Prob. 7IPCh. 11.2 - Prob. 8IPCh. 11.2 - Prob. 9IPCh. 11.2 - Prob. 10IPCh. 11.2 - Prob. 11IPCh. 11.2 - Prob. 12IPCh. 11.2 - Prob. 13IPCh. 11.2 - Prob. 14IPCh. 11.2 - Prob. 15IPCh. 11.2 - Prob. 16IPCh. 11.2 - Prob. 17IPCh. 11.2 - Prob. 18IPCh. 11.2 - Prob. 19IPCh. 11.2 - Prob. 20IPCh. 11.2 - Prob. 21IPCh. 11.2 - Prob. 22IPCh. 11.2 - Prob. 23IPCh. 11.2 - Prob. 24IPCh. 11.2 - Prob. 25IPCh. 11.2 - Prob. 26IPCh. 11.2 - Prob. 27IPCh. 11.2 - Prob. 28HPCh. 11.2 - Prob. 29HPCh. 11.2 - Prob. 30HPCh. 11.2 - Prob. 31HPCh. 11.2 - Prob. 32HPCh. 11.2 - Prob. 33STPCh. 11.2 - Prob. 34STPCh. 11.2 - Prob. 35STPCh. 11.2 - Prob. 36STPCh. 11.2 - Prob. 37CCRCh. 11.2 - Prob. 38CCRCh. 11.2 - Prob. 39CCRCh. 11.2 - Prob. 40CCRCh. 11.2 - Prob. 41CCRCh. 11.2 - Prob. 42CCRCh. 11.2 - Prob. 43CCRCh. 11.2 - Prob. 44CCRCh. 11.2 - Prob. 45CCRCh. 11.2 - Prob. 46CCRCh. 11.2 - Prob. 47CCRCh. 11.2 - Prob. 48CCRCh. 11.2 - Prob. 49CCRCh. 11.2 - Prob. 50CCRCh. 11.3 - Prob. 1GPCh. 11.3 - Prob. 2GPCh. 11.3 - Prob. 3GPCh. 11.3 - Prob. 4GPCh. 11.3 - Prob. 5GPCh. 11.3 - Prob. 6GPCh. 11.3 - Prob. 7GPCh. 11.3 - Prob. 8IPCh. 11.3 - Prob. 9IPCh. 11.3 - Prob. 10IPCh. 11.3 - Prob. 11IPCh. 11.3 - Prob. 12IPCh. 11.3 - Prob. 13IPCh. 11.3 - Prob. 14IPCh. 11.3 - Prob. 15IPCh. 11.3 - Prob. 16IPCh. 11.3 - Prob. 17IPCh. 11.3 - Prob. 18IPCh. 11.3 - Prob. 19IPCh. 11.3 - Prob. 20IPCh. 11.3 - Prob. 21IPCh. 11.3 - Prob. 22IPCh. 11.3 - Prob. 23IPCh. 11.3 - Prob. 24IPCh. 11.3 - Prob. 25IPCh. 11.3 - Prob. 26IPCh. 11.3 - Prob. 27IPCh. 11.3 - Prob. 28IPCh. 11.3 - Prob. 29IPCh. 11.3 - Prob. 30IPCh. 11.3 - Prob. 31IPCh. 11.3 - Prob. 32IPCh. 11.3 - Prob. 33IPCh. 11.3 - Prob. 34IPCh. 11.3 - Prob. 35IPCh. 11.3 - Prob. 36HPCh. 11.3 - Prob. 37HPCh. 11.3 - Prob. 38HPCh. 11.3 - Prob. 39HPCh. 11.3 - Prob. 40HPCh. 11.3 - Prob. 41STPCh. 11.3 - Prob. 42STPCh. 11.3 - Prob. 43STPCh. 11.3 - Prob. 44STPCh. 11.3 - Prob. 45CCRCh. 11.3 - Prob. 46CCRCh. 11.3 - Prob. 47CCRCh. 11.3 - Prob. 48CCRCh. 11.3 - Prob. 49CCRCh. 11.3 - Prob. 50CCRCh. 11.3 - Prob. 51CCRCh. 11.3 - Prob. 52CCRCh. 11.3 - Prob. 53CCRCh. 11.3 - Prob. 54CCRCh. 11.3 - Prob. 55CCRCh. 11.3 - Prob. 56CCRCh. 11.4 - Prob. 1GPCh. 11.4 - Prob. 2GPCh. 11.4 - Prob. 3IPCh. 11.4 - Prob. 4IPCh. 11.4 - Prob. 5IPCh. 11.4 - Prob. 6IPCh. 11.4 - Prob. 7IPCh. 11.4 - Prob. 8IPCh. 11.4 - Prob. 9IPCh. 11.4 - Prob. 10IPCh. 11.4 - Prob. 11IPCh. 11.4 - Prob. 12IPCh. 11.4 - Prob. 13IPCh. 11.4 - Prob. 14IPCh. 11.4 - Prob. 15IPCh. 11.4 - Prob. 16IPCh. 11.4 - Prob. 17IPCh. 11.4 - Prob. 18HPCh. 11.4 - Prob. 19HPCh. 11.4 - Prob. 20HPCh. 11.4 - Prob. 21HPCh. 11.4 - Prob. 22HPCh. 11.4 - Prob. 23STPCh. 11.4 - Prob. 24STPCh. 11.4 - Prob. 25STPCh. 11.4 - Prob. 26STPCh. 11.4 - Prob. 27CCRCh. 11.4 - Prob. 28CCRCh. 11.4 - Prob. 29CCRCh. 11.4 - Prob. 30CCRCh. 11.4 - Prob. 31CCRCh. 11.4 - Prob. 32CCRCh. 11.4 - Prob. 33CCRCh. 11.4 - Prob. 34CCRCh. 11.4 - Prob. 35CCRCh. 11.4 - Prob. 36CCRCh. 11.4 - Prob. 37CCRCh. 11.4 - Prob. 38CCRCh. 11.4 - Prob. 39CCRCh. 11.4 - Prob. 40CCRCh. 11.5 - Prob. 1GPCh. 11.5 - Prob. 2GPCh. 11.5 - Prob. 3GPCh. 11.5 - Prob. 4GPCh. 11.5 - Prob. 5IPCh. 11.5 - Prob. 6IPCh. 11.5 - Prob. 7IPCh. 11.5 - Prob. 8IPCh. 11.5 - Prob. 9IPCh. 11.5 - Prob. 10IPCh. 11.5 - Prob. 11IPCh. 11.5 - Prob. 12IPCh. 11.5 - Prob. 13IPCh. 11.5 - Prob. 14IPCh. 11.5 - Prob. 15IPCh. 11.5 - Prob. 16IPCh. 11.5 - Prob. 17HPCh. 11.5 - Prob. 18HPCh. 11.5 - Prob. 19HPCh. 11.5 - Prob. 20HPCh. 11.5 - Prob. 21HPCh. 11.5 - Prob. 22STPCh. 11.5 - Prob. 23STPCh. 11.5 - Prob. 24STPCh. 11.5 - Prob. 25STPCh. 11.5 - Prob. 26CCRCh. 11.5 - Prob. 27CCRCh. 11.5 - Prob. 28CCRCh. 11.5 - Prob. 29CCRCh. 11.5 - Prob. 30CCRCh. 11.5 - Prob. 31CCRCh. 11.5 - Prob. 32CCRCh. 11.5 - Prob. 33CCRCh. 11.5 - Prob. 34CCRCh. 11.5 - Prob. 35CCRCh. 11.5 - Prob. 36CCRCh. 11.5 - Prob. 37CCRCh. 11.5 - Prob. 38CCRCh. 11.5 - Prob. 39CCRCh. 11.6 - Prob. 1GPCh. 11.6 - Prob. 2GPCh. 11.6 - Prob. 3GPCh. 11.6 - Prob. 4IPCh. 11.6 - Prob. 5IPCh. 11.6 - Prob. 6IPCh. 11.6 - Prob. 7IPCh. 11.6 - Prob. 8IPCh. 11.6 - Prob. 9IPCh. 11.6 - Prob. 10IPCh. 11.6 - Prob. 11IPCh. 11.6 - Prob. 12IPCh. 11.6 - Prob. 13HPCh. 11.6 - Prob. 14HPCh. 11.6 - Prob. 15HPCh. 11.6 - Prob. 16HPCh. 11.6 - Prob. 17STPCh. 11.6 - Prob. 18STPCh. 11.6 - Prob. 19CCRCh. 11.6 - Prob. 20CCRCh. 11.6 - Prob. 21CCRCh. 11.6 - Prob. 22CCRCh. 11.6 - Prob. 23CCRCh. 11.6 - Prob. 24CCRCh. 11.6 - Prob. 25CCRCh. 11.7 - Prob. 1GPCh. 11.7 - Prob. 2GPCh. 11.7 - Prob. 3GPCh. 11.7 - Prob. 4GPCh. 11.7 - Prob. 5GPCh. 11.7 - Prob. 6IPCh. 11.7 - Prob. 7IPCh. 11.7 - Prob. 8IPCh. 11.7 - Prob. 9IPCh. 11.7 - Prob. 10IPCh. 11.7 - Prob. 11IPCh. 11.7 - Prob. 12IPCh. 11.7 - Prob. 13IPCh. 11.7 - Prob. 14IPCh. 11.7 - Prob. 15IPCh. 11.7 - Prob. 16IPCh. 11.7 - Prob. 17IPCh. 11.7 - Prob. 18IPCh. 11.7 - Prob. 19IPCh. 11.7 - Prob. 20HPCh. 11.7 - Prob. 21HPCh. 11.7 - Prob. 22HPCh. 11.7 - Prob. 23HPCh. 11.7 - Prob. 24HPCh. 11.7 - Prob. 25HPCh. 11.7 - Prob. 26STPCh. 11.7 - Prob. 27STPCh. 11.7 - Prob. 28STPCh. 11.7 - Prob. 29STPCh. 11.7 - Prob. 30CCRCh. 11.7 - Prob. 31CCRCh. 11.7 - Prob. 32CCRCh. 11.7 - Prob. 33CCRCh. 11.7 - Prob. 34CCRCh. 11.7 - Prob. 35CCRCh. 11.8 - Prob. 1GPCh. 11.8 - Prob. 2GPCh. 11.8 - Prob. 3GPCh. 11.8 - Prob. 4GPCh. 11.8 - Prob. 5IPCh. 11.8 - Prob. 6IPCh. 11.8 - Prob. 7IPCh. 11.8 - Prob. 8IPCh. 11.8 - Prob. 9IPCh. 11.8 - Prob. 10IPCh. 11.8 - Prob. 11IPCh. 11.8 - Prob. 12IPCh. 11.8 - Prob. 13IPCh. 11.8 - Prob. 14IPCh. 11.8 - Prob. 15IPCh. 11.8 - Prob. 16IPCh. 11.8 - Prob. 17HPCh. 11.8 - Prob. 18HPCh. 11.8 - Prob. 19HPCh. 11.8 - Prob. 20HPCh. 11.8 - Prob. 21STPCh. 11.8 - Prob. 22STPCh. 11.8 - Prob. 23STPCh. 11.8 - Prob. 24STPCh. 11.8 - Prob. 25CCRCh. 11.8 - Prob. 26CCRCh. 11.8 - Prob. 27CCRCh. 11.8 - Prob. 28CCRCh. 11.8 - Prob. 29CCRCh. 11.8 - Prob. 30CCRCh. 11.8 - Prob. 31CCRCh. 11.8 - Prob. 32CCRCh. 11.8 - Prob. 33CCRCh. 11.8 - Prob. 34CCRCh. 11.8 - Prob. 35CCRCh. 11 - Prob. 1CRCh. 11 - Prob. 2CRCh. 11 - Prob. 3CRCh. 11 - Prob. 4CRCh. 11 - Prob. 5CRCh. 11 - Prob. 6CRCh. 11 - Prob. 7CRCh. 11 - Prob. 8CRCh. 11 - Prob. 9CRCh. 11 - Prob. 10CRCh. 11 - Prob. 11CRCh. 11 - Prob. 12CRCh. 11 - Prob. 13CRCh. 11 - Prob. 14CRCh. 11 - Prob. 15CRCh. 11 - Prob. 16CRCh. 11 - Prob. 17CRCh. 11 - Prob. 18CRCh. 11 - Prob. 19CRCh. 11 - Prob. 20CRCh. 11 - Prob. 21CRCh. 11 - Prob. 22CRCh. 11 - Prob. 23CRCh. 11 - Prob. 24CRCh. 11 - Prob. 25CRCh. 11 - Prob. 26CRCh. 11 - Prob. 27CRCh. 11 - Prob. 28CRCh. 11 - Prob. 29CRCh. 11 - Prob. 30CRCh. 11 - Prob. 31CRCh. 11 - Prob. 32CRCh. 11 - Prob. 33CRCh. 11 - Prob. 34CR
Additional Math Textbook Solutions
Find more solutions based on key concepts
A categorical variable has three categories, with the following frequencies of occurrence: a. Compute the perce...
Basic Business Statistics, Student Value Edition
In Exercises 3–8, find the limit of each function (a) as, and (b) as . (You may wish to visualize your answer ...
University Calculus: Early Transcendentals (4th Edition)
Mathematical Connections Explain why 25 cents is one-fourth of a dollar, yet 15 minutes is one-fourth of an hou...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
A pair of fair dice is rolled. What is the probability that the second die lands on a higher value than does th...
A First Course in Probability (10th Edition)
2. Confidence Interval for Hemoglobin Large samples of women and men are obtained, and the hemoglobin level is ...
Elementary Statistics (13th Edition)
the given expression
Pre-Algebra Student Edition
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 3:59 m s ☑ D'Aniello Boutique | Fashion VOLTE danielloboutique.it/asia SUBSCRIBE NOW: 10% OFF TO USE ANYTIME YOU WANT d'aniello NEW IN WOMEN NEW IN MEN WINTER SALE: 50% OFF on FW24 SHOP WOMEN SHOP MENarrow_forwardJOB UPDATE EMERSON GRAD ENGINEER (FRESHERS) SOFTWARE ENGG NEW RELIC BROWSERSTACK (FRESHERS) SOFTWARE ENGG FULL STACK DATA ENGINEER GENPACT + PYTHON CARS24 WORK FROM HOME #vinkjobs TELE PERFORMANCE Vinkjobs.com CUSTOMER SUPPORT Search "Vinkjobs.com" on Googlearrow_forwarddo question 2 pleasearrow_forward
- question 10 pleasearrow_forward00 (a) Starting with the geometric series Σ X^, find the sum of the series n = 0 00 Σηχη - 1, |x| < 1. n = 1 (b) Find the sum of each of the following series. 00 Σnx", n = 1 |x| < 1 (ii) n = 1 sin (c) Find the sum of each of the following series. (i) 00 Σn(n-1)x^, |x| <1 n = 2 (ii) 00 n = 2 n² - n 4n (iii) M8 n = 1 շոarrow_forward(a) Use differentiation to find a power series representation for 1 f(x) = (4 + x)²* f(x) = 00 Σ n = 0 What is the radius of convergence, R? R = (b) Use part (a) to find a power series for f(x) = 1 (4 + x)³° f(x) = 00 Σ n = 0 What is the radius of convergence, R? R = (c) Use part (b) to find a power series for f(x) = x² (4 + x)³* 00 f(x) = Σ n = 2 What is the radius of convergence, R? R = Need Help? Read It Watch It SUBMIT ANSWERarrow_forward
- answer for question 4 pleasearrow_forward(3) (20 points) Let F(x, y, z) = (y, z, x²z). Define E = {(x, y, z) | x² + y² ≤ z ≤ 1, x ≤ 0}. (a) (2 points) Calculate the divergence V. F. (b) (4 points) Let D = {(x, y) | x² + y² ≤ 1, x ≤ 0} Without calculation, show that the triple integral √ (V · F) dV = √ 2²(1. = x²(1 − x² - y²) dA. Earrow_forward(2) (22 points) Let F(x, y, z) = (x sin y, cos y, ―xy). (a) (2 points) Calculate V. F. (b) (6 points) Given a vector field is everywhere defined with V G₁(x, y, z) = * G2(x, y, z) = − G3(x, y, z) = 0. 0 0 F(x, y, z) = (F₁(x, y, z), F₂(x, y, z), F(x, y, z)) that F = 0, let G = (G1, G2, G3) where F₂(x, y, y, t) dt - √ F³(x, t, 0) dt, * F1(x, y, t) dt, t) dt - √ F Calculate G for the vector field F(x, y, z) = (x sin y, cos y, -xy).arrow_forward
- Evaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √ √(x + y) A R R = {(x, y) | 25 < x² + y² ≤ 36, x < 0} Hint: The integral and Region is defined in rectangular coordinates.arrow_forwardFind the volume of the solid that lies under the paraboloid z = 81 - x² - y² and within the cylinder (x − 1)² + y² = 1. A plot of an example of a similar solid is shown below. (Answer accurate to 2 decimal places). Volume using Double Integral Paraboloid & Cylinder -3 Hint: The integral and region is defined in polar coordinates.arrow_forwardEvaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √4(1–2² 4(1 - x² - y²) dA R 3 R = {(r,0) | 0 ≤ r≤ 2,0π ≤0≤¼˜}. Hint: The integral is defined in rectangular coordinates. The Region is defined in polar coordinates.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
HOW TO FIND DETERMINANT OF 2X2 & 3X3 MATRICES?/MATRICES AND DETERMINANTS CLASS XII 12 CBSE; Author: Neha Agrawal Mathematically Inclined;https://www.youtube.com/watch?v=bnaKGsLYJvQ;License: Standard YouTube License, CC-BY
What are Determinants? Mathematics; Author: Edmerls;https://www.youtube.com/watch?v=v4_dxD4jpgM;License: Standard YouTube License, CC-BY