
Concept explainers
a)
To determine: The results of the run test.
Introduction: Run chart refers to a line graph that displays the recorded data based on the time sequence.
a)
Answer to Problem 14P
Explanation of Solution
Given information:
| Test | z-score |
| Median | +1.37 |
| Up/Down | +1.05 |
By observing the given data of median +1.37 (< ±2) and up/down +1.05 (< ±2), it can be concluded that they are within the statistical limits of ±2.
Hence, the result of the run test suggests that the output possess randomness.
b)
To determine: The results of the run test.
Introduction: Run chart refers to a line graph that displays the recorded data based on the time sequence.
b)
Answer to Problem 14P
Explanation of Solution
Given information:
Formula:
Calculation of expected number of runs:
Observed number of runs = 14
The expected number of runs is calculated by adding half of the total number of samples with 1 which gives 11.
Calculation of standard deviation:
Standard deviation is calculated by subtracting number of sample 20 from 1 and dividing the resultant by 4 and taking square for the value which yields 2.18.
The z factor for median is calculated by dividing the difference of 14 and 11 with 2.18 which yields +1.38 which is within the test statistics of ±2.00 and no non-randomness exist.
Up/Down Test:
The observed number of runs is 8.
Calculation of expected number of runs:
The expected number of runs is calculated by subtracting the double of the number of samples 20 and subtracting from1 and dividing the resultant with 3 which gives 13.
Calculation of standard deviation:
Standard deviation is calculated by multiplying the number of samples with 16 and subtracting the resultant from 29 and then dividing the resulting value with 90 and taking square root which yields 1.80.
The z factor for median is calculated by dividing the difference of 8 and 13 with 1.80 which yields -2.78 which is beyond the test statistics of ±2.00 which is non-random.
Hence, the result of the median run test is random and up/down test is no non randomness is detected.
c)
To determine: The results of the run test.
Introduction: Run chart refers to a line graph that displays the recorded data based on the time sequence.
c)
Answer to Problem 14P
Explanation of Solution
Given information:
| Cable | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Defects | 2 | 3 | 1 | 0 | 1 | 3 | 2 | 0 | 2 | 1 | 3 | 1 | 2 | 0 |
Formula:
Analysis of data:
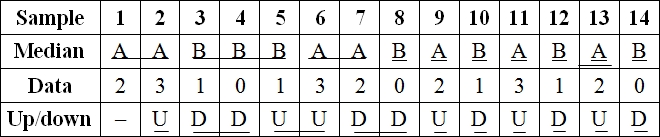
To make analysis of data, the given data is compared with median (center line) to make A/B and U/D which is shown below,
Median run test:
From analysis, the observed number of runs is 10 and median is 1.5.
Calculation of expected number of runs:
The expected number of runs is calculated by adding half of the total number of samples with 1 which gives 8.
Calculation of standard deviation:
Standard deviation is calculated by subtracting number of sample 14 from 1 and dividing the resultant by 4 and taking square for the value which yields 1.80.
The z factor for median is calculated by dividing the difference of 10 and 8 with 1.80 which yields +1.11 which is within the test statistics of ±2.00 and no non-randomness exist.
Up/Down Test:
The observed number of runs from the analysis is 10.
Calculation of expected number of runs:
The expected number of runs is calculated by subtracting the double of the number of samples 14 and subtracting from1 and dividing the resultant with 3 which gives 9.0.
Calculation of standard deviation:
Standard deviation is calculated by multiplying the number of samples with 14 and subtracting the resultant from 29 and then dividing the resulting value with 90 and taking square root which yields 1.47.
The z factor for median is calculated by dividing the difference of 10 and 9 with 1.47 which yields +0.68which is within the test statistics of ±2.00.
Hence, the results of the median run test and up/down test is random and no non randomness is detected.
d)
To determine:The results of the run test.
Introduction: Run chart refers to a line graph that displays the recorded data based on the time sequence.
d)
Answer to Problem 14P
Explanation of Solution
Given information:
| Day | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Comp. | 4 | 10 | 14 | 8 | 9 | 6 | 5 | 12 | 13 | 7 | 6 | 4 | 2 | 10 |
Formula:
Analysis of data:

To make analysis of data, the given data is compared with median (center line) to make A/B and U/D which is shown below,
Median run test:
From analysis, the observed number of runs is 8.
Calculation of expected number of runs:
The expected number of runs is calculated by adding half of the total number of samples with 1 which gives 8.
Calculation of standard deviation:
Standard deviation is calculated by subtracting number of sample 14 from 1 and dividing the resultant by 4 and taking square for the value which yields 1.80.
The z factor for median is calculated by dividing the difference of 6 and 8 with 1.80 which yields -1.11 which is beyond the test statistics of ±2.00 and non-randomness exist.
Up/Down Test:
The observed number of runs from the analysis is 7.
Calculation of expected number of runs:
The expected number of runs is calculated by subtracting the double of the number of samples 26 and subtracting from1 and dividing the resultant with 3 which gives 9.0.
Calculation of standard deviation:
Standard deviation is calculated by multiplying the number of samples with 16 and subtracting the resultant from 29 and then dividing the resulting value with 90 and taking square root which yields 1.47.
The z factor for median is calculated by dividing the difference of 7 and 9 with 1.47 which yields -1.36 which is within the test statistics of ±2.00.
Hence, the results of the median run test and up/down test is random and no non randomness is detected.
Want to see more full solutions like this?
Chapter 10 Solutions
Operations Management
- Prepare a graph of the monthly forecasts and average forecast demand for Chicago Paint Corp., a manufacturer of specialized paint for artists. Compute the demand per day for each month (round your responses to one decimal place). Month B Production Days Demand Forecast Demand per Day January 21 950 February 19 1,150 March 21 1,150 April 20 1,250 May 23 1,200 June 22 1,000' July 20 1,350 August 21 1,250 September 21 1,050 October 21 1,050 November 21 December 225 950 19 850arrow_forwardThe president of Hill Enterprises, Terri Hill, projects the firm's aggregate demand requirements over the next 8 months as follows: 2,300 January 1,500 May February 1,700 June 2,100 March April 1,700 1,700 July August 1,900 1,500 Her operations manager is considering a new plan, which begins in January with 200 units of inventory on hand. Stockout cost of lost sales is $125 per unit. Inventory holding cost is $25 per unit per month. Ignore any idle-time costs. The plan is called plan C. Plan C: Keep a stable workforce by maintaining a constant production rate equal to the average gross requirements excluding initial inventory and allow varying inventory levels. Conduct your analysis for January through August. The average monthly demand requirement = units. (Enter your response as a whole number.) In order to arrive at the costs, first compute the ending inventory and stockout units for each month by filling in the table below (enter your responses as whole numbers). Ending E Period…arrow_forwardMention four early warning indicators that a business may be at risk.arrow_forward
- 1. Define risk management and explain its importance in a small business. 2. Describe three types of risks commonly faced by entrepreneurs. 3. Explain the purpose of a risk register. 4. List and briefly describe four risk response strategies. (5 marks) (6 marks) (4 marks) (8 marks) 5. Explain how social media can pose a risk to small businesses. (5 marks) 6. Identify and describe any four hazard-based risks. (8 marks) 7. Mention four early warning indicators that a business may be at risk. (4 marks)arrow_forwardState whether each of the following statements is TRUE or FALSE. 1. Risk management involves identifying, analysing, and mitigating risks. 2. Hazard risks include interest rate fluctuations. 3. Entrepreneurs should avoid all forms of risks. 4. SWOT analysis is a tool for risk identification. 5. Scenario building helps visualise risk responses. 6. Risk appetite defines how much risk an organisation is willing to accept. 7. Diversification is a risk reduction strategy. 8. A risk management framework must align with business goals. 9. Political risk is only relevant in unstable countries. 10. All risks can be eliminated through insurance.arrow_forward9. A hazard-based risk includes A. Political instability B. Ergonomic issues C. Market demand D. Taxation changesarrow_forward
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,

