Precalculus: Mathematics for Calculus - 6th Edition
Precalculus: Mathematics for Calculus - 6th Edition
6th Edition
ISBN: 9780840068071
Author: Stewart, James, Redlin, Lothar, Watson, Saleem
Publisher: Cengage Learning
bartleby

Videos

Textbook Question
Book Icon
Chapter 10, Problem 13P

Investing in Bonds A woman wishes to invest $12,000 in three types of bonds: municipal bonds paying 7% interest per year, bank certificates paying 8%, and high-risk bonds paying 12%. For tax reasons she wants the amount invested in municipal bonds to be at least three times the amount invested in bunk certificates. To keep her level of risk manage-able, she will invest no more than $2000 in high-risk bonds. How much should she invest in each type of bond to maximize her annual interest yield? [Hint: Let x = amount in municipal bonds and y = amount in bunk certificates. Then the amount in high-risk bonds will be 12,000 − x − y.]

Expert Solution & Answer
Check Mark
To determine

To find: The amount money a women invest in the municipal bond, bank certificate bond and high-risk bond for the maximum interest.

Answer to Problem 13P

Women invest $7500 in municipal bonds, $2500 in the certificate bond and $2000 in high risk bonds.

Explanation of Solution

Given:

The total amount of money is $12000 and invest in the three types of bonds the municipal bond, bank certificate bond and high-risk bond.

The municipal bond pays 7% interest per year, bank certificate pays 8% interest per year and high risk bond pays 12% interest per year.

The amount of money a women invested in municipal bond is three times the invested in bank certificates.

Women invest no more than $2000 in high risk bonds.

Calculation:

Suppose the amount invested in the municipal bond is x and the amount invested in the bank certificate bond is y for the maximum interest.

Then the amount invested in the high risk bond is (12000−x−y) .

Use the given information to make the inequalities and the objective function for the feasible region.

The required information is shown in the table below.

municipal bond Bank certificate bond high-risk bond
Amount of money x y (12000−x−y)

The objective function is,

I=7x100+8y100+12(12000−x−y)100=12(12000−x−y)+7x+8y100=1440−5x100−4y100 ,

The constraint to get the feasible region has shown below.

x+y≥10000x+y≤12000x≥3yx≥0,y≥0}

Now, take the equalities of the above inequalities,

x+y=10000 (1)

And,

x+y=12000 (2)

And,

x=3y (3)

And,

x≥0,y≥0

Substitute 3y for x in the equation (1)

3y+y=100004y=10000y=2500

Substitute 2500 for y in equation (3),

x=3y=3⋅2500=7500

The intersection point is (x,y)=(7500,2500) .

Substitute 3y for x in the equation (2).

3y+y=120004y=12000y=3000

Substitute 3000 for y in equation (3),

x=3y=3⋅3000=9000

Now, draw the graph of the above equations,

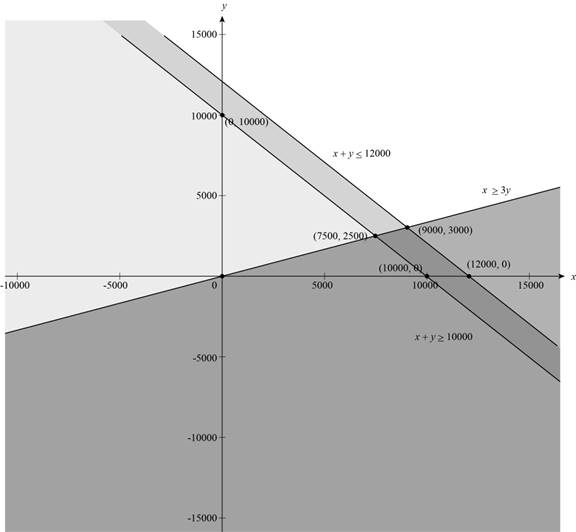
Precalculus: Mathematics for Calculus - 6th Edition, Chapter 10, Problem 13P

Figure (1)

The vertices which lies in the feasible region is shown below.

(7500,2500),(10000,0),(12000,0),(9000,3000)

Substitute the 7500 for x and 2500 for y in the objective function I=1440−5x100−4y100 ,

I=1440−5⋅7500100−4⋅2500100=1440−37500100−10000100=1440−375−100=965

Substitute the 10000 for x and 0 for y in the objective function I=1440−5x100−4y100 ,

I=1440−5⋅10000100−4⋅0100=1440−50000100=1440−500=940

Substitute the 12000 for x and 0 for y in the objective function I=1440−5x100−4y100 ,

I=1440−5⋅12000100−4⋅0100=1440−60000100=1440−600=960

Substitute the 9000 for x and 3000 for y in the objective function I=1440−5x100−4y100 ,

I=1440−5⋅9000100−4⋅3000100=1440−45000100−12000100=1440−450−120=870

So, all the satisfies these vertices are shown in the table below.

Vertices I=1440−5x100−4y100
(7500,2500) 965(Maximum)
(10000,0) 940
(9000,3000) 840
(12000,0) 960

The maximum interest rate is 965 at the investment $7500 in municipal bonds, $2500 in the certificate bond. Then the amount of money invested in high risk bond is,

12000−x−y=12000−7500−2500=12000−10000=2000

Thus, a women invest $7500 in municipal bonds, $2500 in the certificate bond and $2000 in high risk bonds at maximum interest for the objective function I=1440−5x100−4y100 .

Previous
Chapter 10, Problem 12P
Next
Chapter 10, Problem 14P

Chapter 10 Solutions

Precalculus: Mathematics for Calculus - 6th Edition

Ch. 10.1 - The system of equations {2x+3y=75xy=9 is a system...Ch. 10.1 - Prob. 2ECh. 10.1 - A system of two linear equations in two variables...Ch. 10.1 - The following is a system of two linear equations...Ch. 10.1 - Prob. 5ECh. 10.1 - Prob. 6ECh. 10.1 - Prob. 7ECh. 10.1 - Prob. 8ECh. 10.1 - Prob. 9ECh. 10.1 - Prob. 10E
Ch. 10.1 - Prob. 11ECh. 10.1 - Prob. 12ECh. 10.1 - Prob. 13ECh. 10.1 - Prob. 14ECh. 10.1 - Prob. 15ECh. 10.1 - Prob. 16ECh. 10.1 - Prob. 17ECh. 10.1 - Prob. 18ECh. 10.1 - Prob. 19ECh. 10.1 - Prob. 20ECh. 10.1 - Prob. 21ECh. 10.1 - Prob. 22ECh. 10.1 - Prob. 23ECh. 10.1 - Prob. 24ECh. 10.1 - Prob. 25ECh. 10.1 - Prob. 26ECh. 10.1 - Prob. 27ECh. 10.1 - Prob. 28ECh. 10.1 - Prob. 29ECh. 10.1 - Prob. 30ECh. 10.1 - Prob. 31ECh. 10.1 - Prob. 32ECh. 10.1 - Prob. 33ECh. 10.1 - Prob. 34ECh. 10.1 - Prob. 35ECh. 10.1 - Prob. 36ECh. 10.1 - Prob. 37ECh. 10.1 - Prob. 38ECh. 10.1 - Prob. 39ECh. 10.1 - Prob. 40ECh. 10.1 - Prob. 41ECh. 10.1 - Prob. 42ECh. 10.1 - Prob. 43ECh. 10.1 - Prob. 44ECh. 10.1 - Prob. 45ECh. 10.1 - Prob. 46ECh. 10.1 - Prob. 47ECh. 10.1 - Prob. 48ECh. 10.1 - Prob. 49ECh. 10.1 - Prob. 50ECh. 10.1 - Prob. 51ECh. 10.1 - Prob. 52ECh. 10.1 - Prob. 53ECh. 10.1 - Prob. 54ECh. 10.1 - Prob. 55ECh. 10.1 - Prob. 56ECh. 10.1 - Prob. 57ECh. 10.1 - Prob. 58ECh. 10.1 - Value of Coins A man has 14 coins in his pocket,...Ch. 10.1 - Admission Fees The admission fee at an amusement...Ch. 10.1 - Gas Station A gas station sells regular gas for...Ch. 10.1 - Fruit Stand A fruit stand sells two varieties of...Ch. 10.1 - Airplane Speed A man flies a small airplane from...Ch. 10.1 - Boat Speed A boat on a river travels downstream...Ch. 10.1 - Nutrition A researcher performs an experiment to...Ch. 10.1 - Coffee Blends A customer in a coffee shop...Ch. 10.1 - Mixture Problem A chemist has two large containers...Ch. 10.1 - Mixture Problem A biologist has two brine...Ch. 10.1 - Investments A woman invests a total of 20,000 in...Ch. 10.1 - Investments A man invests his savings in two...Ch. 10.1 - Prob. 71ECh. 10.1 - Prob. 72ECh. 10.1 - Prob. 73ECh. 10.1 - Area of a Triangle Find the area of the triangle...Ch. 10.1 - Prob. 75ECh. 10.2 - These exercises refer to the following system:...Ch. 10.2 - Prob. 2ECh. 10.2 - Prob. 3ECh. 10.2 - Prob. 4ECh. 10.2 - Prob. 5ECh. 10.2 - Prob. 6ECh. 10.2 - Prob. 7ECh. 10.2 - Prob. 8ECh. 10.2 - Prob. 9ECh. 10.2 - Prob. 10ECh. 10.2 - Prob. 11ECh. 10.2 - Prob. 12ECh. 10.2 - Prob. 13ECh. 10.2 - Prob. 14ECh. 10.2 - Prob. 15ECh. 10.2 - Prob. 16ECh. 10.2 - Prob. 17ECh. 10.2 - Prob. 18ECh. 10.2 - Prob. 19ECh. 10.2 - Prob. 20ECh. 10.2 - Prob. 21ECh. 10.2 - Prob. 22ECh. 10.2 - Prob. 23ECh. 10.2 - Prob. 24ECh. 10.2 - Prob. 25ECh. 10.2 - Prob. 26ECh. 10.2 - Prob. 27ECh. 10.2 - Prob. 28ECh. 10.2 - Prob. 29ECh. 10.2 - Prob. 30ECh. 10.2 - Prob. 31ECh. 10.2 - Prob. 32ECh. 10.2 - Prob. 33ECh. 10.2 - Prob. 34ECh. 10.2 - Prob. 35ECh. 10.2 - Prob. 36ECh. 10.2 - Prob. 37ECh. 10.2 - Prob. 38ECh. 10.2 - Prob. 39ECh. 10.2 - Gas Station A gas station sells three types of...Ch. 10.2 - Nutrition A biologist is performing an experiment...Ch. 10.2 - Diet Program Nicole started a new diet that...Ch. 10.2 - Juice Blends The Juice Company offers three kinds...Ch. 10.2 - Appliance Manufacturing Kitchen Korner produces...Ch. 10.2 - Stock Portfolio An investor owns three stocks: A,...Ch. 10.2 - Electricity By using Kirchhoffs Laws, it can be...Ch. 10.2 - Prob. 47ECh. 10.3 - If a system of linear equations has infinitely...Ch. 10.3 - Prob. 2ECh. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Prob. 7ECh. 10.3 - Prob. 8ECh. 10.3 - Prob. 9ECh. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Prob. 12ECh. 10.3 - Prob. 13ECh. 10.3 - Prob. 14ECh. 10.3 - Prob. 15ECh. 10.3 - Prob. 16ECh. 10.3 - Prob. 17ECh. 10.3 - Prob. 18ECh. 10.3 - Prob. 19ECh. 10.3 - Prob. 20ECh. 10.3 - Prob. 21ECh. 10.3 - Prob. 22ECh. 10.3 - Prob. 23ECh. 10.3 - Prob. 24ECh. 10.3 - Prob. 25ECh. 10.3 - Prob. 26ECh. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Prob. 29ECh. 10.3 - Prob. 30ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 32ECh. 10.3 - Prob. 33ECh. 10.3 - Prob. 34ECh. 10.3 - Prob. 35ECh. 10.3 - Prob. 36ECh. 10.3 - Prob. 37ECh. 10.3 - Prob. 38ECh. 10.3 - Prob. 39ECh. 10.3 - Prob. 40ECh. 10.3 - Prob. 41ECh. 10.3 - Prob. 42ECh. 10.3 - Prob. 43ECh. 10.3 - Prob. 44ECh. 10.3 - Prob. 45ECh. 10.3 - Prob. 46ECh. 10.3 - Prob. 47ECh. 10.3 - Prob. 48ECh. 10.3 - Prob. 49ECh. 10.3 - Prob. 50ECh. 10.3 - Prob. 51ECh. 10.3 - Prob. 52ECh. 10.3 - Prob. 53ECh. 10.3 - Prob. 54ECh. 10.3 - Nutrition A doctor recommends that a patient take...Ch. 10.3 - Mixtures A chemist has three acid solutions at...Ch. 10.3 - Distance, Speed, and Time Amanda, Bryce, and Corey...Ch. 10.3 - Classroom Use A small school has 100 students who...Ch. 10.3 - Manufacturing Furniture A furniture factory makes...Ch. 10.3 - Traffic Flow A section of a citys street network...Ch. 10.3 - Prob. 61ECh. 10.4 - We can add (or subtract) two matrices only if they...Ch. 10.4 - (a) We can multiply two matrices only if the...Ch. 10.4 - Prob. 3ECh. 10.4 - Fill in the missing entries in the product matrix....Ch. 10.4 - Prob. 5ECh. 10.4 - Prob. 6ECh. 10.4 - Prob. 7ECh. 10.4 - Prob. 8ECh. 10.4 - Prob. 9ECh. 10.4 - Prob. 10ECh. 10.4 - Prob. 11ECh. 10.4 - Prob. 12ECh. 10.4 - Prob. 13ECh. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Prob. 17ECh. 10.4 - Prob. 18ECh. 10.4 - Prob. 19ECh. 10.4 - Prob. 20ECh. 10.4 - Prob. 21ECh. 10.4 - Prob. 22ECh. 10.4 - Prob. 23ECh. 10.4 - Prob. 24ECh. 10.4 - Prob. 25ECh. 10.4 - Prob. 26ECh. 10.4 - Prob. 27ECh. 10.4 - Prob. 28ECh. 10.4 - Prob. 29ECh. 10.4 - Prob. 30ECh. 10.4 - Prob. 31ECh. 10.4 - Prob. 32ECh. 10.4 - Prob. 33ECh. 10.4 - Prob. 34ECh. 10.4 - Prob. 35ECh. 10.4 - Prob. 36ECh. 10.4 - Prob. 37ECh. 10.4 - Prob. 38ECh. 10.4 - Prob. 39ECh. 10.4 - Prob. 40ECh. 10.4 - Prob. 41ECh. 10.4 - Prob. 42ECh. 10.4 - Prob. 43ECh. 10.4 - Prob. 44ECh. 10.4 - Fast-Food Sales A small fast-food chain with...Ch. 10.4 - Prob. 46ECh. 10.4 - Canning Tomato Products Jaeger Foods produces...Ch. 10.4 - Produce Sales A farmers three children, Amy, Beth,...Ch. 10.4 - Digital Images A four-level gray scale is shown...Ch. 10.4 - Prob. 50ECh. 10.4 - Prob. 51ECh. 10.4 - Prob. 52ECh. 10.4 - Prob. 53ECh. 10.5 - (a) The matrix I=[1001] is called an __________...Ch. 10.5 - Prob. 2ECh. 10.5 - Prob. 3ECh. 10.5 - Prob. 4ECh. 10.5 - Prob. 5ECh. 10.5 - Prob. 6ECh. 10.5 - Prob. 7ECh. 10.5 - Prob. 8ECh. 10.5 - Prob. 9ECh. 10.5 - Prob. 10ECh. 10.5 - Prob. 11ECh. 10.5 - Prob. 12ECh. 10.5 - Prob. 13ECh. 10.5 - Prob. 14ECh. 10.5 - Prob. 15ECh. 10.5 - Prob. 16ECh. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - Prob. 20ECh. 10.5 - Prob. 21ECh. 10.5 - Prob. 22ECh. 10.5 - Prob. 23ECh. 10.5 - Prob. 24ECh. 10.5 - Prob. 25ECh. 10.5 - Prob. 26ECh. 10.5 - Prob. 27ECh. 10.5 - Prob. 28ECh. 10.5 - Prob. 29ECh. 10.5 - Prob. 30ECh. 10.5 - Prob. 31ECh. 10.5 - Prob. 32ECh. 10.5 - Prob. 33ECh. 10.5 - Prob. 34ECh. 10.5 - Prob. 35ECh. 10.5 - Prob. 36ECh. 10.5 - Prob. 37ECh. 10.5 - Prob. 38ECh. 10.5 - Prob. 39ECh. 10.5 - Prob. 40ECh. 10.5 - Prob. 41ECh. 10.5 - Prob. 42ECh. 10.5 - Prob. 43ECh. 10.5 - Prob. 44ECh. 10.5 - Prob. 45ECh. 10.5 - Prob. 46ECh. 10.5 - Nutrition A nutritionist is studying the effects...Ch. 10.5 - Prob. 48ECh. 10.5 - Prob. 49ECh. 10.5 - Prob. 50ECh. 10.6 - True or false? det(A) is defined only for a square...Ch. 10.6 - Prob. 2ECh. 10.6 - True or false? If det(A) = 0, then A is not...Ch. 10.6 - Prob. 4ECh. 10.6 - Prob. 5ECh. 10.6 - Prob. 6ECh. 10.6 - Prob. 7ECh. 10.6 - Prob. 8ECh. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - Prob. 11ECh. 10.6 - Prob. 12ECh. 10.6 - Prob. 13ECh. 10.6 - Prob. 14ECh. 10.6 - Prob. 15ECh. 10.6 - Prob. 16ECh. 10.6 - Prob. 17ECh. 10.6 - Prob. 18ECh. 10.6 - Prob. 19ECh. 10.6 - Prob. 20ECh. 10.6 - Prob. 21ECh. 10.6 - Prob. 22ECh. 10.6 - Prob. 23ECh. 10.6 - Prob. 24ECh. 10.6 - Prob. 25ECh. 10.6 - Prob. 26ECh. 10.6 - Prob. 27ECh. 10.6 - Prob. 28ECh. 10.6 - Prob. 29ECh. 10.6 - Prob. 30ECh. 10.6 - Prob. 31ECh. 10.6 - Prob. 32ECh. 10.6 - Prob. 33ECh. 10.6 - Prob. 34ECh. 10.6 - Prob. 35ECh. 10.6 - Prob. 36ECh. 10.6 - Prob. 37ECh. 10.6 - Prob. 38ECh. 10.6 - Prob. 39ECh. 10.6 - Prob. 40ECh. 10.6 - Prob. 41ECh. 10.6 - Prob. 42ECh. 10.6 - Prob. 43ECh. 10.6 - Prob. 44ECh. 10.6 - Prob. 45ECh. 10.6 - Prob. 46ECh. 10.6 - Prob. 47ECh. 10.6 - Prob. 48ECh. 10.6 - Prob. 49ECh. 10.6 - Prob. 50ECh. 10.6 - Prob. 51ECh. 10.6 - Prob. 52ECh. 10.6 - Prob. 53ECh. 10.6 - Prob. 54ECh. 10.6 - Prob. 55ECh. 10.6 - Prob. 56ECh. 10.6 - Prob. 57ECh. 10.6 - Prob. 58ECh. 10.6 - Prob. 59ECh. 10.6 - Prob. 60ECh. 10.6 - The Arch of a Bridge The opening of a railway...Ch. 10.6 - A Triangular Plot of Land An outdoors club is...Ch. 10.6 - Prob. 63ECh. 10.6 - Prob. 64ECh. 10.6 - Prob. 65ECh. 10.6 - Prob. 66ECh. 10.6 - Prob. 67ECh. 10.7 - For each rational function r, choose from (i)(iv)...Ch. 10.7 - Prob. 2ECh. 10.7 - Prob. 3ECh. 10.7 - Prob. 4ECh. 10.7 - Prob. 5ECh. 10.7 - Prob. 6ECh. 10.7 - Prob. 7ECh. 10.7 - Prob. 8ECh. 10.7 - Prob. 9ECh. 10.7 - Prob. 10ECh. 10.7 - Prob. 11ECh. 10.7 - Prob. 12ECh. 10.7 - Prob. 13ECh. 10.7 - Prob. 14ECh. 10.7 - Prob. 15ECh. 10.7 - Prob. 16ECh. 10.7 - Prob. 17ECh. 10.7 - Prob. 18ECh. 10.7 - Prob. 19ECh. 10.7 - Prob. 20ECh. 10.7 - Prob. 21ECh. 10.7 - Prob. 22ECh. 10.7 - Prob. 23ECh. 10.7 - Prob. 24ECh. 10.7 - Prob. 25ECh. 10.7 - Prob. 26ECh. 10.7 - Prob. 27ECh. 10.7 - Prob. 28ECh. 10.7 - Prob. 29ECh. 10.7 - Prob. 30ECh. 10.7 - Prob. 31ECh. 10.7 - Prob. 32ECh. 10.7 - Prob. 33ECh. 10.7 - Prob. 34ECh. 10.7 - Prob. 35ECh. 10.7 - Prob. 36ECh. 10.7 - Prob. 37ECh. 10.7 - Prob. 38ECh. 10.7 - Prob. 39ECh. 10.7 - Prob. 40ECh. 10.7 - Prob. 41ECh. 10.7 - Prob. 42ECh. 10.7 - Prob. 43ECh. 10.7 - Prob. 44ECh. 10.7 - Prob. 45ECh. 10.7 - Prob. 46ECh. 10.7 - Prob. 47ECh. 10.7 - Prob. 48ECh. 10.8 - The system of equations {2yx2=0yx=4 is graphed...Ch. 10.8 - Prob. 2ECh. 10.8 - Prob. 3ECh. 10.8 - Prob. 4ECh. 10.8 - Prob. 5ECh. 10.8 - Prob. 6ECh. 10.8 - Prob. 7ECh. 10.8 - Prob. 8ECh. 10.8 - Prob. 9ECh. 10.8 - Prob. 10ECh. 10.8 - Prob. 11ECh. 10.8 - Prob. 12ECh. 10.8 - Prob. 13ECh. 10.8 - Prob. 14ECh. 10.8 - Prob. 15ECh. 10.8 - Prob. 16ECh. 10.8 - Prob. 17ECh. 10.8 - Prob. 18ECh. 10.8 - Prob. 19ECh. 10.8 - Prob. 20ECh. 10.8 - Prob. 21ECh. 10.8 - Prob. 22ECh. 10.8 - Prob. 23ECh. 10.8 - Prob. 24ECh. 10.8 - Prob. 25ECh. 10.8 - Prob. 26ECh. 10.8 - Prob. 27ECh. 10.8 - Prob. 28ECh. 10.8 - Prob. 29ECh. 10.8 - Prob. 30ECh. 10.8 - Prob. 31ECh. 10.8 - Prob. 32ECh. 10.8 - Prob. 33ECh. 10.8 - Prob. 34ECh. 10.8 - Prob. 35ECh. 10.8 - Prob. 36ECh. 10.8 - Prob. 37ECh. 10.8 - Prob. 38ECh. 10.8 - Prob. 39ECh. 10.8 - Prob. 40ECh. 10.8 - Dimensions of a Rectangle A rectangle has an area...Ch. 10.8 - Legs of a Right Triangle A right triangle has an...Ch. 10.8 - Dimensions of a Rectangle The perimeter of a...Ch. 10.8 - Dimensions of a Rectangle A circular piece of...Ch. 10.8 - Flight of a Rocket A hill is inclined so that its...Ch. 10.8 - Making a Stovepipe A rectangular piece of sheet...Ch. 10.8 - Global Positioning System (GPS) The Global...Ch. 10.8 - Prob. 48ECh. 10.8 - Prob. 49ECh. 10.9 - To graph an inequality, we first graph the...Ch. 10.9 - Prob. 2ECh. 10.9 - Prob. 3ECh. 10.9 - Prob. 4ECh. 10.9 - Prob. 5ECh. 10.9 - Prob. 6ECh. 10.9 - Prob. 7ECh. 10.9 - Prob. 8ECh. 10.9 - Prob. 9ECh. 10.9 - Prob. 10ECh. 10.9 - Prob. 11ECh. 10.9 - Prob. 12ECh. 10.9 - Prob. 13ECh. 10.9 - Prob. 14ECh. 10.9 - Prob. 15ECh. 10.9 - Prob. 16ECh. 10.9 - Prob. 17ECh. 10.9 - Prob. 18ECh. 10.9 - Prob. 19ECh. 10.9 - Prob. 20ECh. 10.9 - Prob. 21ECh. 10.9 - Prob. 22ECh. 10.9 - Prob. 23ECh. 10.9 - Prob. 24ECh. 10.9 - Prob. 25ECh. 10.9 - Prob. 26ECh. 10.9 - Prob. 27ECh. 10.9 - Prob. 28ECh. 10.9 - Prob. 29ECh. 10.9 - Prob. 30ECh. 10.9 - Prob. 31ECh. 10.9 - Prob. 32ECh. 10.9 - Prob. 33ECh. 10.9 - Prob. 34ECh. 10.9 - Prob. 35ECh. 10.9 - Prob. 36ECh. 10.9 - Prob. 37ECh. 10.9 - Prob. 38ECh. 10.9 - Prob. 39ECh. 10.9 - Prob. 40ECh. 10.9 - Prob. 41ECh. 10.9 - Prob. 42ECh. 10.9 - Prob. 43ECh. 10.9 - Prob. 44ECh. 10.9 - Prob. 45ECh. 10.9 - Prob. 46ECh. 10.9 - Prob. 47ECh. 10.9 - Prob. 48ECh. 10.9 - Prob. 49ECh. 10.9 - Prob. 50ECh. 10.9 - Prob. 51ECh. 10.9 - Prob. 52ECh. 10.9 - Coffee Blends A coffee merchant sells two...Ch. 10.9 - Nutrition A cat food manufacturer uses fish and...Ch. 10.9 - Prob. 55ECh. 10 - Prob. 1RCCCh. 10 - Prob. 2RCCCh. 10 - Prob. 3RCCCh. 10 - Prob. 4RCCCh. 10 - Prob. 5RCCCh. 10 - Prob. 6RCCCh. 10 - Prob. 7RCCCh. 10 - Prob. 8RCCCh. 10 - Prob. 9RCCCh. 10 - Prob. 10RCCCh. 10 - Prob. 11RCCCh. 10 - Prob. 12RCCCh. 10 - Prob. 13RCCCh. 10 - Prob. 14RCCCh. 10 - Prob. 15RCCCh. 10 - Prob. 16RCCCh. 10 - Prob. 17RCCCh. 10 - Prob. 18RCCCh. 10 - Prob. 19RCCCh. 10 - Prob. 1RECh. 10 - Prob. 2RECh. 10 - Prob. 3RECh. 10 - Prob. 4RECh. 10 - Prob. 5RECh. 10 - Prob. 6RECh. 10 - Prob. 7RECh. 10 - Prob. 8RECh. 10 - Prob. 9RECh. 10 - Prob. 10RECh. 10 - Prob. 11RECh. 10 - Prob. 12RECh. 10 - Prob. 13RECh. 10 - Prob. 14RECh. 10 - Prob. 15RECh. 10 - Prob. 16RECh. 10 - Prob. 17RECh. 10 - Prob. 18RECh. 10 - Prob. 19RECh. 10 - Prob. 20RECh. 10 - Prob. 21RECh. 10 - Prob. 22RECh. 10 - Prob. 23RECh. 10 - Prob. 24RECh. 10 - Prob. 25RECh. 10 - Prob. 26RECh. 10 - Prob. 27RECh. 10 - Prob. 28RECh. 10 - Prob. 29RECh. 10 - Prob. 30RECh. 10 - Prob. 31RECh. 10 - Prob. 32RECh. 10 - Prob. 33RECh. 10 - Prob. 34RECh. 10 - Prob. 35RECh. 10 - Prob. 36RECh. 10 - Prob. 37RECh. 10 - Prob. 38RECh. 10 - Prob. 39RECh. 10 - Prob. 40RECh. 10 - Prob. 41RECh. 10 - Prob. 42RECh. 10 - Prob. 43RECh. 10 - Prob. 44RECh. 10 - Prob. 45RECh. 10 - Prob. 46RECh. 10 - Prob. 47RECh. 10 - Prob. 48RECh. 10 - Prob. 49RECh. 10 - Prob. 50RECh. 10 - Prob. 51RECh. 10 - Prob. 52RECh. 10 - Prob. 53RECh. 10 - Prob. 54RECh. 10 - Prob. 55RECh. 10 - Prob. 56RECh. 10 - Prob. 57RECh. 10 - Prob. 58RECh. 10 - Prob. 59RECh. 10 - Prob. 60RECh. 10 - Prob. 61RECh. 10 - Prob. 62RECh. 10 - Prob. 63RECh. 10 - Prob. 64RECh. 10 - Prob. 65RECh. 10 - Prob. 66RECh. 10 - Prob. 67RECh. 10 - Prob. 68RECh. 10 - Prob. 69RECh. 10 - Prob. 70RECh. 10 - Prob. 71RECh. 10 - Prob. 72RECh. 10 - Prob. 73RECh. 10 - Prob. 74RECh. 10 - Prob. 75RECh. 10 - Prob. 76RECh. 10 - Prob. 77RECh. 10 - Prob. 78RECh. 10 - Prob. 79RECh. 10 - Prob. 80RECh. 10 - Prob. 81RECh. 10 - Prob. 82RECh. 10 - Prob. 83RECh. 10 - Prob. 84RECh. 10 - Prob. 85RECh. 10 - Prob. 86RECh. 10 - Prob. 87RECh. 10 - Prob. 88RECh. 10 - Prob. 89RECh. 10 - Prob. 90RECh. 10 - Prob. 91RECh. 10 - Prob. 92RECh. 10 - Prob. 93RECh. 10 - Prob. 94RECh. 10 - Prob. 95RECh. 10 - Prob. 96RECh. 10 - Prob. 97RECh. 10 - Prob. 98RECh. 10 - Prob. 99RECh. 10 - Prob. 100RECh. 10 - Prob. 101RECh. 10 - Prob. 102RECh. 10 - Prob. 103RECh. 10 - Prob. 104RECh. 10 - Prob. 105RECh. 10 - Prob. 106RECh. 10 - Prob. 107RECh. 10 - Prob. 108RECh. 10 - Prob. 109RECh. 10 - Prob. 110RECh. 10 - Prob. 111RECh. 10 - Prob. 112RECh. 10 - Prob. 1TCh. 10 - Prob. 2TCh. 10 - Prob. 3TCh. 10 - Prob. 4TCh. 10 - Prob. 5TCh. 10 - Prob. 6TCh. 10 - Prob. 7TCh. 10 - Anne, Barry, and Cathy enter a coffee shop. Anne...Ch. 10 - Prob. 9TCh. 10 - Prob. 10TCh. 10 - Only one of the following matrices has an inverse....Ch. 10 - Prob. 12TCh. 10 - Prob. 13TCh. 10 - Prob. 14TCh. 10 - Find the maximum and minimum values of the given...Ch. 10 - Prob. 2PCh. 10 - Prob. 3PCh. 10 - Find the maximum and minimum value of the given...Ch. 10 - Making Furniture A furniture manufacturer makes...Ch. 10 - A Housing Development A housing contractor has...Ch. 10 - Hauling Fruit A trucker hauls citrus fruit from...Ch. 10 - Manufacturing Calculators A manufacturer of...Ch. 10 - Shipping Televisions An electronics discount chain...Ch. 10 - Prob. 10PCh. 10 - Packaging Nuts A confectioner sells two types of...Ch. 10 - Feeding Lab Rabbits A biologist wishes to feed...Ch. 10 - Investing in Bonds A woman wishes to invest 12,000...Ch. 10 - Prob. 14PCh. 10 - Business Strategy A small software company...Ch. 10 - Feasible Region All parts of this problem refer to...
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Solve ANY Optimization Problem in 5 Steps w/ Examples. What are they and How do you solve them?; Author: Ace Tutors;https://www.youtube.com/watch?v=BfOSKc_sncg;License: Standard YouTube License, CC-BY
Types of solution in LPP|Basic|Multiple solution|Unbounded|Infeasible|GTU|Special case of LP problem; Author: Mechanical Engineering Management;https://www.youtube.com/watch?v=F-D2WICq8Sk;License: Standard YouTube License, CC-BY
Optimization Problems in Calculus; Author: Professor Dave Explains;https://www.youtube.com/watch?v=q1U6AmIa_uQ;License: Standard YouTube License, CC-BY
Introduction to Optimization; Author: Math with Dr. Claire;https://www.youtube.com/watch?v=YLzgYm2tN8E;License: Standard YouTube License, CC-BY