Precalculus: Mathematics for Calculus - 6th Edition
6th Edition
ISBN: 9780840068071
Author: Stewart, James, Redlin, Lothar, Watson, Saleem
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 10, Problem 1RCC
(a)
To determine
The system of equation need to solve by using the substitution method is to be described.
(a)
Expert Solution
Answer to Problem 1RCC
Substitution method is nothing but a method to solve the value of one variable with the help of another variable of system of equation.
Explanation of Solution
If in the system of equations, there are two variables are used and they said that need to solve the system of equations with the help of the substitution method then one need to rewrite the one equation out of two to get one variable value.
Then put this variable value into the second eq. then the new eq. will find which is used to find another value of second variable. Now, you will get the exact value of the second variable, use it to find the first variable.
For example:
The given eqns. are:
Put the value of
Now, to find the value of
So, the solutions of given set of eqns. is
Conclusion:
Hence, the solutions of given set of eqns. is well described with the substitution method.
(b)
To determine
The system of equation need to solve by using the elimination method is to be described.
(b)
Expert Solution
Answer to Problem 1RCC
You have to use either addition or subtraction to find the value of one variable and then use this value of one variable to get value of another variable in the elimination method.
Explanation of Solution
If in the system of equations, there are two variables are used and they said that need to solve the system of equations with the help of the elimination method thenyou have to use either addition or subtraction to find the value of one variable.
Then use this value of one variable to get value of another variable in the elimination method for the given system of equations.
For example:
The given eqns. are:
Multiply by
Take the subtraction of eqns. (3) and (2):
Now, to find the value of
So, the solutions of given set of eqns. is
Conclusion:
Hence, the solutions of given set of eqns. is well described with the elimination method.
(c)
To determine
The system of equation need to solve by using the graphical method is to be described.
(c)
Expert Solution
Answer to Problem 1RCC
Graph both equations using either pencil-paper or graphing calculator in the same co-ordinate plane, the intersection point of the equations is nothing but the solution of the system of equation.
Explanation of Solution
If the system of two equations needs to solve by the graphically method then firstly need to write the given equations in the form of slope intercept.
The slope intercept form is given as:
Where,
Slope:
After that; just draw the graphs of equation by using the graphing calculator or paper −pencil based on your choice.
Now the cases of solution in the graphically method is as:
When the graph line of two equations intersects at a point then one can say that the system of eq. has one solution.
When the graph line of two equations is parallel then one can say that the system of eq. has no solution.
When the graph line of two equations is same then one can say that the system of eq. has infinitely much solution.
For example:
The given eqns. are:
Need to write the given eq. in the slope intercept form:
Since the slopes are different, the lines must intersect at a point. Here are the graphs of the both eqns:
So, the given set of system has one solution as
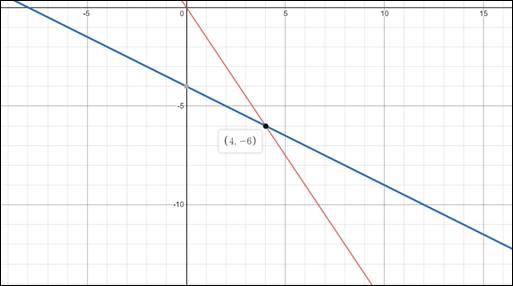
Conclusion:
Hence, the solutions of given set of eqns. is well described with the graphical method.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Chapter 10 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
Ch. 10.1 - The system of equations {2x+3y=75xy=9 is a system...Ch. 10.1 - Prob. 2ECh. 10.1 - A system of two linear equations in two variables...Ch. 10.1 - The following is a system of two linear equations...Ch. 10.1 - Prob. 5ECh. 10.1 - Prob. 6ECh. 10.1 - Prob. 7ECh. 10.1 - Prob. 8ECh. 10.1 - Prob. 9ECh. 10.1 - Prob. 10E
Ch. 10.1 - Prob. 11ECh. 10.1 - Prob. 12ECh. 10.1 - Prob. 13ECh. 10.1 - Prob. 14ECh. 10.1 - Prob. 15ECh. 10.1 - Prob. 16ECh. 10.1 - Prob. 17ECh. 10.1 - Prob. 18ECh. 10.1 - Prob. 19ECh. 10.1 - Prob. 20ECh. 10.1 - Prob. 21ECh. 10.1 - Prob. 22ECh. 10.1 - Prob. 23ECh. 10.1 - Prob. 24ECh. 10.1 - Prob. 25ECh. 10.1 - Prob. 26ECh. 10.1 - Prob. 27ECh. 10.1 - Prob. 28ECh. 10.1 - Prob. 29ECh. 10.1 - Prob. 30ECh. 10.1 - Prob. 31ECh. 10.1 - Prob. 32ECh. 10.1 - Prob. 33ECh. 10.1 - Prob. 34ECh. 10.1 - Prob. 35ECh. 10.1 - Prob. 36ECh. 10.1 - Prob. 37ECh. 10.1 - Prob. 38ECh. 10.1 - Prob. 39ECh. 10.1 - Prob. 40ECh. 10.1 - Prob. 41ECh. 10.1 - Prob. 42ECh. 10.1 - Prob. 43ECh. 10.1 - Prob. 44ECh. 10.1 - Prob. 45ECh. 10.1 - Prob. 46ECh. 10.1 - Prob. 47ECh. 10.1 - Prob. 48ECh. 10.1 - Prob. 49ECh. 10.1 - Prob. 50ECh. 10.1 - Prob. 51ECh. 10.1 - Prob. 52ECh. 10.1 - Prob. 53ECh. 10.1 - Prob. 54ECh. 10.1 - Prob. 55ECh. 10.1 - Prob. 56ECh. 10.1 - Prob. 57ECh. 10.1 - Prob. 58ECh. 10.1 - Value of Coins A man has 14 coins in his pocket,...Ch. 10.1 - Admission Fees The admission fee at an amusement...Ch. 10.1 - Gas Station A gas station sells regular gas for...Ch. 10.1 - Fruit Stand A fruit stand sells two varieties of...Ch. 10.1 - Airplane Speed A man flies a small airplane from...Ch. 10.1 - Boat Speed A boat on a river travels downstream...Ch. 10.1 - Nutrition A researcher performs an experiment to...Ch. 10.1 - Coffee Blends A customer in a coffee shop...Ch. 10.1 - Mixture Problem A chemist has two large containers...Ch. 10.1 - Mixture Problem A biologist has two brine...Ch. 10.1 - Investments A woman invests a total of 20,000 in...Ch. 10.1 - Investments A man invests his savings in two...Ch. 10.1 - Prob. 71ECh. 10.1 - Prob. 72ECh. 10.1 - Prob. 73ECh. 10.1 - Area of a Triangle Find the area of the triangle...Ch. 10.1 - Prob. 75ECh. 10.2 - These exercises refer to the following system:...Ch. 10.2 - Prob. 2ECh. 10.2 - Prob. 3ECh. 10.2 - Prob. 4ECh. 10.2 - Prob. 5ECh. 10.2 - Prob. 6ECh. 10.2 - Prob. 7ECh. 10.2 - Prob. 8ECh. 10.2 - Prob. 9ECh. 10.2 - Prob. 10ECh. 10.2 - Prob. 11ECh. 10.2 - Prob. 12ECh. 10.2 - Prob. 13ECh. 10.2 - Prob. 14ECh. 10.2 - Prob. 15ECh. 10.2 - Prob. 16ECh. 10.2 - Prob. 17ECh. 10.2 - Prob. 18ECh. 10.2 - Prob. 19ECh. 10.2 - Prob. 20ECh. 10.2 - Prob. 21ECh. 10.2 - Prob. 22ECh. 10.2 - Prob. 23ECh. 10.2 - Prob. 24ECh. 10.2 - Prob. 25ECh. 10.2 - Prob. 26ECh. 10.2 - Prob. 27ECh. 10.2 - Prob. 28ECh. 10.2 - Prob. 29ECh. 10.2 - Prob. 30ECh. 10.2 - Prob. 31ECh. 10.2 - Prob. 32ECh. 10.2 - Prob. 33ECh. 10.2 - Prob. 34ECh. 10.2 - Prob. 35ECh. 10.2 - Prob. 36ECh. 10.2 - Prob. 37ECh. 10.2 - Prob. 38ECh. 10.2 - Prob. 39ECh. 10.2 - Gas Station A gas station sells three types of...Ch. 10.2 - Nutrition A biologist is performing an experiment...Ch. 10.2 - Diet Program Nicole started a new diet that...Ch. 10.2 - Juice Blends The Juice Company offers three kinds...Ch. 10.2 - Appliance Manufacturing Kitchen Korner produces...Ch. 10.2 - Stock Portfolio An investor owns three stocks: A,...Ch. 10.2 - Electricity By using Kirchhoffs Laws, it can be...Ch. 10.2 - Prob. 47ECh. 10.3 - If a system of linear equations has infinitely...Ch. 10.3 - Prob. 2ECh. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Prob. 7ECh. 10.3 - Prob. 8ECh. 10.3 - Prob. 9ECh. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Prob. 12ECh. 10.3 - Prob. 13ECh. 10.3 - Prob. 14ECh. 10.3 - Prob. 15ECh. 10.3 - Prob. 16ECh. 10.3 - Prob. 17ECh. 10.3 - Prob. 18ECh. 10.3 - Prob. 19ECh. 10.3 - Prob. 20ECh. 10.3 - Prob. 21ECh. 10.3 - Prob. 22ECh. 10.3 - Prob. 23ECh. 10.3 - Prob. 24ECh. 10.3 - Prob. 25ECh. 10.3 - Prob. 26ECh. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Prob. 29ECh. 10.3 - Prob. 30ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 32ECh. 10.3 - Prob. 33ECh. 10.3 - Prob. 34ECh. 10.3 - Prob. 35ECh. 10.3 - Prob. 36ECh. 10.3 - Prob. 37ECh. 10.3 - Prob. 38ECh. 10.3 - Prob. 39ECh. 10.3 - Prob. 40ECh. 10.3 - Prob. 41ECh. 10.3 - Prob. 42ECh. 10.3 - Prob. 43ECh. 10.3 - Prob. 44ECh. 10.3 - Prob. 45ECh. 10.3 - Prob. 46ECh. 10.3 - Prob. 47ECh. 10.3 - Prob. 48ECh. 10.3 - Prob. 49ECh. 10.3 - Prob. 50ECh. 10.3 - Prob. 51ECh. 10.3 - Prob. 52ECh. 10.3 - Prob. 53ECh. 10.3 - Prob. 54ECh. 10.3 - Nutrition A doctor recommends that a patient take...Ch. 10.3 - Mixtures A chemist has three acid solutions at...Ch. 10.3 - Distance, Speed, and Time Amanda, Bryce, and Corey...Ch. 10.3 - Classroom Use A small school has 100 students who...Ch. 10.3 - Manufacturing Furniture A furniture factory makes...Ch. 10.3 - Traffic Flow A section of a citys street network...Ch. 10.3 - Prob. 61ECh. 10.4 - We can add (or subtract) two matrices only if they...Ch. 10.4 - (a) We can multiply two matrices only if the...Ch. 10.4 - Prob. 3ECh. 10.4 - Fill in the missing entries in the product matrix....Ch. 10.4 - Prob. 5ECh. 10.4 - Prob. 6ECh. 10.4 - Prob. 7ECh. 10.4 - Prob. 8ECh. 10.4 - Prob. 9ECh. 10.4 - Prob. 10ECh. 10.4 - Prob. 11ECh. 10.4 - Prob. 12ECh. 10.4 - Prob. 13ECh. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Prob. 17ECh. 10.4 - Prob. 18ECh. 10.4 - Prob. 19ECh. 10.4 - Prob. 20ECh. 10.4 - Prob. 21ECh. 10.4 - Prob. 22ECh. 10.4 - Prob. 23ECh. 10.4 - Prob. 24ECh. 10.4 - Prob. 25ECh. 10.4 - Prob. 26ECh. 10.4 - Prob. 27ECh. 10.4 - Prob. 28ECh. 10.4 - Prob. 29ECh. 10.4 - Prob. 30ECh. 10.4 - Prob. 31ECh. 10.4 - Prob. 32ECh. 10.4 - Prob. 33ECh. 10.4 - Prob. 34ECh. 10.4 - Prob. 35ECh. 10.4 - Prob. 36ECh. 10.4 - Prob. 37ECh. 10.4 - Prob. 38ECh. 10.4 - Prob. 39ECh. 10.4 - Prob. 40ECh. 10.4 - Prob. 41ECh. 10.4 - Prob. 42ECh. 10.4 - Prob. 43ECh. 10.4 - Prob. 44ECh. 10.4 - Fast-Food Sales A small fast-food chain with...Ch. 10.4 - Prob. 46ECh. 10.4 - Canning Tomato Products Jaeger Foods produces...Ch. 10.4 - Produce Sales A farmers three children, Amy, Beth,...Ch. 10.4 - Digital Images A four-level gray scale is shown...Ch. 10.4 - Prob. 50ECh. 10.4 - Prob. 51ECh. 10.4 - Prob. 52ECh. 10.4 - Prob. 53ECh. 10.5 - (a) The matrix I=[1001] is called an __________...Ch. 10.5 - Prob. 2ECh. 10.5 - Prob. 3ECh. 10.5 - Prob. 4ECh. 10.5 - Prob. 5ECh. 10.5 - Prob. 6ECh. 10.5 - Prob. 7ECh. 10.5 - Prob. 8ECh. 10.5 - Prob. 9ECh. 10.5 - Prob. 10ECh. 10.5 - Prob. 11ECh. 10.5 - Prob. 12ECh. 10.5 - Prob. 13ECh. 10.5 - Prob. 14ECh. 10.5 - Prob. 15ECh. 10.5 - Prob. 16ECh. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - Prob. 20ECh. 10.5 - Prob. 21ECh. 10.5 - Prob. 22ECh. 10.5 - Prob. 23ECh. 10.5 - Prob. 24ECh. 10.5 - Prob. 25ECh. 10.5 - Prob. 26ECh. 10.5 - Prob. 27ECh. 10.5 - Prob. 28ECh. 10.5 - Prob. 29ECh. 10.5 - Prob. 30ECh. 10.5 - Prob. 31ECh. 10.5 - Prob. 32ECh. 10.5 - Prob. 33ECh. 10.5 - Prob. 34ECh. 10.5 - Prob. 35ECh. 10.5 - Prob. 36ECh. 10.5 - Prob. 37ECh. 10.5 - Prob. 38ECh. 10.5 - Prob. 39ECh. 10.5 - Prob. 40ECh. 10.5 - Prob. 41ECh. 10.5 - Prob. 42ECh. 10.5 - Prob. 43ECh. 10.5 - Prob. 44ECh. 10.5 - Prob. 45ECh. 10.5 - Prob. 46ECh. 10.5 - Nutrition A nutritionist is studying the effects...Ch. 10.5 - Prob. 48ECh. 10.5 - Prob. 49ECh. 10.5 - Prob. 50ECh. 10.6 - True or false? det(A) is defined only for a square...Ch. 10.6 - Prob. 2ECh. 10.6 - True or false? If det(A) = 0, then A is not...Ch. 10.6 - Prob. 4ECh. 10.6 - Prob. 5ECh. 10.6 - Prob. 6ECh. 10.6 - Prob. 7ECh. 10.6 - Prob. 8ECh. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - Prob. 11ECh. 10.6 - Prob. 12ECh. 10.6 - Prob. 13ECh. 10.6 - Prob. 14ECh. 10.6 - Prob. 15ECh. 10.6 - Prob. 16ECh. 10.6 - Prob. 17ECh. 10.6 - Prob. 18ECh. 10.6 - Prob. 19ECh. 10.6 - Prob. 20ECh. 10.6 - Prob. 21ECh. 10.6 - Prob. 22ECh. 10.6 - Prob. 23ECh. 10.6 - Prob. 24ECh. 10.6 - Prob. 25ECh. 10.6 - Prob. 26ECh. 10.6 - Prob. 27ECh. 10.6 - Prob. 28ECh. 10.6 - Prob. 29ECh. 10.6 - Prob. 30ECh. 10.6 - Prob. 31ECh. 10.6 - Prob. 32ECh. 10.6 - Prob. 33ECh. 10.6 - Prob. 34ECh. 10.6 - Prob. 35ECh. 10.6 - Prob. 36ECh. 10.6 - Prob. 37ECh. 10.6 - Prob. 38ECh. 10.6 - Prob. 39ECh. 10.6 - Prob. 40ECh. 10.6 - Prob. 41ECh. 10.6 - Prob. 42ECh. 10.6 - Prob. 43ECh. 10.6 - Prob. 44ECh. 10.6 - Prob. 45ECh. 10.6 - Prob. 46ECh. 10.6 - Prob. 47ECh. 10.6 - Prob. 48ECh. 10.6 - Prob. 49ECh. 10.6 - Prob. 50ECh. 10.6 - Prob. 51ECh. 10.6 - Prob. 52ECh. 10.6 - Prob. 53ECh. 10.6 - Prob. 54ECh. 10.6 - Prob. 55ECh. 10.6 - Prob. 56ECh. 10.6 - Prob. 57ECh. 10.6 - Prob. 58ECh. 10.6 - Prob. 59ECh. 10.6 - Prob. 60ECh. 10.6 - The Arch of a Bridge The opening of a railway...Ch. 10.6 - A Triangular Plot of Land An outdoors club is...Ch. 10.6 - Prob. 63ECh. 10.6 - Prob. 64ECh. 10.6 - Prob. 65ECh. 10.6 - Prob. 66ECh. 10.6 - Prob. 67ECh. 10.7 - For each rational function r, choose from (i)(iv)...Ch. 10.7 - Prob. 2ECh. 10.7 - Prob. 3ECh. 10.7 - Prob. 4ECh. 10.7 - Prob. 5ECh. 10.7 - Prob. 6ECh. 10.7 - Prob. 7ECh. 10.7 - Prob. 8ECh. 10.7 - Prob. 9ECh. 10.7 - Prob. 10ECh. 10.7 - Prob. 11ECh. 10.7 - Prob. 12ECh. 10.7 - Prob. 13ECh. 10.7 - Prob. 14ECh. 10.7 - Prob. 15ECh. 10.7 - Prob. 16ECh. 10.7 - Prob. 17ECh. 10.7 - Prob. 18ECh. 10.7 - Prob. 19ECh. 10.7 - Prob. 20ECh. 10.7 - Prob. 21ECh. 10.7 - Prob. 22ECh. 10.7 - Prob. 23ECh. 10.7 - Prob. 24ECh. 10.7 - Prob. 25ECh. 10.7 - Prob. 26ECh. 10.7 - Prob. 27ECh. 10.7 - Prob. 28ECh. 10.7 - Prob. 29ECh. 10.7 - Prob. 30ECh. 10.7 - Prob. 31ECh. 10.7 - Prob. 32ECh. 10.7 - Prob. 33ECh. 10.7 - Prob. 34ECh. 10.7 - Prob. 35ECh. 10.7 - Prob. 36ECh. 10.7 - Prob. 37ECh. 10.7 - Prob. 38ECh. 10.7 - Prob. 39ECh. 10.7 - Prob. 40ECh. 10.7 - Prob. 41ECh. 10.7 - Prob. 42ECh. 10.7 - Prob. 43ECh. 10.7 - Prob. 44ECh. 10.7 - Prob. 45ECh. 10.7 - Prob. 46ECh. 10.7 - Prob. 47ECh. 10.7 - Prob. 48ECh. 10.8 - The system of equations {2yx2=0yx=4 is graphed...Ch. 10.8 - Prob. 2ECh. 10.8 - Prob. 3ECh. 10.8 - Prob. 4ECh. 10.8 - Prob. 5ECh. 10.8 - Prob. 6ECh. 10.8 - Prob. 7ECh. 10.8 - Prob. 8ECh. 10.8 - Prob. 9ECh. 10.8 - Prob. 10ECh. 10.8 - Prob. 11ECh. 10.8 - Prob. 12ECh. 10.8 - Prob. 13ECh. 10.8 - Prob. 14ECh. 10.8 - Prob. 15ECh. 10.8 - Prob. 16ECh. 10.8 - Prob. 17ECh. 10.8 - Prob. 18ECh. 10.8 - Prob. 19ECh. 10.8 - Prob. 20ECh. 10.8 - Prob. 21ECh. 10.8 - Prob. 22ECh. 10.8 - Prob. 23ECh. 10.8 - Prob. 24ECh. 10.8 - Prob. 25ECh. 10.8 - Prob. 26ECh. 10.8 - Prob. 27ECh. 10.8 - Prob. 28ECh. 10.8 - Prob. 29ECh. 10.8 - Prob. 30ECh. 10.8 - Prob. 31ECh. 10.8 - Prob. 32ECh. 10.8 - Prob. 33ECh. 10.8 - Prob. 34ECh. 10.8 - Prob. 35ECh. 10.8 - Prob. 36ECh. 10.8 - Prob. 37ECh. 10.8 - Prob. 38ECh. 10.8 - Prob. 39ECh. 10.8 - Prob. 40ECh. 10.8 - Dimensions of a Rectangle A rectangle has an area...Ch. 10.8 - Legs of a Right Triangle A right triangle has an...Ch. 10.8 - Dimensions of a Rectangle The perimeter of a...Ch. 10.8 - Dimensions of a Rectangle A circular piece of...Ch. 10.8 - Flight of a Rocket A hill is inclined so that its...Ch. 10.8 - Making a Stovepipe A rectangular piece of sheet...Ch. 10.8 - Global Positioning System (GPS) The Global...Ch. 10.8 - Prob. 48ECh. 10.8 - Prob. 49ECh. 10.9 - To graph an inequality, we first graph the...Ch. 10.9 - Prob. 2ECh. 10.9 - Prob. 3ECh. 10.9 - Prob. 4ECh. 10.9 - Prob. 5ECh. 10.9 - Prob. 6ECh. 10.9 - Prob. 7ECh. 10.9 - Prob. 8ECh. 10.9 - Prob. 9ECh. 10.9 - Prob. 10ECh. 10.9 - Prob. 11ECh. 10.9 - Prob. 12ECh. 10.9 - Prob. 13ECh. 10.9 - Prob. 14ECh. 10.9 - Prob. 15ECh. 10.9 - Prob. 16ECh. 10.9 - Prob. 17ECh. 10.9 - Prob. 18ECh. 10.9 - Prob. 19ECh. 10.9 - Prob. 20ECh. 10.9 - Prob. 21ECh. 10.9 - Prob. 22ECh. 10.9 - Prob. 23ECh. 10.9 - Prob. 24ECh. 10.9 - Prob. 25ECh. 10.9 - Prob. 26ECh. 10.9 - Prob. 27ECh. 10.9 - Prob. 28ECh. 10.9 - Prob. 29ECh. 10.9 - Prob. 30ECh. 10.9 - Prob. 31ECh. 10.9 - Prob. 32ECh. 10.9 - Prob. 33ECh. 10.9 - Prob. 34ECh. 10.9 - Prob. 35ECh. 10.9 - Prob. 36ECh. 10.9 - Prob. 37ECh. 10.9 - Prob. 38ECh. 10.9 - Prob. 39ECh. 10.9 - Prob. 40ECh. 10.9 - Prob. 41ECh. 10.9 - Prob. 42ECh. 10.9 - Prob. 43ECh. 10.9 - Prob. 44ECh. 10.9 - Prob. 45ECh. 10.9 - Prob. 46ECh. 10.9 - Prob. 47ECh. 10.9 - Prob. 48ECh. 10.9 - Prob. 49ECh. 10.9 - Prob. 50ECh. 10.9 - Prob. 51ECh. 10.9 - Prob. 52ECh. 10.9 - Coffee Blends A coffee merchant sells two...Ch. 10.9 - Nutrition A cat food manufacturer uses fish and...Ch. 10.9 - Prob. 55ECh. 10 - Prob. 1RCCCh. 10 - Prob. 2RCCCh. 10 - Prob. 3RCCCh. 10 - Prob. 4RCCCh. 10 - Prob. 5RCCCh. 10 - Prob. 6RCCCh. 10 - Prob. 7RCCCh. 10 - Prob. 8RCCCh. 10 - Prob. 9RCCCh. 10 - Prob. 10RCCCh. 10 - Prob. 11RCCCh. 10 - Prob. 12RCCCh. 10 - Prob. 13RCCCh. 10 - Prob. 14RCCCh. 10 - Prob. 15RCCCh. 10 - Prob. 16RCCCh. 10 - Prob. 17RCCCh. 10 - Prob. 18RCCCh. 10 - Prob. 19RCCCh. 10 - Prob. 1RECh. 10 - Prob. 2RECh. 10 - Prob. 3RECh. 10 - Prob. 4RECh. 10 - Prob. 5RECh. 10 - Prob. 6RECh. 10 - Prob. 7RECh. 10 - Prob. 8RECh. 10 - Prob. 9RECh. 10 - Prob. 10RECh. 10 - Prob. 11RECh. 10 - Prob. 12RECh. 10 - Prob. 13RECh. 10 - Prob. 14RECh. 10 - Prob. 15RECh. 10 - Prob. 16RECh. 10 - Prob. 17RECh. 10 - Prob. 18RECh. 10 - Prob. 19RECh. 10 - Prob. 20RECh. 10 - Prob. 21RECh. 10 - Prob. 22RECh. 10 - Prob. 23RECh. 10 - Prob. 24RECh. 10 - Prob. 25RECh. 10 - Prob. 26RECh. 10 - Prob. 27RECh. 10 - Prob. 28RECh. 10 - Prob. 29RECh. 10 - Prob. 30RECh. 10 - Prob. 31RECh. 10 - Prob. 32RECh. 10 - Prob. 33RECh. 10 - Prob. 34RECh. 10 - Prob. 35RECh. 10 - Prob. 36RECh. 10 - Prob. 37RECh. 10 - Prob. 38RECh. 10 - Prob. 39RECh. 10 - Prob. 40RECh. 10 - Prob. 41RECh. 10 - Prob. 42RECh. 10 - Prob. 43RECh. 10 - Prob. 44RECh. 10 - Prob. 45RECh. 10 - Prob. 46RECh. 10 - Prob. 47RECh. 10 - Prob. 48RECh. 10 - Prob. 49RECh. 10 - Prob. 50RECh. 10 - Prob. 51RECh. 10 - Prob. 52RECh. 10 - Prob. 53RECh. 10 - Prob. 54RECh. 10 - Prob. 55RECh. 10 - Prob. 56RECh. 10 - Prob. 57RECh. 10 - Prob. 58RECh. 10 - Prob. 59RECh. 10 - Prob. 60RECh. 10 - Prob. 61RECh. 10 - Prob. 62RECh. 10 - Prob. 63RECh. 10 - Prob. 64RECh. 10 - Prob. 65RECh. 10 - Prob. 66RECh. 10 - Prob. 67RECh. 10 - Prob. 68RECh. 10 - Prob. 69RECh. 10 - Prob. 70RECh. 10 - Prob. 71RECh. 10 - Prob. 72RECh. 10 - Prob. 73RECh. 10 - Prob. 74RECh. 10 - Prob. 75RECh. 10 - Prob. 76RECh. 10 - Prob. 77RECh. 10 - Prob. 78RECh. 10 - Prob. 79RECh. 10 - Prob. 80RECh. 10 - Prob. 81RECh. 10 - Prob. 82RECh. 10 - Prob. 83RECh. 10 - Prob. 84RECh. 10 - Prob. 85RECh. 10 - Prob. 86RECh. 10 - Prob. 87RECh. 10 - Prob. 88RECh. 10 - Prob. 89RECh. 10 - Prob. 90RECh. 10 - Prob. 91RECh. 10 - Prob. 92RECh. 10 - Prob. 93RECh. 10 - Prob. 94RECh. 10 - Prob. 95RECh. 10 - Prob. 96RECh. 10 - Prob. 97RECh. 10 - Prob. 98RECh. 10 - Prob. 99RECh. 10 - Prob. 100RECh. 10 - Prob. 101RECh. 10 - Prob. 102RECh. 10 - Prob. 103RECh. 10 - Prob. 104RECh. 10 - Prob. 105RECh. 10 - Prob. 106RECh. 10 - Prob. 107RECh. 10 - Prob. 108RECh. 10 - Prob. 109RECh. 10 - Prob. 110RECh. 10 - Prob. 111RECh. 10 - Prob. 112RECh. 10 - Prob. 1TCh. 10 - Prob. 2TCh. 10 - Prob. 3TCh. 10 - Prob. 4TCh. 10 - Prob. 5TCh. 10 - Prob. 6TCh. 10 - Prob. 7TCh. 10 - Anne, Barry, and Cathy enter a coffee shop. Anne...Ch. 10 - Prob. 9TCh. 10 - Prob. 10TCh. 10 - Only one of the following matrices has an inverse....Ch. 10 - Prob. 12TCh. 10 - Prob. 13TCh. 10 - Prob. 14TCh. 10 - Find the maximum and minimum values of the given...Ch. 10 - Prob. 2PCh. 10 - Prob. 3PCh. 10 - Find the maximum and minimum value of the given...Ch. 10 - Making Furniture A furniture manufacturer makes...Ch. 10 - A Housing Development A housing contractor has...Ch. 10 - Hauling Fruit A trucker hauls citrus fruit from...Ch. 10 - Manufacturing Calculators A manufacturer of...Ch. 10 - Shipping Televisions An electronics discount chain...Ch. 10 - Prob. 10PCh. 10 - Packaging Nuts A confectioner sells two types of...Ch. 10 - Feeding Lab Rabbits A biologist wishes to feed...Ch. 10 - Investing in Bonds A woman wishes to invest 12,000...Ch. 10 - Prob. 14PCh. 10 - Business Strategy A small software company...Ch. 10 - Feasible Region All parts of this problem refer to...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- A New Heating System A homeowner wants to replace their old heating system. Energy is measured in kilowatt-hours (kWh). It takes about 11,700 kWh of energy to heat the house for the winter. The current heating system uses natural gas and is 60% efficient, which means that for every 100 kWh of natural gas it uses, it produces 60 kWh of heat. With the homeowner's current system, it costs $975 to heat the house. Assume that natural gas costs $0.05/kWh and electricity costs $0.21/kWh. The homeowner also has an air conditioner that uses 2,500 kWh of electricity per year and produces 290 kWh of cooling for every 100 kWh it uses. They also have a water heater that uses 4,300 kWh of electricity per year and produces 90 kWh of heat for every 100 kWh it uses. These systems could also be replaced if there is a cheaper option, but it isn't necessary. Here are three other types of heating systems the homeowner could replace their current system with: • A new furnace which also runs on natural gas…arrow_forwardFind a unit normal vector to the surface f(x, y, z) = 0 at the point P(-3,4, -32) for the function f(x, y, z) = In -4x -5y- Please write your answer as a vector (a, b, c) with a negative z component, and show your answer accurate to 4 decimal placesarrow_forwardFind the differential of the function f(x, y) = 2x² - 2xy – 5y² at the point (-6, -5) using Ax = 0.3 and Ay = 0.05. dz = Now find Az and compare it to your answer above Ax= Hint: If entering a decimal, round to at least 5 placesarrow_forward
- Find the differential of the function f(x, y) = −8x√y at the point (1,3) using Ax = 0.25 and Ay = -0.15. dz Now find Az and compare it to your answer above Az = Hint: If entering a decimal, round to at least 5 placesarrow_forwardplease dont use chat gpt i need to underarrow_forwardChris Lynch plans to invest $200 into a money market account. Find the interest rate that is needed for the money to grow to $1,800 in 12 years if the interest is compounded quarterly. The rate is %. (Round to the nearest percent.)arrow_forward
- Find the interest earned on $10,000 invested for 6 years at 6% interest compounded as follows. a. Annually b. Semiannually (twice a year) c. Quarterly d. Monthly e. Continuouslyarrow_forward6.9x y= 100-x a. Find the cost of removing each percent of pollutants: 50%; 70%; 80%; 90%; 95%; 98%; 99%. 50% y = 70% y = 80% y = 90% YF 95% y = 98% y= 99% V =arrow_forwardThe cost per ton, y, to build an oil tanker of x thousand deadweight tons was approximated by 215,000 C(x)= x+485 C(25) C(100) C(300) =1 C(50) = = C(200) = C(400) =arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
UG/ linear equation in linear algebra; Author: The Gate Academy;https://www.youtube.com/watch?v=aN5ezoOXX5A;License: Standard YouTube License, CC-BY
System of Linear Equations-I; Author: IIT Roorkee July 2018;https://www.youtube.com/watch?v=HOXWRNuH3BE;License: Standard YouTube License, CC-BY