
Manufacturing Calculators A manufacturer of calculators produces two models: standard and scientific. Long-term demand for the two models mandates that the company manufacture at least 100 standard and 80 scientific calculators each day. However, because of limitations on production capacity, no more than 200 standard and 170 scientific calculators can be made daily. To satisfy a shipping contract, a total of at least 200 calculators must be shipped every day.
- (a) If the production cost is $5 for a standard calculator and $7 for a scientific one, how many of each model should be produced daily to minimize this cost?
- (b) If each standard calculator results in a $2 loss but each scientific one produces a $5 profit, how many of each model should be made daily to maximize profit?
(a)
To find: The number of standard and scientific calculators produced daily to minimize the cost.
Answer to Problem 8P
The company makes the 120 standard and 80 scientific calculators to minimize the production cost.
Explanation of Solution
Given:
The company manufactures at least 100 standard and 80 scientific calculators each day.
Due to limitation on production capacity, no more than 200 standard and 170 scientific calculators made daily.
The production cost on standard calculators is
Calculation:
Let the number of daily production of the standard calculators is x and the number of daily production of the scientific calculators is y.
Use the given information to make the inequalities and the objective function for the feasible region.
The required information is shown in the table below.
| Standard calculators(x) |
Scientific Calculators(y) | |
| At-least production | 100 | 80 |
| Not more than production | 200 | 170 |
| Profit |
|
|
The Production function is,
The constraint to get the feasible region has shown below.
The production of at least 100 standard and 80 scientific calculators each day represented as,
And,
The production limit of the calculators is represented as,
And,
The total number of calculators must be shipped from the company at least 200.
Now, take the equalities of the above inequalities,
And,
Substitute 100 for x in the equation (1).
Thus, the intersection point is
Substitute
The intersection point is
Substitute 170 for y in equation (2),
Substitute
The intersection point is
Now, draw the graph of the above equations,
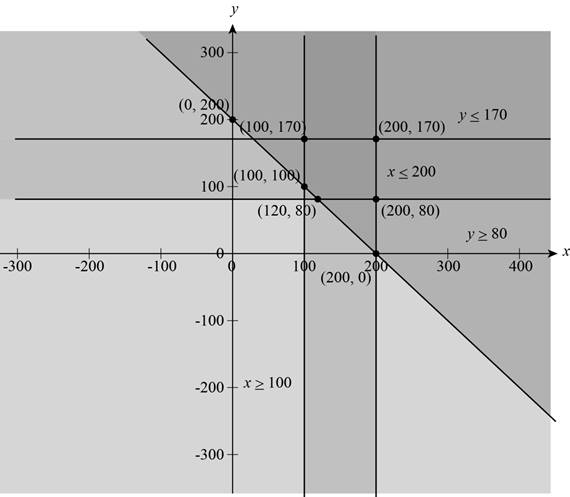
Figure (1)
The vertices which lies in the feasible region is shown below,
Substitute the 100 for x and 170 for y in the Production function
Substitute the 100 for x and 100 for y in the objective function
Substitute the 120 for x and 8 for y in the objective function
Substitute the 200 for x and 80 for y in the objective function
Substitute the 200 for x and 170 for y in the objective function
So, all the satisfies these vertices are shown in the table below.
| Vertices |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Thus, the minimum production cost is
(b)
To find: The number of standard and scientific calculators produced daily to maximize the profit if the standard calculators produces loss of
Answer to Problem 8P
The company makes the 100 standard and 170 scientific calculators to maximize the profit.
Explanation of Solution
Given:
The company manufactures at least 100 standard and 80 scientific calculators each day.
Due to limitation on production capacity, no more than 200 standard and 170 scientific calculators made daily.
The each standard calculator produces a loss of
Calculation:
Let the number of daily production of the standard calculators is x and the number of daily production of the scientific calculators is y.
Use the given information to make the inequalities and the objective function for the feasible region.
The required information is shown in the table below.
| Standard calculators(x) |
Scientific Calculators(y) | |
| At-least production | 100 | 80 |
| Not more than production | 200 | 170 |
| Profit |
|
|
The Production function is,
From the figure (1) of the part (a) keep similar constraints are shown below.
And,
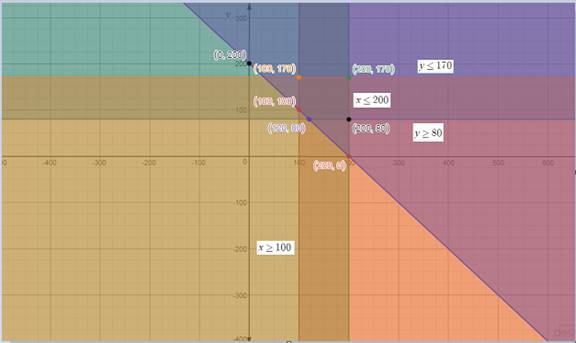
Figure (1)
The vertices which lies in the feasible region is shown below.
Substitute the 100 for x and 170 for y in the Production function
Substitute the 100 for x and 100 for y in the objective function
Substitute the 120 for x and 8 for y in the objective function
Substitute the 200 for x and 80 for y in the objective function
Substitute the 200 for x and 170 for y in the objective function
So, all the satisfies these vertices are shown in the table below.
| Vertices |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Thus, the maximum production cost is
Chapter 10 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
- Ministry of Higher Education & Scientific Research Babylon University College of Engineering - Al musayab Automobile Department Subject :Engineering Analysis Time: 2 hour Date:27-11-2022 کورس اول تحليلات تعمیر ) 1st month exam / 1st semester (2022-2023)/11/27 Note: Answer all questions,all questions have same degree. Q1/: Find the following for three only. 1- 4s C-1 (+2-3)2 (219) 3.0 (6+1)) (+3+5) (82+28-3),2- ,3- 2-1 4- Q2/:Determine the Laplace transform of the function t sint. Q3/: Find the Laplace transform of 1, 0≤t<2, -2t+1, 2≤t<3, f(t) = 3t, t-1, 3≤t 5, t≥ 5 Q4: Find the Fourier series corresponding to the function 0 -5arrow_forwardMinistry of Higher Education & Scientific Research Babylon University College of Engineering - Al musayab Subject :Engineering Analysis Time: 80 min Date:11-12-2022 Automobile Department 2nd month exam / 1" semester (2022-2023) Note: Answer all questions,all questions have same degree. کورس اول شعر 3 Q1/: Use a Power series to solve the differential equation: y" - xy = 0 Q2/:Evaluate using Cauchy's residue theorem, sinnz²+cosz² dz, where C is z = 3 (z-1)(z-2) Q3/:Evaluate dz (z²+4)2 Where C is the circle /z-i/-2,using Cauchy's residue theorem. Examiner: Dr. Wisam N. Hassanarrow_forwardMinistry of Higher Education & Scientific Research Babylon University College of Engineering - Al musayab Subject :Engineering Analysis Time: 80 min Date:11-12-2022 Automobile Department 2nd month exam / 1" semester (2022-2023) Note: Answer all questions,all questions have same degree. کورس اول شعر 3 Q1/: Use a Power series to solve the differential equation: y" - xy = 0 Q2/:Evaluate using Cauchy's residue theorem, sinnz²+cosz² dz, where C is z = 3 (z-1)(z-2) Q3/:Evaluate dz (z²+4)2 Where C is the circle /z-i/-2,using Cauchy's residue theorem. Examiner: Dr. Wisam N. Hassanarrow_forwardWhich degenerate conic is formed when a double cone is sliced through the apex by a plane parallel to the slant edge of the cone?arrow_forward1/ Solve the following: 1 x + X + cos(3X) -75 -1 2 2 (5+1) e 5² + 5 + 1 3 L -1 1 5² (5²+1) 1 5(5-5)arrow_forwardI need expert handwritten solution.to this integralarrow_forwardExample: If ƒ (x + 2π) = ƒ (x), find the Fourier expansion f(x) = eax in the interval [−π,π]arrow_forwardExample: If ƒ (x + 2π) = ƒ (x), find the Fourier expansion f(x) = eax in the interval [−π,π]arrow_forwardPlease can you give detailed steps on how the solutions change from complex form to real form. Thanks.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





