Precalculus: Mathematics for Calculus - 6th Edition
Precalculus: Mathematics for Calculus - 6th Edition
6th Edition
ISBN: 9780840068071
Author: Stewart, James, Redlin, Lothar, Watson, Saleem
Publisher: Cengage Learning
bartleby

Videos

Textbook Question
Book Icon
Chapter 10, Problem 15P

Business Strategy A small software company publishes computer games, educational software, and utility software. Their business strategy is to market a total of 36 new programs each year, at least four of these being games. The number of utility programs published is never more than twice the number of educational programs. On average, the company makes an annual profit of $5000 on each computer game, $8000 on each educational program, and $6000 on each utility program. How many of each type of software should the company publish annually for maximum profit?

Expert Solution & Answer
Check Mark
To determine

To find: The number of computer games, educational program and utility program should the company publish annually for maximum profit.

Answer to Problem 15P

The company publishes the 4 four computer games, 32 educational software and 0 utility programs to get the maximum profit.

Explanation of Solution

Given:

The business strategy of the company to launch the 36 new programs each year and at least four of being games.

The number of utility programs published is not more than twice the number of educational programs.

The company annual profit on each computer games is $5000 , on each educational program is $8000 and on each utility program is $6000 .

Calculation:

Let the number of computer games published in a year is x and number of educational videos published in a year is y.

Then the number of utility program is (36−x−y) .

Use the given information to make the inequalities and the objective function for the feasible region.

The required information is shown in the table below.

Computer games Educational programs Utility programs
Number of games x y (36−x−y)
Profit $5000 $8000 $6000

The objective function is,

I=5000x+8000y+6000(36−x−y)=5000x+8000y+216000−6000x−6000y=216000−1000x+2000y ,

The constraint to get the feasible region has shown below.

The company makes at least 4 computer games.

x≥4

The number of utility programs published is not more than twice the number of educational programs.

2y≥36−x−yx+3y≥36

And,

36−x−y≥0x+y≤36

And,

x≥0,y≥0

Now, take the equalities of the above inequalities,

x=4 , x=0,y=0

And,

x+3y=36 (1)

And,

x+y=36 (2)

Substitute 4 for x in the equation (1).

4+3y=363y=36−43y=32y=323

The intersection point is (x,y)=(4,323) .

Substitute 4 for x in the equation (2).

4+y=36y=36−4y=32

The intersection point is (x,y)=(4,32) .

Now, get the value of y in terms of x from the equation (3) to find the intersection points of equation (1) and (2),

x+y=36y=36−x (3)

Substitute 36−x for y in equation (1),

x+3y=36x+3(36−x)=36x+108−3x=362x=72

Further solve the above equation,

x=36

Substitute 36 for x in equation (3),

y=36−36=0

The intersection point is (x,y)=(36,0) .

Now, draw the graph of the above equations,

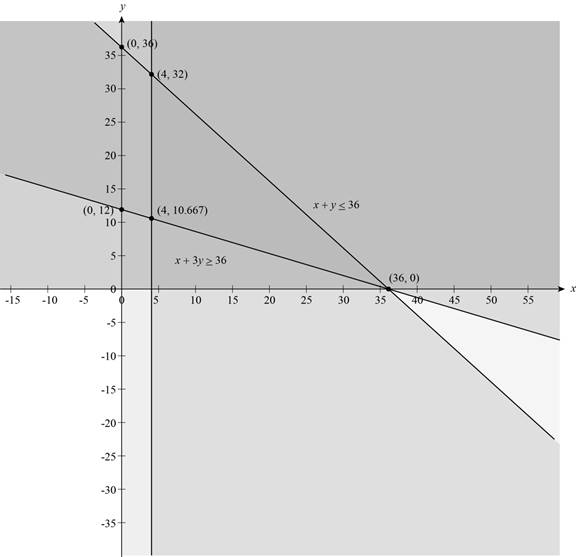
Precalculus: Mathematics for Calculus - 6th Edition, Chapter 10, Problem 15P

Figure (1)

The vertices which lies in the feasible region is shown below.

(36,0),(4,323),(4,32)

Substitute the 36 for x and 0 for y in the objective function I=216000−1000x+2000y ,

I=216000−1000x+2000y=216000−1000⋅36+2000⋅0=216000−36000=180000

Substitute the 4 for x and 32 for y in the objective function I=216000−1000x+2000y ,

I=216000−1000x+2000y=216000−1000⋅4+2000⋅32=216000−4000+64000=276000

Substitute the 4 for x and 323 for y in the objective function I=216000−1000x+2000y ,

I=216000−1000x+2000y=216000−1000⋅4+2000⋅323=216000−4000+640003=212000+21333.33

Further solve the above equation,

I=233333.33

So, point satisfies these vertices are shown in the table below.

Vertices I=216000−1000x+2000y
(36,0) 180000
(4,323) 233333.33
(4,32) 276000(Maximum)

The maximum interest rate is 276000 with the 4 computer program, 32 educational programs. Then the utility programs is,

36−x−y=36−4−32=0

Thus, a company made 4 computer programs, 32 educational programs and 0 utility programs at maximum interest for the objective function I=216000−1000x+2000y .

Previous
Chapter 10, Problem 14P
Next
Chapter 10, Problem 16P

Chapter 10 Solutions

Precalculus: Mathematics for Calculus - 6th Edition

Ch. 10.1 - The system of equations {2x+3y=75xy=9 is a system...Ch. 10.1 - Prob. 2ECh. 10.1 - A system of two linear equations in two variables...Ch. 10.1 - The following is a system of two linear equations...Ch. 10.1 - Prob. 5ECh. 10.1 - Prob. 6ECh. 10.1 - Prob. 7ECh. 10.1 - Prob. 8ECh. 10.1 - Prob. 9ECh. 10.1 - Prob. 10E
Ch. 10.1 - Prob. 11ECh. 10.1 - Prob. 12ECh. 10.1 - Prob. 13ECh. 10.1 - Prob. 14ECh. 10.1 - Prob. 15ECh. 10.1 - Prob. 16ECh. 10.1 - Prob. 17ECh. 10.1 - Prob. 18ECh. 10.1 - Prob. 19ECh. 10.1 - Prob. 20ECh. 10.1 - Prob. 21ECh. 10.1 - Prob. 22ECh. 10.1 - Prob. 23ECh. 10.1 - Prob. 24ECh. 10.1 - Prob. 25ECh. 10.1 - Prob. 26ECh. 10.1 - Prob. 27ECh. 10.1 - Prob. 28ECh. 10.1 - Prob. 29ECh. 10.1 - Prob. 30ECh. 10.1 - Prob. 31ECh. 10.1 - Prob. 32ECh. 10.1 - Prob. 33ECh. 10.1 - Prob. 34ECh. 10.1 - Prob. 35ECh. 10.1 - Prob. 36ECh. 10.1 - Prob. 37ECh. 10.1 - Prob. 38ECh. 10.1 - Prob. 39ECh. 10.1 - Prob. 40ECh. 10.1 - Prob. 41ECh. 10.1 - Prob. 42ECh. 10.1 - Prob. 43ECh. 10.1 - Prob. 44ECh. 10.1 - Prob. 45ECh. 10.1 - Prob. 46ECh. 10.1 - Prob. 47ECh. 10.1 - Prob. 48ECh. 10.1 - Prob. 49ECh. 10.1 - Prob. 50ECh. 10.1 - Prob. 51ECh. 10.1 - Prob. 52ECh. 10.1 - Prob. 53ECh. 10.1 - Prob. 54ECh. 10.1 - Prob. 55ECh. 10.1 - Prob. 56ECh. 10.1 - Prob. 57ECh. 10.1 - Prob. 58ECh. 10.1 - Value of Coins A man has 14 coins in his pocket,...Ch. 10.1 - Admission Fees The admission fee at an amusement...Ch. 10.1 - Gas Station A gas station sells regular gas for...Ch. 10.1 - Fruit Stand A fruit stand sells two varieties of...Ch. 10.1 - Airplane Speed A man flies a small airplane from...Ch. 10.1 - Boat Speed A boat on a river travels downstream...Ch. 10.1 - Nutrition A researcher performs an experiment to...Ch. 10.1 - Coffee Blends A customer in a coffee shop...Ch. 10.1 - Mixture Problem A chemist has two large containers...Ch. 10.1 - Mixture Problem A biologist has two brine...Ch. 10.1 - Investments A woman invests a total of 20,000 in...Ch. 10.1 - Investments A man invests his savings in two...Ch. 10.1 - Prob. 71ECh. 10.1 - Prob. 72ECh. 10.1 - Prob. 73ECh. 10.1 - Area of a Triangle Find the area of the triangle...Ch. 10.1 - Prob. 75ECh. 10.2 - These exercises refer to the following system:...Ch. 10.2 - Prob. 2ECh. 10.2 - Prob. 3ECh. 10.2 - Prob. 4ECh. 10.2 - Prob. 5ECh. 10.2 - Prob. 6ECh. 10.2 - Prob. 7ECh. 10.2 - Prob. 8ECh. 10.2 - Prob. 9ECh. 10.2 - Prob. 10ECh. 10.2 - Prob. 11ECh. 10.2 - Prob. 12ECh. 10.2 - Prob. 13ECh. 10.2 - Prob. 14ECh. 10.2 - Prob. 15ECh. 10.2 - Prob. 16ECh. 10.2 - Prob. 17ECh. 10.2 - Prob. 18ECh. 10.2 - Prob. 19ECh. 10.2 - Prob. 20ECh. 10.2 - Prob. 21ECh. 10.2 - Prob. 22ECh. 10.2 - Prob. 23ECh. 10.2 - Prob. 24ECh. 10.2 - Prob. 25ECh. 10.2 - Prob. 26ECh. 10.2 - Prob. 27ECh. 10.2 - Prob. 28ECh. 10.2 - Prob. 29ECh. 10.2 - Prob. 30ECh. 10.2 - Prob. 31ECh. 10.2 - Prob. 32ECh. 10.2 - Prob. 33ECh. 10.2 - Prob. 34ECh. 10.2 - Prob. 35ECh. 10.2 - Prob. 36ECh. 10.2 - Prob. 37ECh. 10.2 - Prob. 38ECh. 10.2 - Prob. 39ECh. 10.2 - Gas Station A gas station sells three types of...Ch. 10.2 - Nutrition A biologist is performing an experiment...Ch. 10.2 - Diet Program Nicole started a new diet that...Ch. 10.2 - Juice Blends The Juice Company offers three kinds...Ch. 10.2 - Appliance Manufacturing Kitchen Korner produces...Ch. 10.2 - Stock Portfolio An investor owns three stocks: A,...Ch. 10.2 - Electricity By using Kirchhoffs Laws, it can be...Ch. 10.2 - Prob. 47ECh. 10.3 - If a system of linear equations has infinitely...Ch. 10.3 - Prob. 2ECh. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Prob. 7ECh. 10.3 - Prob. 8ECh. 10.3 - Prob. 9ECh. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Prob. 12ECh. 10.3 - Prob. 13ECh. 10.3 - Prob. 14ECh. 10.3 - Prob. 15ECh. 10.3 - Prob. 16ECh. 10.3 - Prob. 17ECh. 10.3 - Prob. 18ECh. 10.3 - Prob. 19ECh. 10.3 - Prob. 20ECh. 10.3 - Prob. 21ECh. 10.3 - Prob. 22ECh. 10.3 - Prob. 23ECh. 10.3 - Prob. 24ECh. 10.3 - Prob. 25ECh. 10.3 - Prob. 26ECh. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Prob. 29ECh. 10.3 - Prob. 30ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 32ECh. 10.3 - Prob. 33ECh. 10.3 - Prob. 34ECh. 10.3 - Prob. 35ECh. 10.3 - Prob. 36ECh. 10.3 - Prob. 37ECh. 10.3 - Prob. 38ECh. 10.3 - Prob. 39ECh. 10.3 - Prob. 40ECh. 10.3 - Prob. 41ECh. 10.3 - Prob. 42ECh. 10.3 - Prob. 43ECh. 10.3 - Prob. 44ECh. 10.3 - Prob. 45ECh. 10.3 - Prob. 46ECh. 10.3 - Prob. 47ECh. 10.3 - Prob. 48ECh. 10.3 - Prob. 49ECh. 10.3 - Prob. 50ECh. 10.3 - Prob. 51ECh. 10.3 - Prob. 52ECh. 10.3 - Prob. 53ECh. 10.3 - Prob. 54ECh. 10.3 - Nutrition A doctor recommends that a patient take...Ch. 10.3 - Mixtures A chemist has three acid solutions at...Ch. 10.3 - Distance, Speed, and Time Amanda, Bryce, and Corey...Ch. 10.3 - Classroom Use A small school has 100 students who...Ch. 10.3 - Manufacturing Furniture A furniture factory makes...Ch. 10.3 - Traffic Flow A section of a citys street network...Ch. 10.3 - Prob. 61ECh. 10.4 - We can add (or subtract) two matrices only if they...Ch. 10.4 - (a) We can multiply two matrices only if the...Ch. 10.4 - Prob. 3ECh. 10.4 - Fill in the missing entries in the product matrix....Ch. 10.4 - Prob. 5ECh. 10.4 - Prob. 6ECh. 10.4 - Prob. 7ECh. 10.4 - Prob. 8ECh. 10.4 - Prob. 9ECh. 10.4 - Prob. 10ECh. 10.4 - Prob. 11ECh. 10.4 - Prob. 12ECh. 10.4 - Prob. 13ECh. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Prob. 17ECh. 10.4 - Prob. 18ECh. 10.4 - Prob. 19ECh. 10.4 - Prob. 20ECh. 10.4 - Prob. 21ECh. 10.4 - Prob. 22ECh. 10.4 - Prob. 23ECh. 10.4 - Prob. 24ECh. 10.4 - Prob. 25ECh. 10.4 - Prob. 26ECh. 10.4 - Prob. 27ECh. 10.4 - Prob. 28ECh. 10.4 - Prob. 29ECh. 10.4 - Prob. 30ECh. 10.4 - Prob. 31ECh. 10.4 - Prob. 32ECh. 10.4 - Prob. 33ECh. 10.4 - Prob. 34ECh. 10.4 - Prob. 35ECh. 10.4 - Prob. 36ECh. 10.4 - Prob. 37ECh. 10.4 - Prob. 38ECh. 10.4 - Prob. 39ECh. 10.4 - Prob. 40ECh. 10.4 - Prob. 41ECh. 10.4 - Prob. 42ECh. 10.4 - Prob. 43ECh. 10.4 - Prob. 44ECh. 10.4 - Fast-Food Sales A small fast-food chain with...Ch. 10.4 - Prob. 46ECh. 10.4 - Canning Tomato Products Jaeger Foods produces...Ch. 10.4 - Produce Sales A farmers three children, Amy, Beth,...Ch. 10.4 - Digital Images A four-level gray scale is shown...Ch. 10.4 - Prob. 50ECh. 10.4 - Prob. 51ECh. 10.4 - Prob. 52ECh. 10.4 - Prob. 53ECh. 10.5 - (a) The matrix I=[1001] is called an __________...Ch. 10.5 - Prob. 2ECh. 10.5 - Prob. 3ECh. 10.5 - Prob. 4ECh. 10.5 - Prob. 5ECh. 10.5 - Prob. 6ECh. 10.5 - Prob. 7ECh. 10.5 - Prob. 8ECh. 10.5 - Prob. 9ECh. 10.5 - Prob. 10ECh. 10.5 - Prob. 11ECh. 10.5 - Prob. 12ECh. 10.5 - Prob. 13ECh. 10.5 - Prob. 14ECh. 10.5 - Prob. 15ECh. 10.5 - Prob. 16ECh. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - Prob. 20ECh. 10.5 - Prob. 21ECh. 10.5 - Prob. 22ECh. 10.5 - Prob. 23ECh. 10.5 - Prob. 24ECh. 10.5 - Prob. 25ECh. 10.5 - Prob. 26ECh. 10.5 - Prob. 27ECh. 10.5 - Prob. 28ECh. 10.5 - Prob. 29ECh. 10.5 - Prob. 30ECh. 10.5 - Prob. 31ECh. 10.5 - Prob. 32ECh. 10.5 - Prob. 33ECh. 10.5 - Prob. 34ECh. 10.5 - Prob. 35ECh. 10.5 - Prob. 36ECh. 10.5 - Prob. 37ECh. 10.5 - Prob. 38ECh. 10.5 - Prob. 39ECh. 10.5 - Prob. 40ECh. 10.5 - Prob. 41ECh. 10.5 - Prob. 42ECh. 10.5 - Prob. 43ECh. 10.5 - Prob. 44ECh. 10.5 - Prob. 45ECh. 10.5 - Prob. 46ECh. 10.5 - Nutrition A nutritionist is studying the effects...Ch. 10.5 - Prob. 48ECh. 10.5 - Prob. 49ECh. 10.5 - Prob. 50ECh. 10.6 - True or false? det(A) is defined only for a square...Ch. 10.6 - Prob. 2ECh. 10.6 - True or false? If det(A) = 0, then A is not...Ch. 10.6 - Prob. 4ECh. 10.6 - Prob. 5ECh. 10.6 - Prob. 6ECh. 10.6 - Prob. 7ECh. 10.6 - Prob. 8ECh. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - Prob. 11ECh. 10.6 - Prob. 12ECh. 10.6 - Prob. 13ECh. 10.6 - Prob. 14ECh. 10.6 - Prob. 15ECh. 10.6 - Prob. 16ECh. 10.6 - Prob. 17ECh. 10.6 - Prob. 18ECh. 10.6 - Prob. 19ECh. 10.6 - Prob. 20ECh. 10.6 - Prob. 21ECh. 10.6 - Prob. 22ECh. 10.6 - Prob. 23ECh. 10.6 - Prob. 24ECh. 10.6 - Prob. 25ECh. 10.6 - Prob. 26ECh. 10.6 - Prob. 27ECh. 10.6 - Prob. 28ECh. 10.6 - Prob. 29ECh. 10.6 - Prob. 30ECh. 10.6 - Prob. 31ECh. 10.6 - Prob. 32ECh. 10.6 - Prob. 33ECh. 10.6 - Prob. 34ECh. 10.6 - Prob. 35ECh. 10.6 - Prob. 36ECh. 10.6 - Prob. 37ECh. 10.6 - Prob. 38ECh. 10.6 - Prob. 39ECh. 10.6 - Prob. 40ECh. 10.6 - Prob. 41ECh. 10.6 - Prob. 42ECh. 10.6 - Prob. 43ECh. 10.6 - Prob. 44ECh. 10.6 - Prob. 45ECh. 10.6 - Prob. 46ECh. 10.6 - Prob. 47ECh. 10.6 - Prob. 48ECh. 10.6 - Prob. 49ECh. 10.6 - Prob. 50ECh. 10.6 - Prob. 51ECh. 10.6 - Prob. 52ECh. 10.6 - Prob. 53ECh. 10.6 - Prob. 54ECh. 10.6 - Prob. 55ECh. 10.6 - Prob. 56ECh. 10.6 - Prob. 57ECh. 10.6 - Prob. 58ECh. 10.6 - Prob. 59ECh. 10.6 - Prob. 60ECh. 10.6 - The Arch of a Bridge The opening of a railway...Ch. 10.6 - A Triangular Plot of Land An outdoors club is...Ch. 10.6 - Prob. 63ECh. 10.6 - Prob. 64ECh. 10.6 - Prob. 65ECh. 10.6 - Prob. 66ECh. 10.6 - Prob. 67ECh. 10.7 - For each rational function r, choose from (i)(iv)...Ch. 10.7 - Prob. 2ECh. 10.7 - Prob. 3ECh. 10.7 - Prob. 4ECh. 10.7 - Prob. 5ECh. 10.7 - Prob. 6ECh. 10.7 - Prob. 7ECh. 10.7 - Prob. 8ECh. 10.7 - Prob. 9ECh. 10.7 - Prob. 10ECh. 10.7 - Prob. 11ECh. 10.7 - Prob. 12ECh. 10.7 - Prob. 13ECh. 10.7 - Prob. 14ECh. 10.7 - Prob. 15ECh. 10.7 - Prob. 16ECh. 10.7 - Prob. 17ECh. 10.7 - Prob. 18ECh. 10.7 - Prob. 19ECh. 10.7 - Prob. 20ECh. 10.7 - Prob. 21ECh. 10.7 - Prob. 22ECh. 10.7 - Prob. 23ECh. 10.7 - Prob. 24ECh. 10.7 - Prob. 25ECh. 10.7 - Prob. 26ECh. 10.7 - Prob. 27ECh. 10.7 - Prob. 28ECh. 10.7 - Prob. 29ECh. 10.7 - Prob. 30ECh. 10.7 - Prob. 31ECh. 10.7 - Prob. 32ECh. 10.7 - Prob. 33ECh. 10.7 - Prob. 34ECh. 10.7 - Prob. 35ECh. 10.7 - Prob. 36ECh. 10.7 - Prob. 37ECh. 10.7 - Prob. 38ECh. 10.7 - Prob. 39ECh. 10.7 - Prob. 40ECh. 10.7 - Prob. 41ECh. 10.7 - Prob. 42ECh. 10.7 - Prob. 43ECh. 10.7 - Prob. 44ECh. 10.7 - Prob. 45ECh. 10.7 - Prob. 46ECh. 10.7 - Prob. 47ECh. 10.7 - Prob. 48ECh. 10.8 - The system of equations {2yx2=0yx=4 is graphed...Ch. 10.8 - Prob. 2ECh. 10.8 - Prob. 3ECh. 10.8 - Prob. 4ECh. 10.8 - Prob. 5ECh. 10.8 - Prob. 6ECh. 10.8 - Prob. 7ECh. 10.8 - Prob. 8ECh. 10.8 - Prob. 9ECh. 10.8 - Prob. 10ECh. 10.8 - Prob. 11ECh. 10.8 - Prob. 12ECh. 10.8 - Prob. 13ECh. 10.8 - Prob. 14ECh. 10.8 - Prob. 15ECh. 10.8 - Prob. 16ECh. 10.8 - Prob. 17ECh. 10.8 - Prob. 18ECh. 10.8 - Prob. 19ECh. 10.8 - Prob. 20ECh. 10.8 - Prob. 21ECh. 10.8 - Prob. 22ECh. 10.8 - Prob. 23ECh. 10.8 - Prob. 24ECh. 10.8 - Prob. 25ECh. 10.8 - Prob. 26ECh. 10.8 - Prob. 27ECh. 10.8 - Prob. 28ECh. 10.8 - Prob. 29ECh. 10.8 - Prob. 30ECh. 10.8 - Prob. 31ECh. 10.8 - Prob. 32ECh. 10.8 - Prob. 33ECh. 10.8 - Prob. 34ECh. 10.8 - Prob. 35ECh. 10.8 - Prob. 36ECh. 10.8 - Prob. 37ECh. 10.8 - Prob. 38ECh. 10.8 - Prob. 39ECh. 10.8 - Prob. 40ECh. 10.8 - Dimensions of a Rectangle A rectangle has an area...Ch. 10.8 - Legs of a Right Triangle A right triangle has an...Ch. 10.8 - Dimensions of a Rectangle The perimeter of a...Ch. 10.8 - Dimensions of a Rectangle A circular piece of...Ch. 10.8 - Flight of a Rocket A hill is inclined so that its...Ch. 10.8 - Making a Stovepipe A rectangular piece of sheet...Ch. 10.8 - Global Positioning System (GPS) The Global...Ch. 10.8 - Prob. 48ECh. 10.8 - Prob. 49ECh. 10.9 - To graph an inequality, we first graph the...Ch. 10.9 - Prob. 2ECh. 10.9 - Prob. 3ECh. 10.9 - Prob. 4ECh. 10.9 - Prob. 5ECh. 10.9 - Prob. 6ECh. 10.9 - Prob. 7ECh. 10.9 - Prob. 8ECh. 10.9 - Prob. 9ECh. 10.9 - Prob. 10ECh. 10.9 - Prob. 11ECh. 10.9 - Prob. 12ECh. 10.9 - Prob. 13ECh. 10.9 - Prob. 14ECh. 10.9 - Prob. 15ECh. 10.9 - Prob. 16ECh. 10.9 - Prob. 17ECh. 10.9 - Prob. 18ECh. 10.9 - Prob. 19ECh. 10.9 - Prob. 20ECh. 10.9 - Prob. 21ECh. 10.9 - Prob. 22ECh. 10.9 - Prob. 23ECh. 10.9 - Prob. 24ECh. 10.9 - Prob. 25ECh. 10.9 - Prob. 26ECh. 10.9 - Prob. 27ECh. 10.9 - Prob. 28ECh. 10.9 - Prob. 29ECh. 10.9 - Prob. 30ECh. 10.9 - Prob. 31ECh. 10.9 - Prob. 32ECh. 10.9 - Prob. 33ECh. 10.9 - Prob. 34ECh. 10.9 - Prob. 35ECh. 10.9 - Prob. 36ECh. 10.9 - Prob. 37ECh. 10.9 - Prob. 38ECh. 10.9 - Prob. 39ECh. 10.9 - Prob. 40ECh. 10.9 - Prob. 41ECh. 10.9 - Prob. 42ECh. 10.9 - Prob. 43ECh. 10.9 - Prob. 44ECh. 10.9 - Prob. 45ECh. 10.9 - Prob. 46ECh. 10.9 - Prob. 47ECh. 10.9 - Prob. 48ECh. 10.9 - Prob. 49ECh. 10.9 - Prob. 50ECh. 10.9 - Prob. 51ECh. 10.9 - Prob. 52ECh. 10.9 - Coffee Blends A coffee merchant sells two...Ch. 10.9 - Nutrition A cat food manufacturer uses fish and...Ch. 10.9 - Prob. 55ECh. 10 - Prob. 1RCCCh. 10 - Prob. 2RCCCh. 10 - Prob. 3RCCCh. 10 - Prob. 4RCCCh. 10 - Prob. 5RCCCh. 10 - Prob. 6RCCCh. 10 - Prob. 7RCCCh. 10 - Prob. 8RCCCh. 10 - Prob. 9RCCCh. 10 - Prob. 10RCCCh. 10 - Prob. 11RCCCh. 10 - Prob. 12RCCCh. 10 - Prob. 13RCCCh. 10 - Prob. 14RCCCh. 10 - Prob. 15RCCCh. 10 - Prob. 16RCCCh. 10 - Prob. 17RCCCh. 10 - Prob. 18RCCCh. 10 - Prob. 19RCCCh. 10 - Prob. 1RECh. 10 - Prob. 2RECh. 10 - Prob. 3RECh. 10 - Prob. 4RECh. 10 - Prob. 5RECh. 10 - Prob. 6RECh. 10 - Prob. 7RECh. 10 - Prob. 8RECh. 10 - Prob. 9RECh. 10 - Prob. 10RECh. 10 - Prob. 11RECh. 10 - Prob. 12RECh. 10 - Prob. 13RECh. 10 - Prob. 14RECh. 10 - Prob. 15RECh. 10 - Prob. 16RECh. 10 - Prob. 17RECh. 10 - Prob. 18RECh. 10 - Prob. 19RECh. 10 - Prob. 20RECh. 10 - Prob. 21RECh. 10 - Prob. 22RECh. 10 - Prob. 23RECh. 10 - Prob. 24RECh. 10 - Prob. 25RECh. 10 - Prob. 26RECh. 10 - Prob. 27RECh. 10 - Prob. 28RECh. 10 - Prob. 29RECh. 10 - Prob. 30RECh. 10 - Prob. 31RECh. 10 - Prob. 32RECh. 10 - Prob. 33RECh. 10 - Prob. 34RECh. 10 - Prob. 35RECh. 10 - Prob. 36RECh. 10 - Prob. 37RECh. 10 - Prob. 38RECh. 10 - Prob. 39RECh. 10 - Prob. 40RECh. 10 - Prob. 41RECh. 10 - Prob. 42RECh. 10 - Prob. 43RECh. 10 - Prob. 44RECh. 10 - Prob. 45RECh. 10 - Prob. 46RECh. 10 - Prob. 47RECh. 10 - Prob. 48RECh. 10 - Prob. 49RECh. 10 - Prob. 50RECh. 10 - Prob. 51RECh. 10 - Prob. 52RECh. 10 - Prob. 53RECh. 10 - Prob. 54RECh. 10 - Prob. 55RECh. 10 - Prob. 56RECh. 10 - Prob. 57RECh. 10 - Prob. 58RECh. 10 - Prob. 59RECh. 10 - Prob. 60RECh. 10 - Prob. 61RECh. 10 - Prob. 62RECh. 10 - Prob. 63RECh. 10 - Prob. 64RECh. 10 - Prob. 65RECh. 10 - Prob. 66RECh. 10 - Prob. 67RECh. 10 - Prob. 68RECh. 10 - Prob. 69RECh. 10 - Prob. 70RECh. 10 - Prob. 71RECh. 10 - Prob. 72RECh. 10 - Prob. 73RECh. 10 - Prob. 74RECh. 10 - Prob. 75RECh. 10 - Prob. 76RECh. 10 - Prob. 77RECh. 10 - Prob. 78RECh. 10 - Prob. 79RECh. 10 - Prob. 80RECh. 10 - Prob. 81RECh. 10 - Prob. 82RECh. 10 - Prob. 83RECh. 10 - Prob. 84RECh. 10 - Prob. 85RECh. 10 - Prob. 86RECh. 10 - Prob. 87RECh. 10 - Prob. 88RECh. 10 - Prob. 89RECh. 10 - Prob. 90RECh. 10 - Prob. 91RECh. 10 - Prob. 92RECh. 10 - Prob. 93RECh. 10 - Prob. 94RECh. 10 - Prob. 95RECh. 10 - Prob. 96RECh. 10 - Prob. 97RECh. 10 - Prob. 98RECh. 10 - Prob. 99RECh. 10 - Prob. 100RECh. 10 - Prob. 101RECh. 10 - Prob. 102RECh. 10 - Prob. 103RECh. 10 - Prob. 104RECh. 10 - Prob. 105RECh. 10 - Prob. 106RECh. 10 - Prob. 107RECh. 10 - Prob. 108RECh. 10 - Prob. 109RECh. 10 - Prob. 110RECh. 10 - Prob. 111RECh. 10 - Prob. 112RECh. 10 - Prob. 1TCh. 10 - Prob. 2TCh. 10 - Prob. 3TCh. 10 - Prob. 4TCh. 10 - Prob. 5TCh. 10 - Prob. 6TCh. 10 - Prob. 7TCh. 10 - Anne, Barry, and Cathy enter a coffee shop. Anne...Ch. 10 - Prob. 9TCh. 10 - Prob. 10TCh. 10 - Only one of the following matrices has an inverse....Ch. 10 - Prob. 12TCh. 10 - Prob. 13TCh. 10 - Prob. 14TCh. 10 - Find the maximum and minimum values of the given...Ch. 10 - Prob. 2PCh. 10 - Prob. 3PCh. 10 - Find the maximum and minimum value of the given...Ch. 10 - Making Furniture A furniture manufacturer makes...Ch. 10 - A Housing Development A housing contractor has...Ch. 10 - Hauling Fruit A trucker hauls citrus fruit from...Ch. 10 - Manufacturing Calculators A manufacturer of...Ch. 10 - Shipping Televisions An electronics discount chain...Ch. 10 - Prob. 10PCh. 10 - Packaging Nuts A confectioner sells two types of...Ch. 10 - Feeding Lab Rabbits A biologist wishes to feed...Ch. 10 - Investing in Bonds A woman wishes to invest 12,000...Ch. 10 - Prob. 14PCh. 10 - Business Strategy A small software company...Ch. 10 - Feasible Region All parts of this problem refer to...
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Solve ANY Optimization Problem in 5 Steps w/ Examples. What are they and How do you solve them?; Author: Ace Tutors;https://www.youtube.com/watch?v=BfOSKc_sncg;License: Standard YouTube License, CC-BY
Types of solution in LPP|Basic|Multiple solution|Unbounded|Infeasible|GTU|Special case of LP problem; Author: Mechanical Engineering Management;https://www.youtube.com/watch?v=F-D2WICq8Sk;License: Standard YouTube License, CC-BY
Optimization Problems in Calculus; Author: Professor Dave Explains;https://www.youtube.com/watch?v=q1U6AmIa_uQ;License: Standard YouTube License, CC-BY
Introduction to Optimization; Author: Math with Dr. Claire;https://www.youtube.com/watch?v=YLzgYm2tN8E;License: Standard YouTube License, CC-BY