Chapter 10, Problem 16P

Feasible Region All parts of this problem refer to the following feasible region and objective function.

$\begin{array}{r}\hfill \{\begin{array}{c}x\ge 0\\ x\ge y\\ x+2y\ge 12\\ x+y\le 10\end{array}\\ \hfill P=x+4y\end{array}$

1. (a) Graph the feasible region.
2. (b) On your graph from part (a), sketch the graphs of the linear equations obtained by setting P equal to 40, 36, 32, and 28.
3. (c) If you continue to decrease the value of P, at which vertex of the feasible region will these lines first touch the feasible region?
4. (d) Verify that the maximum value of P on the feasible region occurs at the vertex you chose in part (c).

To determine

To sketch: The graph of the given feasible region and the objective function.

Explanation of Solution

The given feasible region with the objective function is,

$\{\begin{array}{c}x\ge 0\\ x\ge y\\ x+2y\ge 12\\ x+y\le 10\end{array}$ (1)

The Production function is,

$P=x+4y$

Now, take the equalities of the equation (1), $x=0$

And, $x=y$ (2)

And, $x+2y=12$ (3)

And, $x+y=10$ (4)

Substitute y for x in the equation (3),

$\begin{array}{c}y+2y=12\\ 3y=12\\ y=\frac{12}{3}\\ y=4\end{array}$

Substitute 4 for x in the equation (2),

$y=4$.

The intersection point is $\left(x,y\right)=\left(4,4\right)$.

Substitute $x$ for y in the equation (4).

$\begin{array}{c}x+y=10\\ x+x=10\\ 2x=10\\ x=5\end{array}$

Substitute 5 for x in the equation (2),

$y=5$

Thus, the intersection point is $\left(x,y\right)=\left(5,5\right)$.

Now, get the value of y in terms of x from the equation (4),

$y=10-x$ (5)

Substitute $10-x$ for y in equation (3),

$\begin{array}{c}x+2y=12\\ x+2\left(10-x\right)=12\\ x+20-2x=12\\ -x=-8\end{array}$

Further solve the above equation

$x=8$

Substitute 8 for x in equation (5),

$\begin{array}{c}y=10-8\\ y=2\end{array}$

The intersection point is $\left(x,y\right)=\left(8,2\right)$.

Now, draw the graph of the above equations,

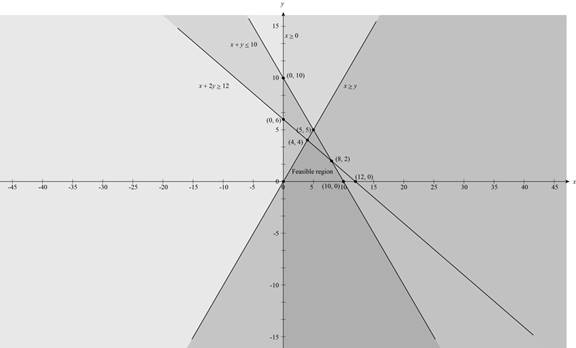
Figure (1)

Thus, the vertices which lies in the feasible region is $\left(10,0\right)$, $\left(0,0\right)$, $\left(4,4\right)$, $\left(8,2\right)$

To determine

To sketch: The graph at the fix value of $P=40$, $P=32$, $P=36$, and $P=28$ in the  objective function $P=x+4y$ from the part (a).

Explanation of Solution

The given feasible region with the objective function is,

$\{\begin{array}{c}x\ge 0\\ x\ge y\\ x+2y\ge 12\\ x+y\le 10\end{array}$ (1)

The Production function is,

$P=x+4y$,

Substitute 40 for P in the equation production function $P=x+4y$,

$\begin{array}{c}P=x+4y\\ x+4y=40\end{array}$

Substitute 36 for P in the equation production function $P=x+4y$,

$\begin{array}{c}P=x+4y\\ x+4y=36\end{array}$

Substitute 32 for P in the equation production function $P=x+4y$,

$\begin{array}{c}P=x+4y\\ x+4y=32\end{array}$

Substitute 28 for P in the equation production function $P=x+4y$,

$\begin{array}{c}P=x+4y\\ x+4y=28\end{array}$

Now, draw the graph of the above equations,

Figure (2)

Figure (2) shows the graph at points 40, 36, 32 and 28.

To determine

To find: The vertex at which the value of P keeps decreases and first touch the line of the feasible region.

Answer to Problem 16P

The vertex at which the value of P keeps decreases and first touches the line of the feasible region. is $\left(4,4\right)$.

Explanation of Solution

Given:

The given feasible region with the objective function is,

$\{\begin{array}{c}x\ge 0\\ x\ge y\\ x+2y\ge 12\\ x+y\le 10\end{array}$ (1)

The Production function is,

$P=x+4y$,

From the graph part (b), the value of the P decreases with respect to the line $P=x+4y$ and somewhere it touches or intersects the point $\left(4,4\right)$ on the line $x+2y=12$.

Thus, the vertex at which the value of P keeps decreases and first touches the line of the feasible region. is $\left(4,4\right)$.

To determine

To verify: The maximum value of P on the feasible region occurs at the point $\left(4,4\right)$.

Explanation of Solution

Proof:

The given feasible region with the objective function is,

$\{\begin{array}{c}x\ge 0\\ x\ge y\\ x+2y\ge 12\\ x+y\le 10\end{array}$ (1)

The Production function is,

$P=x+4y$,

The vertices which lies in the feasible region is $\left(10,0\right)$, $\left(0,0\right)$, $\left(4,4\right)$, $\left(8,2\right)$ in the graph of the given constraints shown in figure (1) of part (a).

Vertices	$P=x+4y$
$\left(0,0\right)$	$\begin{array}{c}P=0+4\cdot 0\\ =0\end{array}$
$\left(10,0\right)$	$\begin{array}{c}P=10+4\cdot 0\\ =10\end{array}$
$\left(4,4\right)$	$\begin{array}{c}P=4+4\cdot 4\\ =20\end{array}$(Maximum)
$\left(8,2\right)$	$\begin{array}{c}P=8+4\cdot 2\\ =16\end{array}$

Hence, the maximum value of $P=x+4y$ is 20 occurred at $\left(4,4\right)$.