Chapter 10, Problem 10.73P

Interpretation Introduction

(a)

Interpretation:

The liquidus temperature for $\text{MgO-65 wt\% FeO}$ ceramic is to be determined at equilibrium conditions.

Concept Introduction:

On the temperature-composition graph of a ceramic, the curve above which the ceramic exist in the liquid phase is the liquidus curve. The temperature at this curve is maximum known as liquidus temperature at which the crystals in the ceramic can coexist with its melt in the thermodynamic equilibrium.

Answer to Problem 10.73P

Liquidus temperature, $T_L={2000}^{\circ }\text{C}$

Explanation of Solution

The equilibrium phase diagram for the MgO-FeO system is shown below as:

A straight line from $\text{MgO-65 wt\% FeO}$ is drawn as shown.

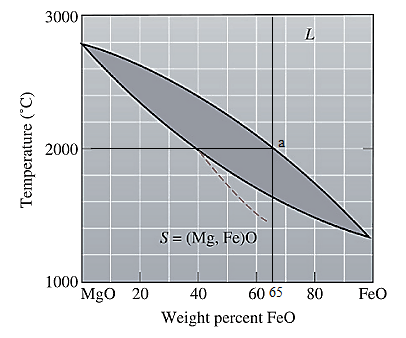
Liquidus temperature $\left(T_L\right)$ is represented by point 'a' where the line touches the upper curve.

  $T_L={2000}^{\circ }\text{C}$

Interpretation Introduction

(b)

Interpretation:

The solidus temperature for $\text{MgO-65 wt\% FeO}$ ceramic is to be determined.

Concept Introduction:

Solidus curve is the locus of the temperature on the temperature composition graph of a ceramic, beyond which the ceramic is completely in solid phase. The temperature at this curve is minimum known as solidus temperature at which the crystals in the ceramic can coexist with its melt in the thermodynamic equilibrium.

Answer to Problem 10.73P

Solidus temperature, $T_S={1620}^{\circ }\text{C}$

Explanation of Solution

The equilibrium phase diagram for the MgO-FeO system is shown below as:

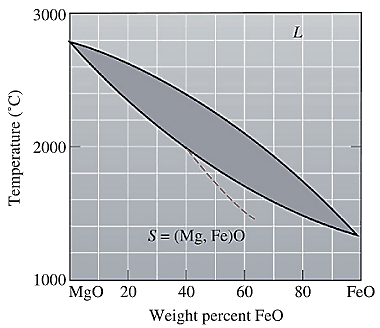
A straight line from $\text{MgO-65 wt\% FeO}$ is drawn as shown.

Solidus temperature $\left(T_S\right)$ is represented by point 'b' where the line touches the lower curve.

  $T_S={1620}^{\circ }\text{C}$

Interpretation Introduction

(c)

Interpretation:

The freezing range for $\text{MgO-65 wt\% FeO}$ ceramic is to be determined.

Concept Introduction:

Freezing range for a ceramic is the difference of the liquidus and the solidus temperature of a ceramic. In this range, the ceramic melt starts to crystallize at liquidus temperature and solidifies when reaches solidus temperature.

Answer to Problem 10.73P

Freezing range, $\text{FR}={380}^{\circ }\text{C}$

Explanation of Solution

From part (a) and (b), the liquidus and solidus temperature for the given ceramic is determined as:

  $\begin{array}{c}{T}_L={2000}^{\circ }\text{C}\\ T_S={1620}^{\circ }\text{C}\end{array}$

The freezing range (FR) for this ceramic composition will be:

  $\begin{array}{c}\text{FR}=T_L-T_S\\ =2000-1620\\ ={380}^{\circ }\text{C}\end{array}$

Interpretation Introduction

(d)

Interpretation:

The composition of the first solid that is formed when $\text{MgO-65 wt\% FeO}$ ceramic is cooled is to be determined.

Concept Introduction:

On the temperature-composition graph of a ceramic, the curve above which the ceramic exist in the liquid phase is the liquidus curve. The temperature at this curve is maximum known as liquidus temperature at which the crystals in the ceramic can coexist with its melt in the thermodynamic equilibrium.

Answer to Problem 10.73P

The composition of the first solid formed is $S_{\text{first}}=38\text{ wt\% FeO}$.

Explanation of Solution

The equilibrium phase diagram for the MgO-FeO system is shown below as:

A straight line from $\text{MgO-65 wt\% FeO}$ is drawn as shown below. Where this line touches the liquidus curve, first solid appears. Draw a horizontal straight line to point 'a'.

Point 'a' represents the composition of the first solid which is formed when $\text{MgO-65 wt\% FeO}$ is cooled.

  $S_{\text{first}}=38\text{ wt\% FeO}$

Interpretation Introduction

(e)

Interpretation:

The composition of the last liquid which is solidified when $\text{MgO-65 wt\% FeO}$ ceramic is cooled is to be determined.

Concept Introduction:

On the temperature-composition graph of a ceramic, the curve above which the ceramic exist in the liquid phase is the liquidus curve. The temperature at this curve is maximum known as liquidus temperature at which the crystals in the ceramic can coexist with its melt in the thermodynamic equilibrium.

Solidus curve is the locus of the temperature on the temperature composition graph of a ceramic, beyond which the ceramic is completely in solid phase.

Between the solidus and liquidus curve, the ceramic exits in a slurry form in which there is both crystals as well as ceramic melt.

Solidus temperature is always less than or equal to the liquidus temperature.

Answer to Problem 10.73P

The composition of the last liquid solidified is $L_{\text{last}}=85\text{ wt\% FeO}$.

Explanation of Solution

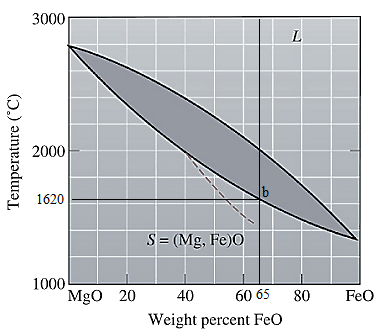
The equilibrium phase diagram for the MgO-FeO system is shown below as:

A straight line from $\text{MgO-65 wt\% FeO}$ is drawn as shown below. Where this line touches the solidus curve, last liquid solidifies. Draw a horizontal straight line to point 'b'.

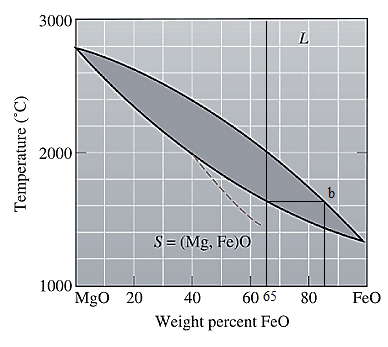
Point 'b' represents the composition of the last liquid which solidify when $\text{MgO-65 wt\% FeO}$ is cooled.

  $L_{\text{last}}=85\text{ wt\% FeO}$

Interpretation Introduction

(f)

Interpretation:

The phases present, their compositions and their amounts for $\text{MgO-65 wt\% FeO}$ ceramic at ${1800}^{\circ }\text{C}$ are to be determined.

Concept Introduction:

On the temperature-composition graph of a ceramic, the curve above which the ceramic exist in the liquid phase is the liquidus curve. The temperature at this curve is the maximum temperature at which the crystals in the ceramic can coexist with its melt in the thermodynamic equilibrium.

Solidus curve is the locus of the temperature on the temperature composition graph of a ceramic, beyond which the ceramic is completely in solid phase.

Between the solidus and liquidus curve, the ceramic exits in a slurry form in which there is both crystals as well as ceramic melt.

Solidus temperature is always less than or equal to the liquidus temperature.

Amount of each phase in wt% is calculated using lever rule. At a particular temperature and ceramic composition, a tie line is drawn on the phase diagram of the ceramic between the solidus and liquidus curve. Then the portion of the lever opposite to the phase whose amount is to be calculated is considered in the formula used as:

  $\text{Phase wt\%}=\frac{\text{opposite arm of lever}}{\text{total length of the tie line}}\times 100$ ...... (1)

Answer to Problem 10.73P

Both solid as well as liquid phases are present at the given conditions.

Composition of the liquid phase present is $53\text{ wt\% FeO}$.

Composition of the solid phase present is $78\text{ wt\% FeO}$.

Amount of the liquid phase is $52\%$.

Amount of the solid phase is $48\%$.

Explanation of Solution

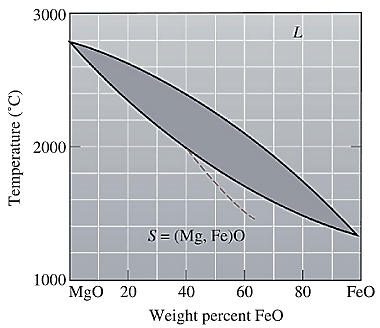
The equilibrium phase diagram for the MgO-FeO system is shown below as:

Now, draw a straight line from $\text{MgO-65 wt\% FeO}$ ceramic composition at ${1800}^{\circ }\text{C}$ as shown below:

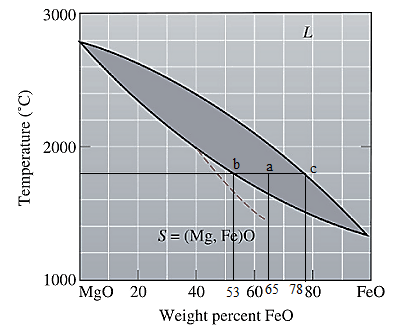
Both the phases, solid and liquid are present at this condition. Point 'b' represents the liquid phase composition in wt% and point 'c' represents the solid phase composition in wt%. From the above phase diagram:

  $\begin{array}{c}L=53\text{ wt\% FeO}\\ S=78\text{ wt\% FeO}\end{array}$

To calculate amount of liquid phase, lever 'ac' will be used and to calculate amount of solid phase, lever 'ba' will be used. Use equation (1) to calculate the amount of each phase as:

  $\begin{array}{c}\text{Liquid wt\%}=\frac{\text{length of 'ac'}}{\text{length of 'bc'}}\times 100\\ =\frac{78-65}{78-53}\times 100\\ =52\text{ wt}\%\\ \text{Solid wt\%}=\frac{\text{length of 'ba'}}{\text{length of 'bc'}}\times 100\\ =\frac{65-53}{78-53}\times 100\\ =48\text{ wt}\%\end{array}$

Interpretation Introduction

(g)

Interpretation:

The phases present, their compositions and their amounts for $\text{MgO-65 wt\% FeO}$ ceramic at ${1600}^{\circ }\text{C}$ are to be determined.

Concept Introduction:

On the temperature-composition graph of a ceramic, the curve above which the ceramic exist in the liquid phase is the liquidus curve. The temperature at this curve is the maximum temperature at which the crystals in the ceramic can coexist with its melt in the thermodynamic equilibrium.

Solidus curve is the locus of the temperature on the temperature composition graph of a ceramic, beyond which the ceramic is completely in solid phase.

Between the solidus and liquidus curve, the ceramic exits in a slurry form in which there is both crystals as well as ceramic melt.

Solidus temperature is always less than or equal to the liquidus temperature.

Amount of each phase in wt% is calculated using lever rule. At a particular temperature and ceramic composition, a tie line is drawn on the phase diagram of the ceramic between the solidus and liquidus curve. Then the portion of the lever opposite to the phase whose amount is to be calculated is considered in the formula used as:

  $\text{Phase wt\%}=\frac{\text{opposite arm of lever}}{\text{total length of the tie line}}\times 100$ ...... (1)

Answer to Problem 10.73P

  $100\%$ Solid phase

Explanation of Solution

The equilibrium phase diagram for the MgO-FeO system is shown below as:

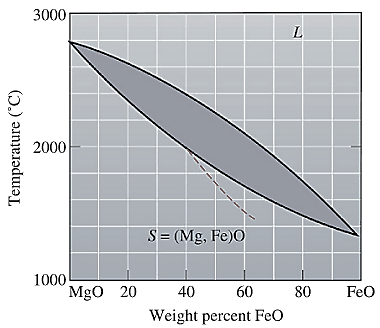
Now, draw a straight line from $\text{MgO-65 wt\% FeO}$ ceramic composition at ${1600}^{\circ }\text{C}$ as shown below:

At this point 'a', only one phase is present which is solid, and it has $100\%$ composition.