
(a)
Interpretation:
The composition of the solid phase and the liquid phase in mol% and wt% are to be calculated for
Concept Introduction:
On the temperature-composition graph of a ceramic, the curve above which the ceramic exist in the liquid phase is the liquidus curve. The temperature at this curve is the maximum temperature at which the crystals in the ceramic can coexist with its melt in the
Solidus curve is the locus of the temperature on the temperature composition graph of a ceramic, beyond which the ceramic is completely in solid phase.
Between the solidus and liquidus curve, the ceramic exits in a slurry form in which there is both crystals as well as ceramic melt.
Solidus temperature is always less than or equal to the liquidus temperature.
The formula to calculate the wt% from the mol% for a ceramic containing phases
Here,
Answer to Problem 10.53P
Composition of the liquid phase in mol% is
Composition of the liquid phase in wt% is
Composition of the solid phase in mol% is
Composition of the solid phase in wt% is
Explanation of Solution
The phase diagram for NiO-MgO is given as:
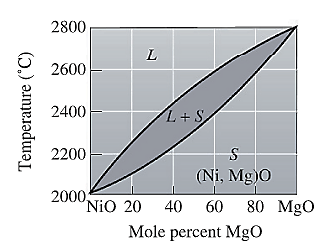
Now, draw a straight line from temperature
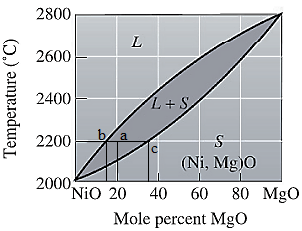
Here, point 'a' represents
Molecular weight of NiO and MgO are
Use equation (1) to convert mol% to wt% for liquid phase as:
Again, use equation (1) to convert mol% to wt% for solid phase as:
(b)
Interpretation:
The amount of each phase present in
Concept Introduction:
A matter can exist in different physical forms such as sold, liquid, gas, and plasma. These distinct physical forms are known as a Phase.
A phase has uniform physical and chemical properties and is bounded by a surface due to which two phases can be
The formula to calculate the wt% from the mol% for a ceramic containing phases
Here,
Amount of each phase in mol% is calculated using lever rule. At a particular temperature and ceramic composition, a tie line is drawn on the phase diagram of the ceramic between the solidus and liquidus curve. Then the portion of the lever opposite to the phase whose amount is to be calculated is considered in the formula used as:
Answer to Problem 10.53P
Amount of liquid phase in mol% is
Amount of liquid phase in wt% is
Amount of solid phase in mol% is
Amount of solid phase in wt% is
Explanation of Solution
The phase diagram for NiO-MgO is given as:
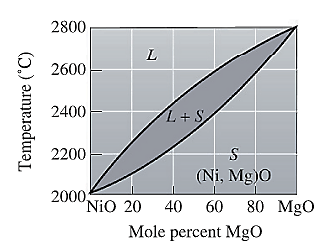
Now, draw a straight line from temperature
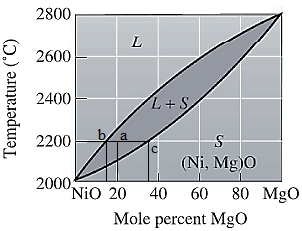
Here, point 'a' represents
To calculate amount of liquid phase, lever 'ac' will be used and to calculate amount of solid phase, lever 'ba' will be used. Use equation (2) to calculate the amount of each phase as:
To calculate the amount of liquid and solid phases in wt%, first convert the original mol% of MgO in wt% using equation (1) and molecular weights of NiO and MgO as:
To apply the lever rule, use the corresponding wt% for the liquid and solid phases as calculated in part (a) as:
Apply lever rule as:
(c)
Interpretation:
The amount of each phase is to be calculated in vol%.
Concept Introduction:
The formula to convert wt% to vol% using density
Answer to Problem 10.53P
The amount of liquid phase in vol% is
The amount of solid phase in vol% is
Explanation of Solution
Given information:
A ceramic containing
From part (b), the amount of liquid and solid phases in wt% is calculated as:
Use equation (3) along with the given densities of the phases to calculate the vol% as:
Want to see more full solutions like this?
Chapter 10 Solutions
Essentials of Materials Science and Engineering, SI Edition
- Based on the results obtained, comment on the relative importance of the body and the tails of thedistributions of R and S on the probability of failure with increasing central safety factor CSF .arrow_forwardFind Vo using mesh analysisarrow_forwardThe resistance R and load effect S for a given failure mode are statistically independent random variables with marginal PDF's 1 fR (r) = 0≤r≤100 100' fs(s)=0.05e-0.05s (a) Determine the probability of failure by computing the probability content of the failure domain defined as {rarrow_forward1. The beam is supported by a roller constraint at B, which allows vertical displacement but resists axial load and moment. If the bar is subjected to the loading shown and constant El (L = 12 ft, E = 3100 ksi, I = 1728 in (rectangular section 12"x12"), w = 1 klf). Caution: pay attention to unit conversion between ft and in) x W B a. Sketch the deflected shape. L b. Determine the equations of the slope and the elastic curve using the coordinate x. First, solve this problem parametrically, and then substitute the numerical values for L, E, I, w at the end. There will be a significant penalty for solutions that do not calculate the slope and deflection as parametric functions. c. Specify the slope (in radians) at point A (parametrically and numerically). d. Specify the vertical displacement at point B (parametrically and numerically).arrow_forward4. EI is constant in the beam below (a = 12 ft, b = 5 ft, E = 29,000 ksi, I = 800 in¹ (W18x50), P = 2 kip): b Р C a. Sketch the deflected shape. b. Determine the equations of the slope and the elastic curve using the coordinates x1 and x2. c. For the AB segment, determine the maximum deflection and its location. Hint: at maximum deflection, the slope is zero. d. Specify the slope (in radians) and deflection at point C.arrow_forward3. EI is constant in the beam below (a = 10 ft, b = 5 ft, E = 29,000 ksi, I = 340 in (W14x34), Mo = 50 k. ft): Mo Mo a. Sketch the deflected shape. X2 b. Determine the equations of the slope and the elastic curve using the coordinates x1 and x2. Due to symmetry, only the left side is sufficient. Hint: symmetry requires the slope to be zero at mid span. c. Determine the maximum deflection. d. Specify the slope (in radians) at point A.arrow_forward2. EI is constant in the beam below (L = 10 ft, E = 29,000 ksi, I = 350 in (W12x45), W = 500 lb/ft): a. Sketch the deflected shape. b. Determine the equations of the slope and the elastic curve using the coordinates x1 and X2. c. Specify the slope (in radians) and deflection at point C. d. Specify the slope (in radians) at point B. -x- L 2 W C X27 L 22 Barrow_forwardPlease solve this problem as soon as possible My ID# 016948724arrow_forwardRead the paper of Khalili et al. (2004). Describe the issue raised by Jennings and Burland in using the single-value effective stress to quantify the problem of wetting-induced collapse. Use the discussion in Khalili et al. (2004) on the different ways that effective stress and yield stress change with suction to explain how wetting-induced collapse can be modeled with the single-valued effective stress. Comment on whether the soil tested by Jotisankasa (2003) would be collapsible based on the discussionarrow_forwardc) An RC circuit is given in Figure Q1.1, where Vi(t) and Vo(t) are the input and output voltages. (i) Derive the transfer function of the circuit. (ii) With a unit step change of Vi(t) applied to the circuit, derive the time response of Vo(t) with this step change. Vi(t) C₁ Vo(1) R₂ C2 C3 | R = 20 ΚΩ = 50 ΚΩ C=C2=C3=25 μF Figure Q1.1. RC circuit.arrow_forwardc) An RC circuit is given in Figure Q1. vi(t) and vo (t) are the input and output voltages. (i) Derive the transfer function of the circuit. (ii) With a unit step change vi(t) applied to the circuit, derive and sketch the time response of the circuit. R₁ R2 v₁(t) R3 C₁ v₁(t) R₁ = R₂ = 10 k R3 = 100 kn C₁ = 100 μF Figure Q1. RC circuit.arrow_forwardc) A RC circuit is given in Figure Q1.1. Vi(t) and Vo(t) are the input and output voltages. (i) Derive the transfer function of the circuit. (ii) With a unit step change of Vi(t) applied to the circuit, derive the time response of the circuit. C₁ C₂ Vi(t) Vo(1) R₁ C₂ R-25 k C=C2=50 µF Figure Q1.1. RC circuit.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 MATLAB: An Introduction with ApplicationsEngineeringISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsEngineeringISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Essentials Of Materials Science And EngineeringEngineeringISBN:9781337385497Author:WRIGHT, Wendelin J.Publisher:Cengage,
Essentials Of Materials Science And EngineeringEngineeringISBN:9781337385497Author:WRIGHT, Wendelin J.Publisher:Cengage, Industrial Motor ControlEngineeringISBN:9781133691808Author:Stephen HermanPublisher:Cengage Learning
Industrial Motor ControlEngineeringISBN:9781133691808Author:Stephen HermanPublisher:Cengage Learning Basics Of Engineering EconomyEngineeringISBN:9780073376356Author:Leland Blank, Anthony TarquinPublisher:MCGRAW-HILL HIGHER EDUCATION
Basics Of Engineering EconomyEngineeringISBN:9780073376356Author:Leland Blank, Anthony TarquinPublisher:MCGRAW-HILL HIGHER EDUCATION Structural Steel Design (6th Edition)EngineeringISBN:9780134589657Author:Jack C. McCormac, Stephen F. CsernakPublisher:PEARSON
Structural Steel Design (6th Edition)EngineeringISBN:9780134589657Author:Jack C. McCormac, Stephen F. CsernakPublisher:PEARSON Fundamentals of Materials Science and Engineering...EngineeringISBN:9781119175483Author:William D. Callister Jr., David G. RethwischPublisher:WILEY
Fundamentals of Materials Science and Engineering...EngineeringISBN:9781119175483Author:William D. Callister Jr., David G. RethwischPublisher:WILEY





