Chapter 10, Problem 10.80P

Interpretation Introduction

(a)

Interpretation:

The liquidus temperature for $\text{Nb-80 wt\% W}$ alloy is to be determined at non-equilibrium conditions.

Concept Introduction:

On the temperature-composition graph of an alloy, the curve above which the alloy exists in the liquid phase is the liquidus curve. The temperature at this curve is at maximum and is known as liquidus temperature. In it, the crystals in the alloy can coexist with its melt in the thermodynamic equilibrium.

Answer to Problem 10.80P

Liquidus temperature, $T_L={3100}^{\circ }\text{C}$

Explanation of Solution

The equilibrium phase diagram for the Nb-W system is shown below as:

A straight line from $\text{Nb-80 wt\% W}$ is drawn as shown.

Liquidus temperature $\left(T_L\right)$ is represented by point 'a' where the line touches the upper curve.

  $T_L={3100}^{\circ }\text{C}$

Interpretation Introduction

(b)

Interpretation:

The solidus temperature for $\text{Nb-80 wt\% W}$ alloy is to be determined at non-equilibrium conditions.

Concept Introduction:

Solidus curve is the locus of the temperature on the temperature composition graph of an alloy, beyond which the alloy is completely in a solid phase. The temperature at this curve is minimum known as solidus temperature at which the crystals in the alloy can coexist with its melt in the thermodynamic equilibrium.

Answer to Problem 10.80P

Solidus temperature, $T_S={2720}^{\circ }\text{C}$

Explanation of Solution

The equilibrium phase diagram for the Nb-W system is shown below as:

A straight line from $\text{Nb-80 wt\% W}$ is drawn till the dashed line which shows the non-equilibrium conditions as shown.

Solidus temperature $\left(T_S\right)$ is represented by point 'b' where the line touches the dashed curve.

  $T_S={2720}^{\circ }\text{C}$

Interpretation Introduction

(c)

Interpretation:

The freezing range for $\text{Nb-80 wt\% W}$ alloy is to be determined.

Concept Introduction:

Freezing range for an alloy is the difference of the liquidus and the solidus temperature of an alloy. In this range, the alloy melt starts to crystallize at liquidus temperature and solidifies when reaches solidus temperature.

Answer to Problem 10.80P

Freezing range, $\text{FR}={380}^{\circ }\text{C}$

Explanation of Solution

From part (a) and (b), the liquidus and solidus temperature for the given alloy is determined as:

  $\begin{array}{c}{T}_L={3100}^{\circ }\text{C}\\ T_S={2720}^{\circ }\text{C}\end{array}$

The freezing range (FR) for this alloy composition will be:

  $\begin{array}{c}\text{FR}=T_L-T_S\\ =3100-2720\\ ={380}^{\circ }\text{C}\end{array}$

Interpretation Introduction

(d)

Interpretation:

The composition of the first solid that is formed when $\text{Nb-80 wt\% W}$ alloy is cooled is to be determined.

Concept Introduction:

On the temperature-composition graph of an alloy, the curve above which the alloy exists in the liquid phase is the liquidus curve. The temperature at this curve is maximum known as liquidus temperature at which the crystals in the alloy can coexist with its melt in the thermodynamic equilibrium.

Answer to Problem 10.80P

The composition of the first solid formed is $S_{\text{first}}=92\text{ wt\% W}$.

Explanation of Solution

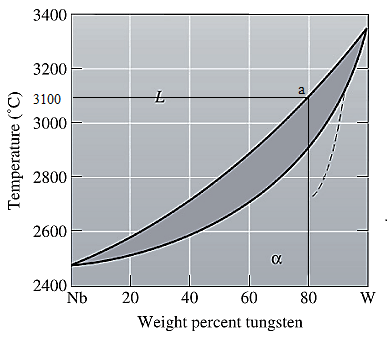
The equilibrium phase diagram for the Nb-W system is shown below as:

A straight line from $\text{Nb-80 wt\% W}$ is drawn as shown below. Where this line touches the liquidus curve, first solid appears. Draw a horizontal straight line to point 'a'.

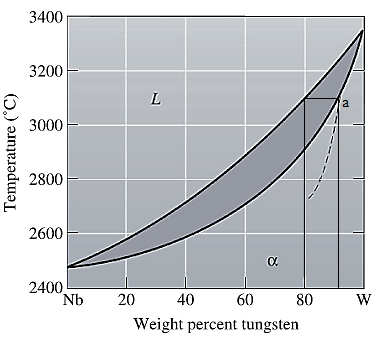
Point 'a' represents the composition of the first solid which is formed when $\text{Nb-80 wt\% W}$ is cooled.

  $S_{\text{first}}=92\text{ wt\% W}$

Interpretation Introduction

(e)

Interpretation:

The composition of the last liquid which is solidified when $\text{Nb-80 wt\% W}$ alloy is cooled is to be determined.

Concept Introduction:

On the temperature-composition graph of an alloy, the curve above which the alloy exists in the liquid phase is the liquidus curve. The temperature at this curve is at maximum, is known as liquidus temperature at which the crystals in the alloy can coexist with its melt in the thermodynamic equilibrium.

Solidus curve is the locus of the temperature on the temperature composition graph of an alloy, beyond which the alloy is completely in a solid phase.

Between the solidus and liquidus curve, the alloy exits in a slurry form in which there is both crystals as well as alloy melt.

Solidus temperature is always less than or equal to the liquidus temperature.

Answer to Problem 10.80P

The composition of the last liquid solidified is $L_{\text{last}}=42\text{ wt\% W}$.

Explanation of Solution

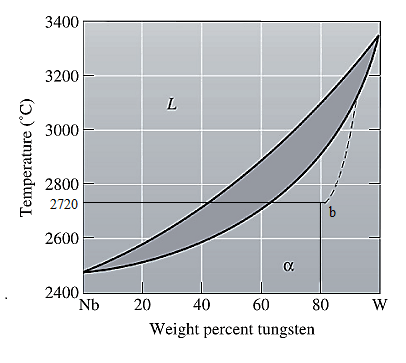
The equilibrium phase diagram for the Nb-W system is shown below as:

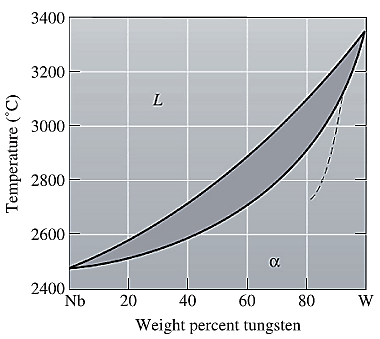
A straight line from $\text{Nb-80 wt\% W}$ is drawn as shown below. Where this line touches the dashed solidus curve, last liquid solidifies in non-equilibrium conditions. Draw a horizontal straight line to point 'b'.

Point 'b' represents the composition of the last liquid which solidifies when $\text{Nb-80 wt\% W}$ is cooled.

  $L_{\text{last}}=42\text{ wt\% W}$

Interpretation Introduction

(f)

Interpretation:

The phases present, their compositions and their amounts for $\text{Nb-80 wt\% W}$ alloy at ${3000}^{\circ }\text{C}$ are to be determined.

Concept Introduction:

On the temperature-composition graph of an alloy, the curve above which the alloy exists in the liquid phase is the liquidus curve. The temperature at this curve is the maximum temperature at which the crystals in the alloy can coexist with its melt in the thermodynamic equilibrium.

Solidus curve is the locus of the temperature on the temperature composition graph of an alloy, beyond which the alloy is completely in a solid phase.

Between the solidus and liquidus curve, the alloy exits in a slurry form in which there is both crystals as well as alloy melt.

Solidus temperature is always less than or equal to the liquidus temperature.

Amount of each phase in wt% is calculated using lever rule. At a particular temperature and alloy composition, a tie line is drawn on the phase diagram of the alloy between the solidus and liquidus curve. Then the portion of the lever opposite to the phase whose amount is to be calculated is considered in the formula used as:

  $\text{Phase wt\%}=\frac{\text{opposite arm of lever}}{\text{total length of the tie line}}\times 100$ ..... (1)

Answer to Problem 10.80P

Both solid, as well as liquid phases, are present at the given conditions.

Composition of the liquid phase present is $72\text{ wt\% W}$.

Composition of the solid phase present is $91\text{ wt\% W}$.

Amount of the liquid phase is $57.89\%$.

Amount of the solid phase is $42.11\%$.

Explanation of Solution

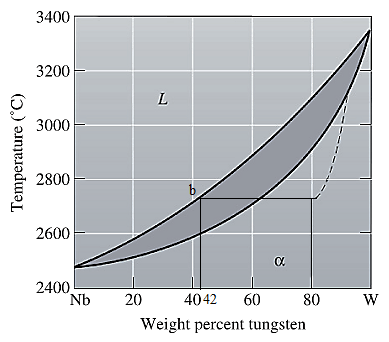
The equilibrium phase diagram for the Nb-W system is shown below as:

Now, draw a straight line from $\text{Nb-80 wt\% W}$ alloy composition at ${3000}^{\circ }\text{C}$ as shown below:

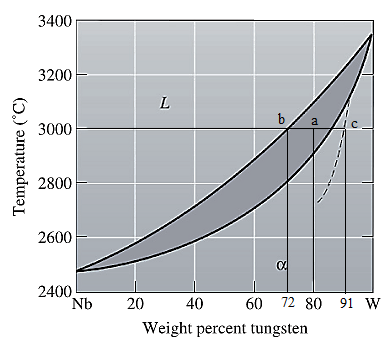
Both the phases, solid and liquid are present at this condition. Point 'b' represents the liquid phase composition in wt% and point 'c' represents the solid phase composition in wt% on the dashed curve. From the above phase diagram:

  $\begin{array}{c}L=72\text{ wt\% W}\\ S=91\text{ wt\% W}\end{array}$

To calculate the amount of liquid phase, lever 'ac' will be used and to calculate the amount of solid phase, lever 'ba' will be used. Use equation (1) to calculate the amount of each phase as:

  $\begin{array}{c}\text{Liquid wt\%}=\frac{\text{length of 'ac'}}{\text{length of 'bc'}}\times 100\\ =\frac{91-80}{91-72}\times 100\\ =57.89\text{ wt}\%\\ \text{Solid wt\%}=\frac{\text{length of 'ba'}}{\text{length of 'bc'}}\times 100\\ =\frac{80-72}{91-72}\times 100\\ =42.11\text{ wt}\%\end{array}$

Interpretation Introduction

(g)

Interpretation:

The phases present, their compositions and their amounts for $\text{Nb-80 wt\% W}$ alloy at ${2800}^{\circ }\text{C}$ are to be determined.

Concept Introduction:

On the temperature-composition graph of an alloy, the curve above which the alloy exists in the liquid phase is the liquidus curve. The temperature at this curve is the maximum temperature at which the crystals in the alloy can coexist with its melt in the thermodynamic equilibrium.

Solidus curve is the locus of the temperature on the temperature composition graph of an alloy, beyond which the alloy is completely in a solid phase.

Between the solidus and liquidus curve, the alloy exits in a slurry form in which there is both crystals as well as alloy melt.

Solidus temperature is always less than or equal to the liquidus temperature.

Amount of each phase in wt% is calculated using lever rule. At a particular temperature and alloy composition, a tie line is drawn on the phase diagram of the alloy between the solidus and liquidus curve. Then the portion of the lever opposite to the phase whose amount is to be calculated is considered in the formula used as:

  $\text{Phase wt\%}=\frac{\text{opposite arm of lever}}{\text{total length of the tie line}}\times 100$ ..... (1)

Answer to Problem 10.80P

Both solid, as well as liquid phases, are present at the given conditions.

Composition of the liquid phase present is $\text{51 wt\% W}$.

Composition of the solid phase present is $86\text{ wt\% W}$.

Amount of the liquid phase is $17.14\%$.

Amount of the solid phase is $82.86\%$.

Explanation of Solution

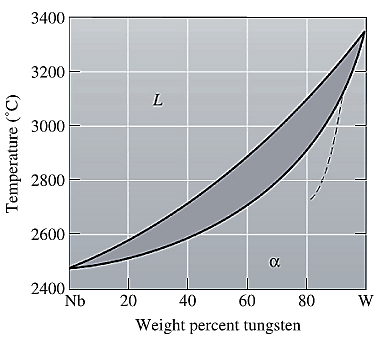
The equilibrium phase diagram for the Nb-W system is shown below as:

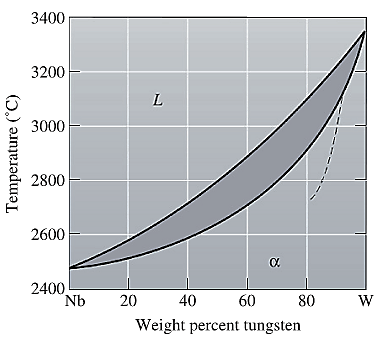
Now, draw a straight line from $\text{Nb-80 wt\% W}$ alloy composition at ${2800}^{\circ }\text{C}$ as shown below:

Both the phases, solid and liquid are present at this non-equilibrium condition. Point 'b' represents the liquid phase composition in wt% and point 'c' represents the solid phase composition in wt% at non-equilibrium conditions. From the above phase diagram:

  $\begin{array}{c}L=86\text{ wt\% W}\\ S=51\text{ wt\% W}\end{array}$

To calculate the amount of liquid phase, lever 'ac' will be used and to calculate the amount of solid phase, lever 'ba' will be used. Use equation (1) to calculate the amount of each phase as:

  $\begin{array}{c}\text{Liquid wt\%}=\frac{\text{length of 'ac'}}{\text{length of 'bc'}}\times 100\\ =\frac{86-80}{86-51}\times 100\\ =17.14\text{ wt}\%\\ \text{Solid wt\%}=\frac{\text{length of 'ba'}}{\text{length of 'bc'}}\times 100\\ =\frac{80-51}{86-51}\times 100\\ =82.86\text{ wt}\%\end{array}$