Chapter 10, Problem 10.44P

Interpretation Introduction

(a)

Interpretation:

The liquidus temperature, solidus temperature, and freezing range for NiO- $30\text{ mol\%}$ MgO ceramic composition are to be determined.

Concept Introduction:

On the temperature-composition graph of an alloy, the curve above which the alloy exist in the liquid phase is the liquidus curve. The temperature at this curve is maximum known as liquidus temperature at which the crystals in the alloy can coexist with its melt in the thermodynamic equilibrium.

Solidus curve is the locus of the temperature on the temperature composition graph of an alloy, beyond which the alloy is completely in solid phase. The temperature at this curve is minimum known as solidus temperature at which the crystals in the alloy can coexist with its melt in the thermodynamic equilibrium.

Freezing range for an alloy is the difference of the liquidus and the solidus temperature of an alloy. In this range, the alloy melt starts to crystallize at liquidus temperature and solidifies when reaches solidus temperature.

Answer to Problem 10.44P

Liquidus temperature, $T_L={2350}^{\circ }\text{C}$

Solidus temperature, $T_S={2160}^{\circ }\text{C}$

Freezing range, $\text{FR}={190}^{\circ }\text{C}$

Explanation of Solution

The equilibrium phase diagram for the NiO-MgO system is shown below as:

For NiO- $30\text{ mol\%}$ MgO, the straight line from $30\text{ mol\%}$ is drawn as shown. Liquidus temperature $\left(T_L\right)$ is represented by point 'a' where the line touches the upper curve. Solidus temperature $\left(T_S\right)$ is represented by point 'b' where the line touches the lower curve.

  $\begin{array}{c}{T}_L={2350}^{\circ }\text{C}\\ T_S={2160}^{\circ }\text{C}\end{array}$

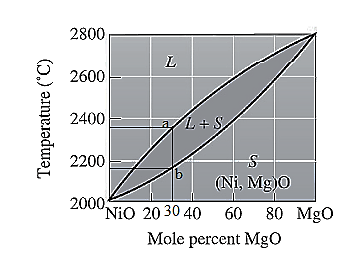
The freezing range (FR) for this ceramic composition will be:

  $\begin{array}{c}\text{FR}=T_L-T_S\\ =2350-2160\\ ={190}^{\circ }\text{C}\end{array}$

Interpretation Introduction

(b)

Interpretation:

The liquidus temperature, solidus temperature, and freezing range for NiO- $45\text{ mol\%}$ MgO ceramic composition are to be determined.

Concept Introduction:

On the temperature-composition graph of an alloy, the curve above which the alloy exist in the liquid phase is the liquidus curve. The temperature at this curve is maximum known as liquidus temperature at which the crystals in the alloy can coexist with its melt in the thermodynamic equilibrium.

Solidus curve is the locus of the temperature on the temperature composition graph of an alloy, beyond which the alloy is completely in solid phase. The temperature at this curve is minimum known as solidus temperature at which the crystals in the alloy can coexist with its melt in the thermodynamic equilibrium.

Freezing range for an alloy is the difference of the liquidus and the solidus temperature of an alloy. In this range, the alloy melt starts to crystallize at liquidus temperature and solidifies when reaches solidus temperature.

Answer to Problem 10.44P

Liquidus temperature, $T_L={2460}^{\circ }\text{C}$

Solidus temperature, $T_S={2250}^{\circ }\text{C}$

Freezing range, $\text{FR}={210}^{\circ }\text{C}$

Explanation of Solution

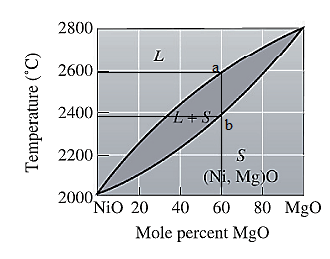
The equilibrium phase diagram for the NiO-MgO system is shown below as:

For NiO- $45\text{ mol\%}$ MgO, the straight line from $45\text{ mol\%}$ is drawn as shown. Liquidus temperature $\left(T_L\right)$ is represented by point 'a' where the line touches the upper curve. Solidus temperature $\left(T_S\right)$ is represented by point 'b' where the line touches the lower curve.

  $\begin{array}{c}{T}_L={2460}^{\circ }\text{C}\\ T_S={2250}^{\circ }\text{C}\end{array}$

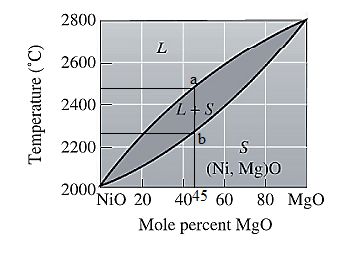
The freezing range (FR) for this ceramic composition will be:

  $\begin{array}{c}\text{FR}=T_L-T_S\\ =2460-2250\\ ={210}^{\circ }\text{C}\end{array}$

Interpretation Introduction

(c)

Interpretation:

The liquidus temperature, solidus temperature, and freezing range for NiO- $60\text{ mol\%}$ MgO ceramic composition are to be determined.

Concept Introduction:

On the temperature-composition graph of an alloy, the curve above which the alloy exist in the liquid phase is the liquidus curve. The temperature at this curve is maximum known as liquidus temperature at which the crystals in the alloy can coexist with its melt in the thermodynamic equilibrium.

Solidus curve is the locus of the temperature on the temperature composition graph of an alloy, beyond which the alloy is completely in solid phase. The temperature at this curve is minimum known as solidus temperature at which the crystals in the alloy can coexist with its melt in the thermodynamic equilibrium.

Freezing range for an alloy is the difference of the liquidus and the solidus temperature of an alloy. In this range, the alloy melt starts to crystallize at liquidus temperature and solidifies when reaches solidus temperature.

Answer to Problem 10.44P

Liquidus temperature, $T_L={2590}^{\circ }\text{C}$

Solidus temperature, $T_S={2380}^{\circ }\text{C}$

Freezing range, $\text{FR}={210}^{\circ }\text{C}$

Explanation of Solution

The equilibrium phase diagram for the NiO-MgO system is shown below as:

For NiO- $60\text{ mol\%}$ MgO, the straight line from $60\text{ mol\%}$ is drawn as shown. Liquidus temperature $\left(T_L\right)$ is represented by point 'a' where the line touches the upper curve. Solidus temperature $\left(T_S\right)$ is represented by point 'b' where the line touches the lower curve.

  $\begin{array}{c}{T}_L={2590}^{\circ }\text{C}\\ T_S={2380}^{\circ }\text{C}\end{array}$

The freezing range (FR) for this ceramic composition will be:

  $\begin{array}{c}\text{FR}=T_L-T_S\\ =2590-2380\\ ={210}^{\circ }\text{C}\end{array}$

Interpretation Introduction

(d)

Interpretation:

The liquidus temperature, solidus temperature, and freezing range for NiO- $85\text{ mol\%}$ MgO ceramic composition are to be determined.

Concept Introduction:

On the temperature-composition graph of an alloy, the curve above which the alloy exist in the liquid phase is the liquidus curve. The temperature at this curve is maximum known as liquidus temperature at which the crystals in the alloy can coexist with its melt in the thermodynamic equilibrium.

Solidus curve is the locus of the temperature on the temperature composition graph of an alloy, beyond which the alloy is completely in solid phase. The temperature at this curve is minimum known as solidus temperature at which the crystals in the alloy can coexist with its melt in the thermodynamic equilibrium.

Freezing range for an alloy is the difference of the liquidus and the solidus temperature of an alloy. In this range, the alloy melt starts to crystallize at liquidus temperature and solidifies when reaches solidus temperature.

Answer to Problem 10.44P

Liquidus temperature, $T_L={2740}^{\circ }\text{C}$

Solidus temperature, $T_S={2620}^{\circ }\text{C}$

Freezing range, $\text{FR}={120}^{\circ }\text{C}$

Explanation of Solution

The equilibrium phase diagram for the NiO-MgO system is shown below as:

For NiO- $85\text{ mol\%}$ MgO, the straight line from $85\text{ mol\%}$ is drawn as shown. Liquidus temperature $\left(T_L\right)$ is represented by point 'a' where the line touches the upper curve. Solidus temperature $\left(T_S\right)$ is represented by point 'b' where the line touches the lower curve.

  $\begin{array}{c}{T}_L={2740}^{\circ }\text{C}\\ T_S={2620}^{\circ }\text{C}\end{array}$

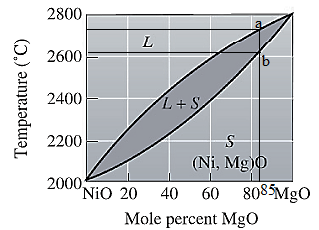
The freezing range (FR) for this ceramic composition will be:

  $\begin{array}{c}\text{FR}=T_L-T_S\\ =2740-2620\\ ={120}^{\circ }\text{C}\end{array}$