
Concept explainers
(a)
Graph
(a)
Answer to Problem 38PPS
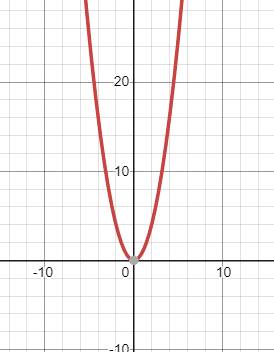
Explanation of Solution
Given:
The equation,
Concept Used:
The solutions of a
In order find the solutions of the given equation
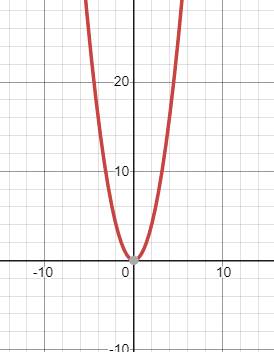
(b)
The vertex and two other points on the graph
(b)
Answer to Problem 38PPS
Vertex
Points
Explanation of Solution
Given:
In order find the vertex and two other points on the graph
Vertex points
(c)
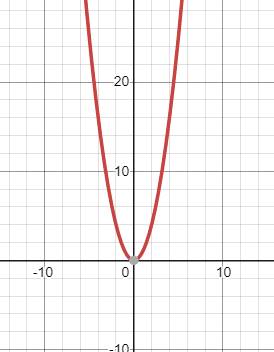
Graph
(c)
Answer to Problem 38PPS
Explanation of Solution
Given:
The equation,
Concept Used:
The solutions of a quadratic equation are given by the points where the graph of the function intersects the x-axis.
In order find the solutions of the given equation
The zeros of the function are the points where the graph of the function intersects the x-axis.
The graph of the function
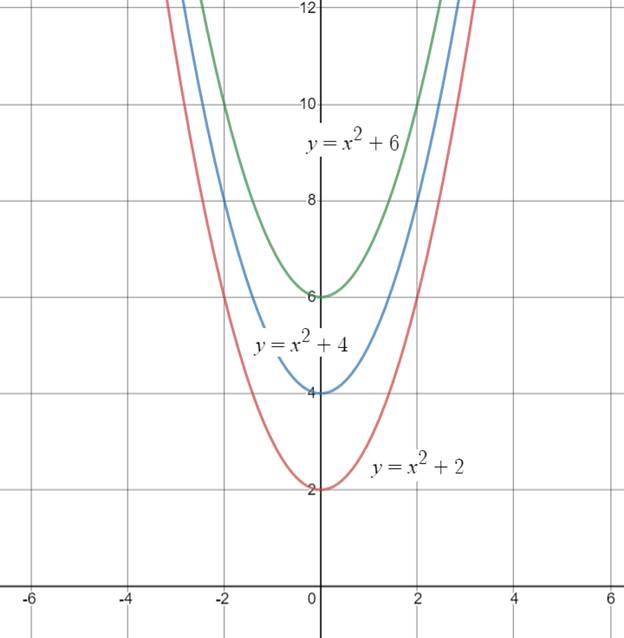
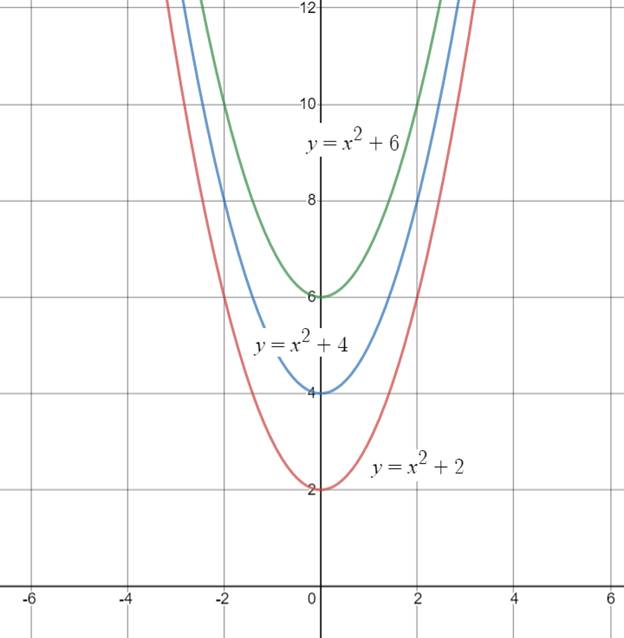
(d)
The vertex and two points from each of these graphs that have the same x-coordinates
(d)
Answer to Problem 38PPS
The equation is
Explanation of Solution
Given:
The equation
Concept Used:
The solutions of a quadratic equation are given by the points where the graph of the function intersects the x-axis.
In order find the vertex and two points from each of these graphs that have the same x-coordinates the solutions of a quadratic equation are given by the points where the graph of the function intersects the x-axis. The equation is
(e)
The conclusion
(e)
Answer to Problem 38PPS
The equation is
Explanation of Solution
The equation is
(e)
The conclusion
(e)
Answer to Problem 38PPS
The equation is
Explanation of Solution
The equation is
Chapter 9 Solutions
Glencoe Algebra 1, Student Edition, 9780079039897, 0079039898, 2018
Additional Math Textbook Solutions
Algebra and Trigonometry (6th Edition)
Thinking Mathematically (6th Edition)
Elementary Statistics (13th Edition)
Intro Stats, Books a la Carte Edition (5th Edition)
Elementary Statistics: Picturing the World (7th Edition)
Calculus: Early Transcendentals (2nd Edition)
- most 2, and let Let P2 denote the vector space of polynomials of degree at D: P2➡ P2 be the transformation that sends a polynomial p(t) = at² + bt+c in P2 to its derivative p'(t) 2at+b, that is, D(p) = p'. (a) Prove that D is a linear transformation. (b) Find a basis for the kernel ker(D) of the linear transformation D and compute its nullity. (c) Find a basis for the image im(D) of the linear transformation D and compute its rank. (d) Verify that the Rank-Nullity Theorem holds for the linear transformation D. (e) Find the matrix representation of D in the standard basis (1,t, t2) of P2.arrow_forward(c) Let A = -1 3 -4 12 3 3 -9 (i) Find bases for row(A), col(A) and N(A). (ii) Determine the rank and nullity of A, and verify that the Rank-Nullity Theorem holds for the above matrix A.arrow_forward-(0)-(0)-(0) X1 = x2 = x3 = 1 (a) Show that the vectors X1, X2, X3 form a basis for R³. y= (b) Find the coordinate vector [y] B of y in the basis B = (x1, x2, x3).arrow_forward
- Let A 1 - 13 (1³ ³) 3). (i) Compute A2, A3, A4. (ii) Show that A is invertible and find A-¹.arrow_forwardLet H = {(a a12 a21 a22, | a1 + a2 = 0} . € R²x²: a11 + a22 (i) Show that H is a subspace of R2×2 (ii) Find a basis of H and determine dim H.arrow_forward2 5 A=1 2 -2 b=2 3 1 -1 3 (a) Calculate det(A). (b) Using (a), deduce that the system Ax = b where x = (x1, x2, x3) is consistent and determine x2 using Cramer's rule.arrow_forward
- Consider the least squares problem Ax = b, where 12 -09-0 A 1 3 1 4 and b = (a) Write down the corresponding normal equations. (b) Determine the set of least squares solutions to the problem.arrow_forwardThe function f(x) is represented by the equation, f(x) = x³ + 8x² + x − 42. Part A: Does f(x) have zeros located at -7, 2, -3? Explain without using technology and show all work. Part B: Describe the end behavior of f(x) without using technology.arrow_forwardHow does the graph of f(x) = (x − 9)4 – 3 compare to the parent function g(x) = x²?arrow_forward
- Find the x-intercepts and the y-intercept of the graph of f(x) = (x − 5)(x − 2)(x − 1) without using technology. Show all work.arrow_forwardIn a volatile housing market, the overall value of a home can be modeled by V(x) = 415x² - 4600x + 200000, where V represents the value of the home and x represents each year after 2020. Part A: Find the vertex of V(x). Show all work. Part B: Interpret what the vertex means in terms of the value of the home.arrow_forwardShow all work to solve 3x² + 5x - 2 = 0.arrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





