
Concept explainers
a.
The expression to represent the amount of money saved after w weeks.
a.
Answer to Problem 19IP
Explanation of Solution
Given:
She is saving money to buy an MP3 player that costs $212. She already saved $47 and plans to save an additional $15 per week.
Calculation:
In order to write an expression to represent the amount of money saved after w weeks, observe that she already have save $47, so it is the fixed amount and she plans to save an additional $15 every week, so an expression to represent the situation could be
Thus, the expression to represent the amount of money saved after w weeks is
So, the table can be filled using this expression as
| Number of weeks | Amount of saving ($) |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
b.
The line graph of the data in the table.
b.
Explanation of Solution
Given:
She is saving money to buy an MP3 player that costs $212. She already saved $47 and plans to save an additional $15 per week.
Calculation:
The plot of the data points from the table is shown below,
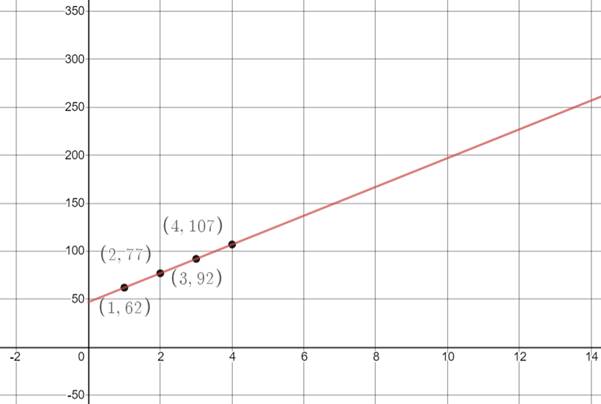
From the graph it is clear that she will have enough money for the MP3 player after 11th week.
c.
The number of weeks it will take her to save the money.
c.
Answer to Problem 19IP
Explanation of Solution
Given:
She is saving money to buy an MP3 player that costs $212. She already saved $47 and plans to save an additional $15 per week.
Calculation:
In order to write an expression to represent the amount of money saved after w weeks, observe that she already have save $47, so it is the fixed amount and she plans to save an additional $15 every week, so an expression to represent the situation could be
Since the cost of the MP3 player is $212, so substitute this value of A in above equation and solve for w as shown below,
So, it will take her 11 weeks to save the money to buy MP3.
d.
To compare the methods for finding the solution used in part (b) and (c).
d.
Explanation of Solution
Given:
She is saving money to buy an MP3 player that costs $212. She already saved $47 and plans to save an additional $15 per week.
Calculation:
Using the graph, once can estimate the time when she can have enough money to buy the MP3, while using the equation, one can find the exact time when she will have the required amount of money.
Chapter 8 Solutions
Glencoe Math Accelerated, Student Edition
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Intro Stats, Books a la Carte Edition (5th Edition)
Calculus: Early Transcendentals (2nd Edition)
Calculus: Early Transcendentals (2nd Edition)
Elementary Statistics: Picturing the World (7th Edition)
- please do Q3arrow_forwardUse the properties of logarithms, given that In(2) = 0.6931 and In(3) = 1.0986, to approximate the logarithm. Use a calculator to confirm your approximations. (Round your answers to four decimal places.) (a) In(0.75) (b) In(24) (c) In(18) 1 (d) In ≈ 2 72arrow_forwardFind the indefinite integral. (Remember the constant of integration.) √tan(8x) tan(8x) sec²(8x) dxarrow_forward
- Find the indefinite integral by making a change of variables. (Remember the constant of integration.) √(x+4) 4)√6-x dxarrow_forwarda -> f(x) = f(x) = [x] show that whether f is continuous function or not(by using theorem) Muslim_mathsarrow_forwardUse Green's Theorem to evaluate F. dr, where F = (√+4y, 2x + √√) and C consists of the arc of the curve y = 4x - x² from (0,0) to (4,0) and the line segment from (4,0) to (0,0).arrow_forward
- Evaluate F. dr where F(x, y, z) = (2yz cos(xyz), 2xzcos(xyz), 2xy cos(xyz)) and C is the line π 1 1 segment starting at the point (8, ' and ending at the point (3, 2 3'6arrow_forwardCan you help me find the result of an integral + a 炉[メをメ +炉なarrow_forward2 a Can you help me find the result of an integral a 아 x² dxarrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





