Chapter 8, Problem 8.8.3P

To determine

(a)

The design of a four-bolt unstiffened end-plate connection for a $W18\times 40$ beam to a $W8\times 40$ column for the full moment and shear capacities of the beam by using LRFD.

Answer to Problem 8.8.3P

$PL1\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.\times 7\times 2^{\text{'}}-1{\frac{1}{8}}^{\text{'}\text{'}}$and four $1\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$-in. diameter Group A fully tightened bolts at each flange

9/16-in. fillet weld at each flange.

¼-in. fillet weld on each side of the web in the tension region.

½-in. fillet weld on each side of the web between mid-depth and the compression flange.

Explanation of Solution

Given:

A992 steel for members

A36 steel for the end plate

Group A pretensioned bolts

Formula used:

$P_t=F_t{A}_b$

$P_t$ is bolt strength

$F_t$ is the ultimate tensile stress of the bolt

$A_b$ is the bolt area

$M_n=2P_t\left(h_0+h_1\right)$

$M_n$ is required moment strength

$h_0$ is distance from center of beam compression flange to center ofouter row of bolts on the tension side.

$h_1$ is distance from center of compression flange to center of inner rowof bolts.

$t_p=\sqrt{\frac{1.11\varphi M_n}{{\varphi }_b{F}_y{Y}_p}}$

$t_p$ isend plate thickness

$Y_p$ is yield line mechanism parameter

${\varphi }_b=0.90$

Calculation:

From the $Z_x$ tables, for a $W18\times 40$,

$\begin{array}{l}{M}_u={\varphi }_b{M}_{px}=294ft-kips\\ V_u={\varphi }_v{V}_n=169kips\end{array}$

From the dimensions and properties tables

$\begin{array}{l}d=17.9in.\\ t_w=0.315in.\\ b_{fb}=6.02in.\\ t_{fb}=0.525in.\end{array}$

Workable gauge = 3.50 in.

For the bolt pitch, try $p_{fo}=p_{fi}=2in.$

For the gauge distance, use the workable gauge g = 3.50 in.

Required bolt diameter:

$\begin{array}{l}{h}_0=d-\frac{t_{fb}}{2}+p_{fo}=17.9-\frac{0.525}{2}+2=19.64in.\\ h_1=d-\frac{t_{fb}}{2}-t_{fb}-p_{fi}=17.9-\frac{0.525}{2}-0.525-2=15.11in.\\ d_{b\mathrm{Re}quired}=\sqrt{\frac{2M_u}{\pi \varphi F_t\left(h_0+h_1\right)}}=\sqrt{\frac{2\left(294\times 12\right)}{\pi \left(0.75\right)\left(90\right)\left(19.64+15.11\right)}}=0.979in.\end{array}$

Try $d_b=1in.$

Moment strength based on bolt strength:

$\begin{array}{l}{P}_t=F_t{A}_b=90\left(\frac{\pi {\left(1\right)}^2}{4}\right)=70.69kips/bolt\\ M_n=2P_t\left(h_0+h_1\right)=2\left(70.69\right)\left(19.64+15.11\right)=4913in.-kips\\ \varphi M_n=0.75\left(4913\right)=3685in.-kips=307.1ft-kips>{\varphi }_b{M}_{px}=294ft-kips\end{array}$

Therefore, use $\varphi M_n={\varphi }_b{M}_{px}=294ft-kips=3528in.-kips$

Determine end-plate width:

Minimum $l_e=1\frac{1}{4}in.$

The minimum plate width is $g+2l_e=3.50+2\left(1.25\right)=6in.$ but no less than the beam flange width of 6.02in.

Maximum effective end-plate width = $b_{fb}+1=6.02+1=7.02in.$

Try $b_p=7in.$

Determine the required plate thickness:

$\begin{array}{l}s=\frac{1}{2}\sqrt{b_{p}g}=\frac{1}{2}\sqrt{7\left(3.5\right)}\\ =2.457in.>p_{fi}\end{array}$

Therefore, use the original value of $p_{fi}=2in.$

$\begin{array}{l}{Y}_p=\frac{b_p}{2}\left[h_1\left(\frac{1}{p_{fi}}+\frac{1}{s}\right)+h_0\left(\frac{1}{p_{fo}}\right)-\frac{1}{2}\right]+\frac{2}{g}\left[h_1\left(p_{fi}+s\right)\right]\\ =\frac{7}{2}\left[15.11\left(\frac{1}{2}+\frac{1}{2.475}\right)+19.64\left(\frac{1}{2}\right)-\frac{1}{2}\right]+\frac{2}{3.5}\left[15.11\left(2+2.475\right)\right]\\ =119.1\end{array}$

Required $t_p=\sqrt{\frac{1.11\varphi M_n}{{\varphi }_b{F}_y{Y}_p}}=\sqrt{\frac{1.11\left(3528\right)}{0.9\left(36\right)\left(119.1\right)}}=1.01in.$

Try $t_p=1\frac{1}{4}in.$

Beam flange force:

$\begin{array}{l}{F}_{f_u}=\frac{M_u}{d-t_{fb}}=\frac{294\times 12}{17.9-0.525}=203.1kips\\ \frac{F_{f_u}}{2}=\frac{203.1}{2}=101.6kips\end{array}$

The shear yield strength of the end plate is

$\varphi \left(0.6\right)F_y{t}_p{b}_p=0.90\left(0.6\right)\left(36\right)\left(1.25\right)\left(7\right)=170.1kips>101.6kips$ (OK)

Shear rupture strength of end plate:

$A_n=t_p\left[b_p-2\left(d_b+\frac{1}{8}\right)\right]=1.25\left[7-2\left(1+\frac{1}{8}\right)\right]=5.938in{.}^2$

$\varphi \left(0.6\right)F_u{A}_n=0.75\left(0.6\right)\left(58\right)\left(5.938\right)=155kips>101.6kips$ (Ok)

Check bolt shear:

The compression side bolts must be capable of resisting the entire vertical shear.

$\begin{array}{l}{A}_b=\frac{\pi d_b^2}{4}=\frac{\pi {\left(1\right)}^2}{4}=0.785in{.}^2\\ \varphi R_n=\varphi F_{nv}{A}_b=0.75\left(54\right)\left(0.7854\right)=31.81kips/bolt\end{array}$

For 4 bolts,

$\varphi R_n=4\times 31.81=127.2kips$

$V_u=169kips>127.2kips$ (N.G.)

Try $1\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.in.$

$\begin{array}{l}{A}_b=\frac{\pi d_b^2}{4}=\frac{\pi {\left(1.25\right)}^2}{4}=1.227in{.}^2\\ \varphi R_n=\varphi F_{nv}{A}_b=0.75\left(54\right)\left(1.227\right)=49.69kips/bolt\end{array}$

For 4 bolts, $\varphi R_n=4\times 49.69=199kips>169kips$ (OK)

Recompute the plate dimensions:

For $1\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.in.$ diameter bolts,

Minimum $l_e=1\frac{5}{8}in.$

The minimum plate width is

$g+2l_e=3.50+2\left(1.625\right)=6.75in.$

Maximum effective end-plate width = $b_{fb}+1=6.02+1=7.02in.$

Use the currently selected width of $b_p=7in.$

Because the bolt size has increased, check the shear rupture strength of the end plate:

$A_n=t_p\left[b_p-2\left(d_b+\frac{1}{8}\right)\right]=1.25\left[7-2\left(1.25+\frac{1}{8}\right)\right]=5.313in{.}^2$

$\varphi \left(0.6\right)F_u{A}_n=0.75\left(0.6\right)\left(58\right)\left(5.313\right)=138.7kips>101.6kips$ (OK)

Check bearing in the plate at the compression side bolts.

$h=d+\frac{1}{16}=1\frac{1}{4}+\frac{1}{16}=1.313in.$

For the outer bolts,

$\begin{array}{l}{l}_c=p_{fo}+t_{fb}+p_{fi}-h=2+0.525+2-1.313=3.212in.\\ \varphi R_n=\varphi \left(1.2l_{c}t{F}_u\right)=0.75\left(1.2\right)\left(3.212\right)\left(1.25\right)\left(58\right)=209.6kips\end{array}$

The upper limit is

$\varphi \left(2.4dt{F}_u\right)=0.75\left(2.4\right)\left(1.25\right)\left(1.25\right)\left(58\right)=163.1kips<209.6kips$

Therefore, use $\varphi R_n=163.1kips/bolt$

Since the inner bolts are not near an edge or adjacent bolts, the outer bolts control.

The total bearing strength is

$4\times 163.1=652kips>V_u=169kips$ (Ok)

Check bearing in the column flange:

Use $l_c=3.212in.$

$\varphi R_n=\varphi \left(1.2l_{c}t{F}_u\right)=0.75\left(1.2\right)\left(3.212\right)\left(0.525\right)\left(65\right)=98.65kips$

The upper limit is

$\varphi \left(2.4dt{F}_u\right)=0.75\left(2.4\right)\left(1.25\right)\left(0.525\right)\left(65\right)=76.78kips<98.65kips$

Therefore, use $\varphi R_n=76.78kips/bolt$

The total bearing strength is

$4\times 76.78=307kips>V_u=169kips$ (OK)

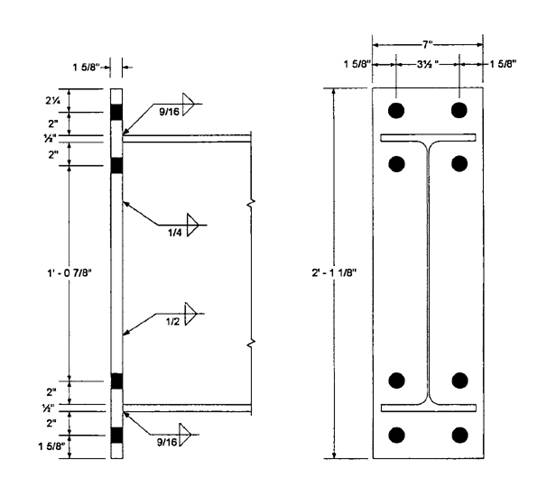
The plate length, using detailing dimensions and the notation of figure given below from the textbook (Steel design), is

$d+2p_{fo}+2d_e=17\frac{7}{8}+2\left(2\right)+2\left(1\frac{5}{8}\right)=25\frac{1}{8}in.$

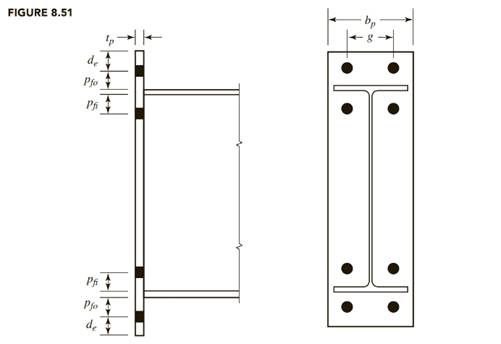
Use a $PL1\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.\times 7\times 2^{\text{'}}-1{\frac{1}{8}}^{\text{'}\text{'}}$ and four $1\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$ -in. diameter Group A fully-tightened bolts at each flange.

Beam flange to plate weld design:

The flange force is

$F_{fu}=203.1kips$

AISC Design Guide 4 recommends that the minimum design flange force should be 60% of the flange yield strength:

Minimum $F_{fu}=0.6F_y\left(b_{fb}{t}_{fb}\right)=0.6\left(50\right)\left(6.02\right)\left(.525\right)=94.8kips<203.1kips$

Therefore, use the actual flange force of 203.1 kips.

The flange weld length is

$b_{fb}+\left(b_{fb}-t_w\right)=6.02+\left(6.02-0.315\right)=11.73in.$

The weld strength is

$\varphi R_n=1.392D\times 11.73\times 1.5$

where D is the weld size in sixteenths of an inch and the factor of 1.5 accounts for the direction of the load on the weld. If we equate the weld strength to the flange force,

$1.392D\times 11.73\times 1.5=203.1$

$D=8.29$ sixteenths

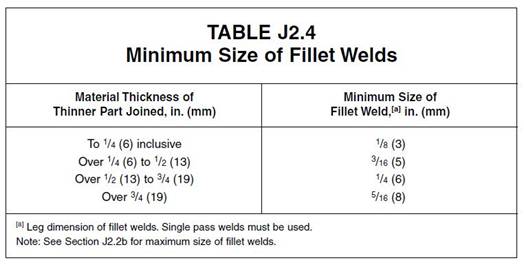
From AISC Table J2.4, the minimum weld size is ¼-in. (based on the thickness of the flange, which is the thinner connected part).

Use a 9/16-in. fillet weld at each flange.

Beam web to plate weld design:

To develop the yield stress in the web near the tension bolts, let

$1.392D\times 2=0.6F_y{t}_w$ for two welds, one on each side of the web. The required weld size is

$D=\frac{0.6F_y{t}_w}{1.392\left(2\right)}=\frac{0.6\left(50\right)\left(0.315\right)}{1.392\left(2\right)}=3.39$ sixteenths

Use a ¼-in. fillet weld on each side of the web in the tension region.

The applied shear of $V_u=169kips$ must be resisted by welding a length of web equal to the smaller of the following two lengths:

1. From the mid-depth to the compression flange.

$L=\frac{d}{2}-t_{fb}=\frac{17.9}{2}-0.525=8.425in.$

From the inner row of tension bolts plus $2d_b$

1. to the compression flange:

$L=d-2t_{fb}-p_{fi}-2d_b=17.9-2\left(0.525\right)-2.0-2\left(1.25\right)=12.35in.>8.425in.$

Equating the weld strength to the required shear strengths, we get

$1.392D\times 8.425\times 2=169$

$D=7.21$ sixteenths ( $w=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.in.$ )

From AISC Table J2.4, the minimum weld size is 3/16-in.

Use a ½-in. fillet weld on each side of the web between mid-depth and the compression flange.

The design is summarized in the figure below:

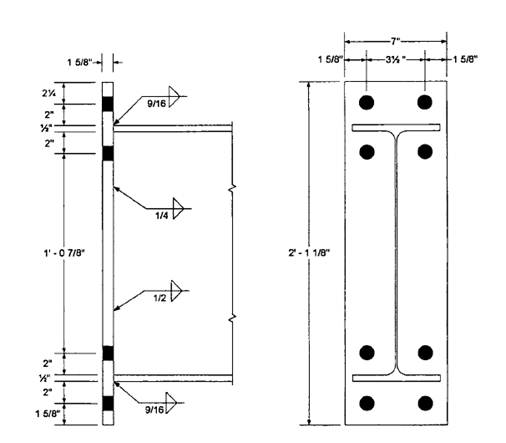
Conclusion:

Use a $PL1\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.\times 7\times 2^{\text{'}}-1{\frac{1}{8}}^{\text{'}\text{'}}$ and four $1\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$ -in. diameter Group A fully-tightened bolts at each flange, a 9/16-in. fillet weld at each flange, a ¼-in. fillet weld on each side of the web in the tension region and a ½-in. fillet weld on each side of the web between mid-depth and the compression flange.

To determine

(b)

The design of a four-bolt unstiffened end-plate connection for a $W18\times 40$ beam to a $W8\times 40$ column for the full moment and shear capacities of the beam by using ASD.

Answer to Problem 8.8.3P

$PL1\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.\times 7\times 2^{\text{'}}-1{\frac{1}{8}}^{\text{'}\text{'}}$and four $1\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$-in. diameter Group A fully tightened bolts at each flange

9/16-in. fillet weld at each flange.

¼-in. fillet weld on each side of the web in the tension region

½-in. fillet weld on each side of the web between mid-depth and the compression flange.

Explanation of Solution

Given:

A992 steel for members

A36 steel for the end plate

Group A pretensioned bolts

Formula used:

$P_t=F_t{A}_b$

$P_t$ is bolt strength

$F_t$ is the ultimate tensile stress of the bolt

$A_b$ is the bolt area

$M_n=2P_t\left(h_0+h_1\right)$

$M_n$ is required moment strength

$h_0$ is distance from center of beam compression flange to center ofouter row of bolts on the tension side

$h_1$ is distance from center of compression flange to center of inner rowof bolts

$t_p=\sqrt{\frac{1.11\left(M_n/\Omega \right)}{F_y{Y}_p/{\Omega }_b}}$

$t_p$ is end plate thickness

$Y_p$ is yield line mechanism parameter

${\Omega }_b=1.67$

Calculation:

From the $Z_x$ tables, for a $W18\times 40$,

$\begin{array}{l}{M}_a=\frac{M_{px}}{{\Omega }_b}=196ft-kips\\ V_a=\frac{V_{nx}}{{\Omega }_v}=113kips\end{array}$

From the dimensions and properties tables

$\begin{array}{l}d=17.9in.\\ t_w=0.315in.\\ b_{fb}=6.02in.\\ t_{fb}=0.525in.\end{array}$

Workable gauge = 3.50 in.

For the bolt pitch, try $p_{fo}=p_{fi}=2in.$

For the gauge distance, use the workable gauge g = 3.50 in.

Required bolt diameter:

$\begin{array}{l}{h}_0=d-\frac{t_{fb}}{2}+p_{fo}=17.9-\frac{0.525}{2}+2=19.64in.\\ h_1=d-\frac{t_{fb}}{2}-t_{fb}-p_{fi}=17.9-\frac{0.525}{2}-0.525-2=15.11in.\\ d_{b\mathrm{Re}quired}=\sqrt{\frac{\Omega \left(2M_a\right)}{\pi F_t\left(h_0+h_1\right)}}=\sqrt{\frac{2.0\left(2\times 196\times 12\right)}{\pi \left(90\right)\left(19.64+15.11\right)}}=0.9785in.\end{array}$

Try $d_b=1in.$

Moment strength based on bolt strength:

$\begin{array}{l}{P}_t=F_t{A}_b=90\left(\frac{\pi {\left(1\right)}^2}{4}\right)=70.69kips/bolt\\ M_n=2P_t\left(h_0+h_1\right)=2\left(70.69\right)\left(19.64+15.11\right)=4913in.-kips\\ \frac{M_n}{\Omega }=\frac{4913}{2.0}=2456.5in.-kips=204.708ft-kips>\frac{M_{px}}{{\Omega }_b}=196ft-kips\end{array}$

Therefore, use $\frac{M_n}{\Omega }=\frac{M_{px}}{{\Omega }_b}=196ft-kips=2352in.-kips$

Determine end-plate width:

Minimum $l_e=1\frac{1}{4}in.$

The minimum plate width is $g+2l_e=3.50+2\left(1.25\right)=6in.$ but no less than the beam flange width of 6.02 in.

Maximum effective end-plate width = $b_{fb}+1=6.02+1=7.02in.$

Try $b_p=7in.$

Determine the required plate thickness:

$\begin{array}{l}s=\frac{1}{2}\sqrt{b_{p}g}=\frac{1}{2}\sqrt{7\left(3.5\right)}\\ =2.457in.>p_{fi}\end{array}$

Therefore, use the original value of $p_{fi}=2in.$

$\begin{array}{l}{Y}_p=\frac{b_p}{2}\left[h_1\left(\frac{1}{p_{fi}}+\frac{1}{s}\right)+h_0\left(\frac{1}{p_{fo}}\right)-\frac{1}{2}\right]+\frac{2}{g}\left[h_1\left(p_{fi}+s\right)\right]\\ =\frac{7}{2}\left[15.11\left(\frac{1}{2}+\frac{1}{2.475}\right)+19.64\left(\frac{1}{2}\right)-\frac{1}{2}\right]+\frac{2}{3.5}\left[15.11\left(2+2.475\right)\right]\\ =119.1\end{array}$

Required $t_p=\sqrt{\frac{1.11\left(M_n/\Omega \right)}{F_y{Y}_p/{\Omega }_b}}=\sqrt{\frac{1.11\left(2352\right)}{36\left(119.1\right)/1.67}}=1.0084in.$

Try $t_p=1\frac{1}{4}in.$

Beam flange force:

$\begin{array}{l}{F}_{f_u}=\frac{M_a}{d-t_{fb}}=\frac{196\times 12}{17.9-0.525}=135.4kips\\ \frac{F_{f_u}}{2}=\frac{135.4}{2}=67.68kips\end{array}$

The shear yield strength of the end plate is

$\frac{\left(0.6\right)F_y{t}_p{b}_p}{\Omega }=\frac{0.6\left(36\right)\left(1.25\right)\left(7\right)}{1.67}=113.17kips>67.68kips$ (OK)

Shear rupture strength of end plate:

$A_n=t_p\left[b_p-2\left(d_b+\frac{1}{8}\right)\right]=1.25\left[7-2\left(1+\frac{1}{8}\right)\right]=5.938in{.}^2$

$\frac{0.6F_u{A}_n}{\Omega }=\frac{0.6\left(58\right)\left(5.938\right)}{2.0}=103.32kips>67.68kips$ (Ok)

Check bolt shear:

The compression side bolts must be capable of resisting the entire vertical shear.

$\begin{array}{l}{A}_b=\frac{\pi d_b^2}{4}=\frac{\pi {\left(1\right)}^2}{4}=0.785in{.}^2\\ \frac{R_n}{\Omega }=\frac{F_{nv}{A}_b}{\Omega }=\frac{54\left(0.7854\right)}{2.0}=21.2kips/bolt\end{array}$

For 4 bolts,

$\frac{R_n}{\Omega }=4\times 21.2=84.8kips$

$V_a=113kips>84.8kips$ (N.G.)

Try $1\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.in.$

$\begin{array}{l}{A}_b=\frac{\pi d_b^2}{4}=\frac{\pi {\left(1.25\right)}^2}{4}=1.227in{.}^2\\ \frac{R_n}{\Omega }=\frac{F_{nv}{A}_b}{\Omega }=\frac{54\left(1.227\right)}{2.0}=33.129kips/bolt\end{array}$

For 4 bolts, $\varphi R_n=4\times 33.129=132.516kips>113kips$ (OK)

Recompute the plate dimensions:

For $1\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.in.$ diameter bolts,

Minimum $l_e=1\frac{5}{8}in.$

The minimum plate width is

$g+2l_e=3.50+2\left(1.625\right)=6.75in.$

Maximum effective end-plate width = $b_{fb}+1=6.02+1=7.02in.$

Use the currently selected width of $b_p=7in.$

Because the bolt size has increased, check the shear rupture strength of the end plate:

$A_n=t_p\left[b_p-2\left(d_b+\frac{1}{8}\right)\right]=1.25\left[7-2\left(1.25+\frac{1}{8}\right)\right]=5.313in{.}^2$

$\frac{0.6F_u{A}_n}{\Omega }=\frac{0.6\left(58\right)\left(5.313\right)}{2.0}=92.446kips>67.68kips$ (OK)

Check bearing in the plate at the compression side bolts.

$h=d+\frac{1}{16}=1\frac{1}{4}+\frac{1}{16}=1.313in.$

For the outer bolts,

$\begin{array}{l}{l}_c=p_{fo}+t_{fb}+p_{fi}-h=2+0.525+2-1.313=3.212in.\\ \frac{R_n}{\Omega }=\frac{1.2l_{c}t{F}_u}{\Omega }=\frac{1.2\left(3.212\right)\left(1.25\right)\left(58\right)}{2.0}=139.722kips\end{array}$

The upper limit is

$\frac{2.4dt{F}_u}{\Omega }=\frac{2.4\left(1.25\right)\left(1.25\right)\left(58\right)}{2.0}=108.75kips<139.722kips$

Therefore, use $\frac{R_n}{\Omega }=108.75kips/bolt$

Since the inner bolts are not near an edge or adjacent bolts, the outer bolts control.

The total bearing strength is

$4\times 108.75=435kips>V_a=113kips$ (Ok)

Check bearing in the column flange:

Use $l_c=3.212in.$

$\frac{R_n}{\Omega }=\frac{1.2l_{c}t{F}_u}{\Omega }=\frac{1.2\left(3.212\right)\left(0.525\right)\left(65\right)}{2.0}=65.766kips$

The upper limit is

$\frac{2.4dt{F}_u}{\Omega }=\frac{2.4\left(1.25\right)\left(0.525\right)\left(65\right)}{2.0}=51.1875kips<65.766kips$

Therefore, use $\frac{R_n}{\Omega }=51.1875kips/bolt$

The total bearing strength is

$4\times 51.1875=204.75kips>V_u=113kips$ (OK)

The plate length, using detailing dimensions and the notation of figure given below from the textbook, is

$d+2p_{fo}+2d_e=17\frac{7}{8}+2\left(2\right)+2\left(1\frac{5}{8}\right)=25\frac{1}{8}in.$

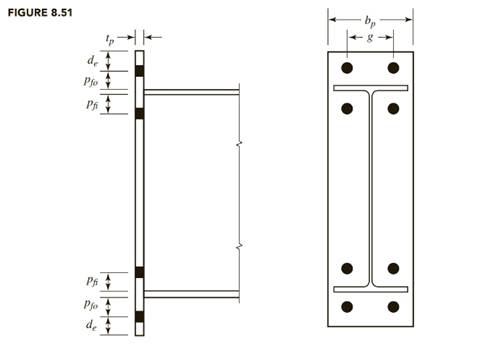
Use a $PL1\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.\times 7\times 2^{\text{'}}-1{\frac{1}{8}}^{\text{'}\text{'}}$ and four $1\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$ -in. diameter Group A fully-tightened bolts at each flange.

Beam flange to plate weld design:

The flange force is

$F_{fu}=135.4kips$

AISC Design Guide 4 recommends that the minimum design flange force should be 60% of the flange yield strength:

Minimum $F_{fu}=0.6F_y\left(b_{fb}{t}_{fb}\right)=0.6\left(50\right)\left(6.02\right)\left(.525\right)=94.8kips<135.4kips$

Therefore, use the actual flange force of 135.4 kips.

The flange weld length is

$b_{fb}+\left(b_{fb}-t_w\right)=6.02+\left(6.02-0.315\right)=11.73in.$

The weld strength is

$\frac{R_n}{\Omega }=1.392D\times 11.73\times 1.5$

where D is the weld size in sixteenths of an inch and the factor of 1.5 accounts for the direction of the load on the weld. If we equate the weld strength to the flange force,

$1.392D\times 11.73\times 1.5=135.4$

$D=5.53$ sixteenths

From AISC Table J2.4, the minimum weld size is ¼-in. (based on the thickness of the flange, which is the thinner connected part).

Use a 9/16-in. fillet weld at each flange.

Beam web to plate weld design:

To develop the yield stress in the web near the tension bolts, let

$1.392D\times 2=0.6F_y{t}_w$ for two welds, one on each side of the web. The required weld size is

$D=\frac{0.6F_y{t}_w}{1.392\left(2\right)}=\frac{0.6\left(50\right)\left(0.315\right)}{1.392\left(2\right)}=3.39$ sixteenths

Use a ¼-in. fillet weld on each side of the web in the tension region.

The applied shear of $V_a=113kips$ must be resisted by welding a length of web equal to the smaller of the following two lengths:

1. From the mid-depth to the compression flange.

$L=\frac{d}{2}-t_{fb}=\frac{17.9}{2}-0.525=8.425in.$

From the inner row of tension bolts plus $2d_b$

1. to the compression flange:

$L=d-2t_{fb}-p_{fi}-2d_b=17.9-2\left(0.525\right)-2.0-2\left(1.25\right)=12.35in.>8.425in.$

Equating the weld strength to the required shear strengths, we get

$1.392D\times 8.425\times 2=113$

$D=4.82$ sixteenths ( $w=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.in.$ )

From AISC Table J2.4, the minimum weld size is 3/16-in.

Use a ½-in. fillet weld on each side of the web between mid-depth and the compression flange.

The design is summarized in the figure below:

Conclusion:

Use a $PL1\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.\times 7\times 2^{\text{'}}-1{\frac{1}{8}}^{\text{'}\text{'}}$ and four $1\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$ -in. diameter Group A fully-tightened bolts at each flange, a 9/16-in. fillet weld at each flange, a ¼-in. fillet weld on each side of the web in the tension region and a ½-in. fillet weld on each side of the web between mid-depth and the compression flange.