Differential Equations: An Introduction to Modern Methods and Applications
3rd Edition
ISBN: 9781118531778
Author: James R. Brannan, William E. Boyce
Publisher: WILEY
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 7.5, Problem 14P
a) By examining the graphs of
b) Calculate and plot the graphs of solutions of the van der Pol equation for other values of the parameter
c) Plot the estimated values of
Expert Solution & Answer
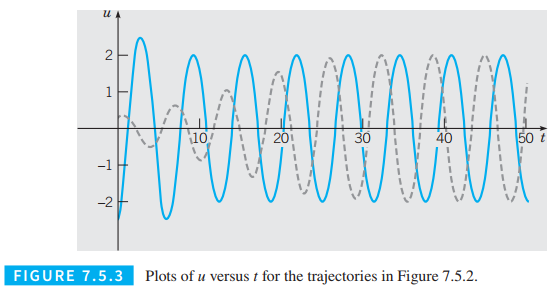
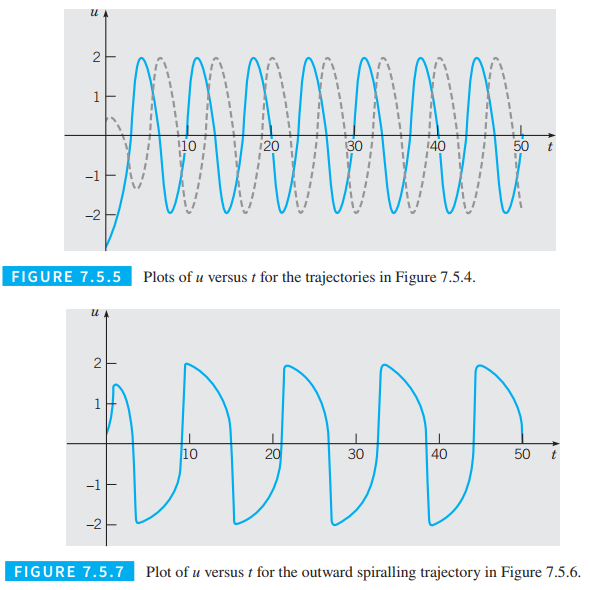
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
10. An airplane flying 390 feet per second at an altitude of 5000 feet flew directly over an observer. The
image shows the relationship of the airplane to the observer at a
later time.
a.) Find an equation relating x and y.
5000°t 390
5000
b.) Find the value of x when y is 6,250.
Observer
c.) How fast is the distance from the observer to the airplane changing at the time when the airplane is
dy
at the time when
dt
dx
= 390 and y = 6,250?
dt
6,250 feet from the observer? That is, what is
This problem is an example of critically damped harmonic motion.
A hollow steel ball weighing 4 pounds is suspended from a spring. This stretches the spring
feet. The ball is started in motion from the equilibrium position with a downward velocity of 5
feet per second. The air resistance (in pounds) of the moving ball numerically equals 4 times
its velocity (in feet per second). Suppose that after t seconds the ball is y feet below its rest
position. Find y in terms of t.
Take as the gravitational acceleration 32 feet per second per second. (Note that the positive y
direction is down in this problem.)
y =
le
EXERCISE 2.2 An automobile follows a circular road whose radius is 50 m. Let x and y
respectively denote the eastern and northern directions, with origin at the center of the
circle. Suppose the vehicle starts from rest at x = 50 m heading north, and its speed
depends on the distance s it travels according to v=0.5s-0.0025s², where s is measured
in meters and v is in meters per second. It is known that the tires will begin to skid when
the total acceleration of the vehicle is 0.6g. Where will the automobile be and how fast
will it be going when it begins to skid? Describe the position in terms of the angle of the
radial line relative to the x axis.
Chapter 7 Solutions
Differential Equations: An Introduction to Modern Methods and Applications
Ch. 7.1 - For each of the systems in Problems 1 through 18:...Ch. 7.1 - For each of the systems in Problems 1 through 18:...Ch. 7.1 - For each of the systems in Problems 1 through 18:...Ch. 7.1 - For each of the systems in Problemsthrough:
Find...Ch. 7.1 - For each of the systems in Problems 1 through 18:...Ch. 7.1 - For each of the systems in Problems 1 through 18:...Ch. 7.1 - For each of the systems in Problemsthrough:
Find...Ch. 7.1 - For each of the systems in Problems 1 through 18:...Ch. 7.1 - For each of the systems in Problemsthrough:
Find...Ch. 7.1 - For each of the systems in Problems 1 through 18:...
Ch. 7.1 - For each of the systems in Problems 1 through 18:...Ch. 7.1 - For each of the systems in Problems 1 through 18:...Ch. 7.1 - For each of the systems in Problems 1 through 18:...Ch. 7.1 - For each of the systems in Problems 1 through 18:...Ch. 7.1 - For each of the systems in Problemsthrough:
Find...Ch. 7.1 - For each of the systems in Problems 1 through 18:...Ch. 7.1 - For each of the systems in Problems 1 through 18:...Ch. 7.1 - For each of the systems in Problemsthrough:
Find...Ch. 7.1 -
Consider the equations of motion of an undamped...Ch. 7.1 - The motion of a certain undamped pendulum is...Ch. 7.1 - Consider the pendulum equations dxdt=y,dydt=6sinx....Ch. 7.1 - Prob. 22PCh. 7.1 - Given that x=(t),y=(t) is a solution of the...Ch. 7.1 - Prove that, for the system...Ch. 7.1 - Prove that if a trajectory starts at a noncritical...Ch. 7.1 - Assuming that the trajectory corresponding to a...Ch. 7.2 - In each of Problems 1 through 20: (a) Determine...Ch. 7.2 - In each of Problems through
Determine all...Ch. 7.2 - In each of Problems 1 through 20: (a) Determine...Ch. 7.2 - In each of Problems 1 through 20: (a) Determine...Ch. 7.2 - In each of Problems through
Determine all...Ch. 7.2 - In each of Problems 1 through 20: (a) Determine...Ch. 7.2 - In each of Problems 1 through 20: (a) Determine...Ch. 7.2 - In each of Problems 1 through 20: (a) Determine...Ch. 7.2 - In each of Problems through
Determine all...Ch. 7.2 - In each of Problems through
Determine all...Ch. 7.2 - In each of Problems through
Determine all...Ch. 7.2 - In each of Problems 1 through 20: (a) Determine...Ch. 7.2 - In each of Problems through
Determine all...Ch. 7.2 - In each of Problems through
Determine all...Ch. 7.2 - In each of Problems 1 through 20: (a) Determine...Ch. 7.2 - In each of Problems 1 through 20: (a) Determine...Ch. 7.2 - In each of Problems 1 through 20: (a) Determine...Ch. 7.2 - In each of Problems 1 through 20: (a) Determine...Ch. 7.2 - In each of Problems 1 through 20: (a) Determine...Ch. 7.2 - In each of Problems through
Determine all...Ch. 7.2 - Consider the autonomous system dxdt=y,dydt=x+2x3....Ch. 7.2 - Consider the autonomous system
...Ch. 7.2 - The equations of motion of a certain nonlinear...Ch. 7.2 - Theorem 7.2.2 provides no information about the...Ch. 7.2 - In this problem, we show how small changes in the...Ch. 7.2 - In this problem, we show how small changes in the...Ch. 7.2 - A generalization of the damped pendulum equation...Ch. 7.3 - Each of Problems 1 through 6 can be interpreted as...Ch. 7.3 - Each of Problems 1 through 6 can be interpreted as...Ch. 7.3 - Each of Problems 1 through 6 can be interpreted as...Ch. 7.3 - Each of Problems 1 through 6 can be interpreted as...Ch. 7.3 - Each of Problems 1 through 6 can be interpreted as...Ch. 7.3 - Each of Problems 1 through 6 can be interpreted as...Ch. 7.3 - Show that (1X+2Y)24(1212)XY=(1X2Y)2+412XY. Hence...Ch. 7.3 - Consider the system (2) in the text, and assume...Ch. 7.3 - Consider the system (3) in Example 1 of the text....Ch. 7.3 - The system x=yy=yx(x0.15)(x3) Results from an...Ch. 7.3 - Bifurcation points. Consider the system...Ch. 7.3 - Bifurcation points. Consider the system
Where is...Ch. 7.3 - Bifurcation points. Consider the system
Where is...Ch. 7.3 - Bifurcation points. Consider the system
Where is...Ch. 7.3 - In each of Problem 15 and 16: a) Find the critical...Ch. 7.3 - In each of Problem 15 and 16:
Find the critical...Ch. 7.3 - Suppose that a certain pair of competing species...Ch. 7.4 - Each of Problems 1 through 5 can be interpreted as...Ch. 7.4 - Each of Problems 1 through 5 can be interpreted as...Ch. 7.4 - Each of Problems 1 through 5 can be interpreted as...Ch. 7.4 - Each of Problems 1 through 5 can be interpreted as...Ch. 7.4 - Each of Problems 1 through 5 can be interpreted as...Ch. 7.4 - In this problem, we examine the phase difference...Ch. 7.4 - a) Find the ratio of the amplitudes of the...Ch. 7.4 -
Find the period of the oscillations of the prey...Ch. 7.4 - Consider the system
Where and are positive...Ch. 7.4 - The average size of the prey and predator...Ch. 7.4 - In Problems 11 and 12, we consider the effect of...Ch. 7.4 - In Problems 11 and 12, we consider the effect of...Ch. 7.4 - In the Lotka-Volterra equations, the interaction...Ch. 7.4 - Harvesting in a Predator-Prey Relationship. In a...Ch. 7.4 - Harvesting in a Predator-Prey Relationship. In a...Ch. 7.4 - Harvesting in a Predator-Prey Relationship. In a...Ch. 7.5 - In each of Problems through , an autonomous...Ch. 7.5 - In each of Problems 1 through 6, an autonomous...Ch. 7.5 - In each of Problems 1 through 6, an autonomous...Ch. 7.5 - In each of Problems 1 through 6, an autonomous...Ch. 7.5 - In each of Problems through , an autonomous...Ch. 7.5 - In each of Problems 1 through 6, an autonomous...Ch. 7.5 - If x=rcos,y=rsin, show that...Ch. 7.5 - (a) Show that the system has periodic solutions...Ch. 7.5 - Determine the periodic solutions, if any, of the...Ch. 7.5 - Using Theorem, show that the linear autonomous...Ch. 7.5 - In each of Problems 11 and 12, show that the given...Ch. 7.5 - In each of Problems and , show that the given...Ch. 7.5 - Prob. 13PCh. 7.5 -
By examining the graphs of vs. in Figures , , ...Ch. 7.5 - The equation u(113u2)u+u=0 Is often called the...Ch. 7.5 - Consider the system of equations...Ch. 7.5 - Consider the van der Pol system x=y,y=x+(1x2)y,...Ch. 7.5 - Problems 18 and 19 extend the consideration of the...Ch. 7.5 - Problems 18 and 19 extend the consideration of the...Ch. 7.5 - There are certain chemical reactions in which the...Ch. 7.5 - The system
Is a special case of the...Ch. 7.6 - Problems through ask you to fill in some of the...Ch. 7.6 - Problems through ask you to fill in some of the...Ch. 7.6 -
Ch. 7.6 - Consider the ellipsoid
.
Calculate
along...Ch. 7.6 - In each of Problems 5 through 7, carry out the...Ch. 7.6 - In each of Problems 5 through 7, carry out the...Ch. 7.6 - In each of Problems 5 through 7, carry out the...Ch. 7.6 - For certain intervals, or windows, the Lorenz...Ch. 7.6 - Now consider values of r slightly larger than...Ch. 7.P1 - Assume that , that is, the total size of the...Ch. 7.P1 - The triangular region in the SI-plane is depicted...Ch. 7.P1 - If epidemics are identified with solution...Ch. 7.P1 - Find an equation of the form satisfied by the...Ch. 7.P1 - In the SIR system (1), describe qualitatively the...Ch. 7.P1 - Vaccinated individual are protected from acquiring...Ch. 7.P1 - Use the equation to reduce the SIRS model (3) to...Ch. 7.P2 - Consider again the system
(i)
Which...Ch. 7.P2 - Consider the system dxdt=x(1xy),dydt=y(0.80.6yx),...Ch. 7.P2 - Consider the system (i) in Problem 1, and assume...Ch. 7.P2 - Aconstant-yield model, applied to species x,...Ch. 7.P3 - a) Show that there are no critical points when...Ch. 7.P3 - a) Let c=1.3. Find the critical points and the...Ch. 7.P3 - The limit cycle found in Problem 2 comes into...Ch. 7.P3 -
Let. Find the critical points and the...Ch. 7.P3 -
Let. Find the critical points and the...
Additional Math Textbook Solutions
Find more solutions based on key concepts
69. Get Started Early! Mitch and Bill are both age 75. When Mitch was 25 years old, he began depositing $1000 p...
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
In Problems 41 through 44, a differential equation and a non-trivial solution f are given. Find a second linear...
Fundamentals of Differential Equations and Boundary Value Problems
19-22: Investment Plans. Use the savings plan formula to answer the following questions.
19. At age 25, YOU ...
Using & Understanding Mathematics: A Quantitative Reasoning Approach (7th Edition)
Solve each problem involving proportions. Price of Gasoline If 6 gallons of premium unleaded gasoline cost $17....
Mathematical Ideas (13th Edition) - Standalone book
Checkpoint1
Use the substitution method to solve this system:
Answers to Checkpoint exercises are found at the...
Mathematics with Applications In the Management, Natural, and Social Sciences (12th Edition)
Convert each of the following percents to decimals: 78%
Mathematics All Around (6th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- A stamped sheet steel plate is shown in Figure 164. Compute dimensions AF to 3 decimal places. All dimensions are in inches. A=_B=_C=_D=_E=_F=_arrow_forward3.) Imagine a string that is fixed at both ends (for example, a guitar string). When plucked, the string forms a standing wave. The displacement, u(x, t), of the string varies with position x and time t. Suppose a,t) = 2sin(xx)sin() for 0 0. At a fixed point in time, the string forms a wave on 10, 11. Alternatively, if you focus on a point on the string (fix a value of r), that point oscillates up and down in time. a.) What is the period of the motion in time? За.) du 3b.) dt b.) Find the rate of change of the displacement with respect to time at a constant position (which is the vertical velocity of a point on the string.) 3c.) x = c.) At a fixed time, what point on the string is moving fastest? 3d.) t = d.) At a fixed position on the string, when is the string moving fastest? du 3e.) e.) Find the rate of change of displacement with respect to position at a constant time (which is the slope of the string.) 3f.) r =, f.) At a fixed time, where is the slope of the string the greatest?arrow_forwardAccording to the NIH, normal blood pressure is below 120/80, moderately high is from 140/90 to 159/99 and severe is higher than 160/100. The blood pressure of a particular person is modeled approximately by: P = 135+30cos(2.5(t)pi) where P is pressure in millimeters of mercury t seconds after the heart contracts. 1) Sketch one wave (starting at t = 0) of the cosine wave. Be sure to label your axes appropriately with P and t, as well as appropriate scales. Your P axis does not have to start at zero (it may begin at the minimum of the wave). Also clearly label five points on your cosine wave, which correspond to the minimums, maximums and zeros of the wave. Each point should have two coordinates. 2) What is the person’s blood pressure as an approximate ratio of two numbers? 3) What is the period of the heartbeat? 4) What is the pulse rate in beats per minute?arrow_forward
- According to the Old Farmer’s Almanac, in Anchorage, Alaska, the number of hours of sunlight on the summer solstice of 2010 was 19.42 and the number of hours of sunlight on the winter solstice was 5.48. (a) Find a sinusoidal function of the form y=Asin(ωx- ϕ)+B that models the data. (b) Use the function found in part (a) to predict the number of hours of sunlight on April 1,the 91st day of the year. (c) Draw a graph of the function found in part (a). *(d) Look up the number of hours of sunlight for April 1 in the Old Farmer’s Almanac,and compare the actual hours of daylight to the results found in part (c).arrow_forward4. In biology the predator-prey model is used to predict the number of prey animals, R, at a particular time t, in years. This number is cyclic, fluctuating with the number of predators. The number of rabbits, R, in a certain region is given by the equation R(t) = 2000 sin(t) + 5000. a) Sketch the graph of this relationship b) Determine how many rabbits there will be in 4 years.arrow_forwardThe number of hours of daylight each day for a particular city can be modeled using the sinusoidal function s(m)=5sin(2π/12m−π/2)+13 , where s is the number of hours of sunlight per day, and m represents the month of the year, with m=1 corresponding to January, m=2 corresponding to February, etc. What is the number of hours of daylight in the longest day of the year? A.8 hours B. 13 hours C.18 Hours D.24 hoursarrow_forward
- When a spring oscillates with decreasing amplitude (because it is being damped by friction, for example), its motion is often modeled as the product of a trigonometric function (the oscillation) and an exponential function (the decay of amplitude). Suppose that the displacement of a particular damped spring is s(t) 2e-1.8t cos(2πt), with s in inches and t in seconds. a) Find the spring's velocity with respect to t: v(t) = -4 pi ^(-1.8t) sin(2 pi ! t)-3.6e^(-1.8t) cos(2 pi t) That's not it. in/sec .-1.8t -4π¯¯ = -1.8t sin(2πt) — 3.6e¯ Preview v(t) = cos(2π. t) in/secarrow_forwardState the amplitude, period, phase shift and range for the sinusoid g(x) = -3sin(5x-11/4) + 19arrow_forwardAn angle modulated signal has the form V(t) = 100 cos(2nf t+4 sin 2000 t) when f =10 MHz.arrow_forward
- The manner in which a string is plucked determines the mixture of harmonic amplitudes in the resulting wave. Consider a string exactly 1/2-m long that is fixed at both its ends located at x = 0.0 and x = m. The first five harmonics of this string have wavelengths λ₁ = 1.0 m, λ₂ = 1/2 m, λ = 1/3 m, 14 = 1/4 m, and λ5 = 1/5 m. According to Fourier's theorem, any shape of this string can be formed by a sum of its harmonics, with each harmonic having its own unique amplitude A. We limit the sum to the first five harmonics in the expression m D(x) = m An sin A, (²x) n=1 and D is the displacement of the string at a time t = 0. Imagine plucking this string at its midpoint (Fig. below (a)) or at a point two-thirds from the left end (Fig. below (b)). Use Excel, MATLAB, or other graphing software, to create two plots showing that the above expression can fairly accurately represent the shape in Fig. (a), if A₁ = 1.00, A₂ = 0.00, A3 = -0.11, A4 = 0.00, and A5 = 0.040 and in (b), if A₁ = 0.87, A₂…arrow_forwardA sine function has an amplitude of 7, a period of 720°, and range {y € R-2 ≤ y ≤ 12}. Identify the correct equation of this function. y = 5 sin(70) + 1/2 y = 7 sin(0) + 5 y = sin(70) + 5 y = 5 sin(0) + 7arrow_forwardAlex is measuring the time-averaged velocity components in a pump using a laser Doppler velocimeter (LDV). Since the laser beams are aligned with the radial and tangential directions of the pump, he measures the ur and u? com ponents of velocity. At r = 5.20 in and ? = 30.0°, ur = 2.06 ft/s and u? = 4.66 ft/s. Unfortunately, the data analysis program requires input in Cartesian coordinates (x, y) in feet and (u, ?) in ft/s. Help Alex transform his data into Cartesian coordinates. Specifically, calculate x, y, u, and ? at the given data point.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Fundamental Trigonometric Identities: Reciprocal, Quotient, and Pythagorean Identities; Author: Mathispower4u;https://www.youtube.com/watch?v=OmJ5fxyXrfg;License: Standard YouTube License, CC-BY