
Concept explainers
Twelve tasks, with times and precedence requirements as shown in the following table, are 10 be assigned to workstations using a cycle time of 1.5 minutes. Two heuristic rules will be tried: (1) greatest positional weight, and (2) most following tasks. In each case, the tiebreaker will be shortest processing time.
a. Draw the precedence diagram for this line.
b. Assign tasks to stations under each of the two rules.
c. Compute the percentage of idle tune fox each rule.
a)
To draw: The precedence diagram.
Answer to Problem 6P
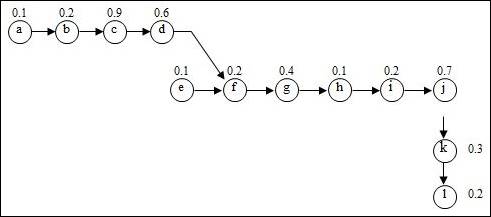
Precedence diagram:
Explanation of Solution
Given information:
| Task | Duration (minutes) | Immediate (Predecessor) |
| a | 0.1 | Nil |
| b | 0.2 | a |
| c | 0.9 | b |
| d | 0.6 | c |
| e | 0.1 | Nil |
| f | 0.2 | d, e |
| g | 0.4 | f |
| h | 0.1 | g |
| i | 0.2 | h |
| j | 0.7 | i |
| k | 0.3 | j |
| l | 0.2 | k |
Cycle time = 1.5 minutes
Precedence diagram:

The precedence diagram is drawn circles and arrows. The tasks are represented in circles and weights for each task are represented outside the circle. The arrows are represented to show which task is preceding the other task and so on.
b)
1)
To assign: Tasks on the basis of greatest positional weight.
Explanation of Solution
Given information:
| Task | Duration (minutes) | Immediate (Predecessor) |
| a | 0.1 | Nil |
| b | 0.2 | a |
| c | 0.9 | b |
| d | 0.6 | c |
| e | 0.1 | Nil |
| f | 0.2 | d, e |
| g | 0.4 | f |
| h | 0.1 | g |
| i | 0.2 | h |
| j | 0.7 | i |
| k | 0.3 | j |
| l | 0.2 | k |
Cycle time = 1.5 minutes
The number of following tasks, calculation of positional weight, processing time for each task is shown below.
| Task | Following tasks | Number of following tasks | Calculation of positional weight | Positional weight | Processing time |
| a | b, c, d, f, g, h, i, j, k, l | 10 | 0.1 + 0.2 + 0.9 + 0.6 + 0.2 + 0.4 + 0.1 + 0.2 + 0.7+ 0.3 + 0.2 | 3.9 | 0.1 |
| b | c, d, f, g, h, i, j, k, l | 9 | 0.2 + 0.9 + 0.6 + 0.2 + 0.4 + 0.1 + 0.2 + 0.7+ 0.3 + 0.2 | 3.8 | 0.2 |
| c | d, f, g, h, i, j, k, l | 8 | 0.9 + 0.6 + 0.2 + 0.4 + 0.1 + 0.2 + 0.7+ 0.3 + 0.2 | 3.6 | 0.9 |
| d | f, g, h, i, j, k, l | 7 | 0.6 + 0.2 + 0.4 + 0.1 + 0.2 + 0.7+ 0.3 + 0.2 | 2.7 | 0.6 |
| e | f, g, h, i, j, k, l | 7 | 0.1 + 0.2 + 0.4 + 0.1 + 0.2 + 0.7+ 0.3 + 0.2 | 2.2 | 0.1 |
| f | g, h, i, j, k, l | 6 | 0.2 + 0.4 + 0.1 + 0.2 + 0.7+ 0.3 + 0.2 | 2.1 | 0.2 |
| g | h, i, j, k, l | 5 | 0.4 + 0.1 + 0.2 + 0.7+ 0.3 + 0.2 | 1.9 | 0.4 |
| h | i, j, k, l | 4 | 0.1 + 0.2 + 0.7+ 0.3 + 0.2 | 1.5 | 0.1 |
| i | j, k, l | 3 | 0.2 + 0.7+ 0.3 + 0.2 | 1.4 | 0.2 |
| j | k, l | 2 | 0.7+ 0.3 + 0.2 | 1.2 | 0.7 |
| k | l | 1 | 0.3 + 0.2 | 0.5 | 0.3 |
| l | Nil | 0 | 0.2 | 0.2 | 0.2 |
Assigning tasks to workstations:
| Workstation number | Eligible task | Assigned task | Task time | Unassigned cycle time | Reason |
| 1.5 | |||||
| 1 | a, e | a | 0.1 | 1.4 | Task 'a' has highest positional weight |
| b, e | b | 0.2 | 1.2 | Task 'b' has highest positional weight | |
| c, e | c | 0.9 | 0.3 | Task 'c' has highest positional weight | |
| d, e | e | 0.1 | 0.2 | Task 'e' is the only eligible task available | |
| d | None | 0.2 (Idle time) | The task time is greater than the unassigned cycle time. | ||
| 1.5 | |||||
| 2 | d | d | 0.6 | 0.9 | Task 'd' is the only eligible task available |
| f | f | 0.2 | 0.7 | Task 'f' is the only eligible task available | |
| g | g | 0.4 | 0.3 | Task 'g' is the only eligible task available | |
| h | h | 0.1 | 0.2 | Task 'h' is the only eligible task available | |
| i | i | 0.2 | 0 | Task 'i' is the only eligible task available | |
| 1.5 | |||||
| 3 | j | j | 0.7 | 0.8 | Task 'j' is the only eligible task available |
| k | k | 0.3 | 0.5 | Task 'k' is the only eligible task available | |
| l | l | 0.2 | 0.3 | Task 'l' is the only eligible task available | |
| 0.3 (Idle time) | All tasks completed |
Overview of tasks assignment:
| Workstation | Assigned tasks | Total cycle time used | Idle time |
| 1 | a, b, c, e | 1.3 | 0.2 |
| 2 | d, f, g, h, i | 1.5 | 0 |
| 3 | j, k, l | 1.2 | 0.3 |
2)
To assign: Tasks on the basis of most following tasks.
Explanation of Solution
Given information:
| Task | Duration (minutes) | Immediate (Predecessor) |
| a | 0.1 | Nil |
| b | 0.2 | a |
| c | 0.9 | b |
| d | 0.6 | c |
| e | 0.1 | Nil |
| f | 0.2 | d, e |
| g | 0.4 | f |
| h | 0.1 | g |
| i | 0.2 | h |
| j | 0.7 | i |
| k | 0.3 | j |
| l | 0.2 | k |
Cycle time = 1.5 minutes
The number of following tasks, calculation of positional weight, processing time for each task is shown below.
| Task | Following tasks | Number of following tasks | Calculation of positional weight | Positional weight | Processing time |
| a | b, c, d, f, g, h, i, j, k, l | 10 | 0.1 + 0.2 + 0.9 + 0.6 + 0.2 + 0.4 + 0.1 + 0.2 + 0.7+ 0.3 + 0.2 | 3.9 | 0.1 |
| b | c, d, f, g, h, i, j, k, l | 9 | 0.2 + 0.9 + 0.6 + 0.2 + 0.4 + 0.1 + 0.2 + 0.7+ 0.3 + 0.2 | 3.8 | 0.2 |
| c | d, f, g, h, i, j, k, l | 8 | 0.9 + 0.6 + 0.2 + 0.4 + 0.1 + 0.2 + 0.7+ 0.3 + 0.2 | 3.6 | 0.9 |
| d | f, g, h, i, j, k, l | 7 | 0.6 + 0.2 + 0.4 + 0.1 + 0.2 + 0.7+ 0.3 + 0.2 | 2.7 | 0.6 |
| e | f, g, h, i, j, k, l | 7 | 0.1 + 0.2 + 0.4 + 0.1 + 0.2 + 0.7+ 0.3 + 0.2 | 2.2 | 0.1 |
| f | g, h, i, j, k, l | 6 | 0.2 + 0.4 + 0.1 + 0.2 + 0.7+ 0.3 + 0.2 | 2.1 | 0.2 |
| g | h, i, j, k, l | 5 | 0.4 + 0.1 + 0.2 + 0.7+ 0.3 + 0.2 | 1.9 | 0.4 |
| h | i, j, k, l | 4 | 0.1 + 0.2 + 0.7+ 0.3 + 0.2 | 1.5 | 0.1 |
| i | j, k, l | 3 | 0.2 + 0.7+ 0.3 + 0.2 | 1.4 | 0.2 |
| j | k, l | 2 | 0.7+ 0.3 + 0.2 | 1.2 | 0.7 |
| k | l | 1 | 0.3 + 0.2 | 0.5 | 0.3 |
| l | Nil | 0 | 0.2 | 0.2 | 0.2 |
Assigning tasks to workstations:
| Workstation number | Eligible task | Assigned task | Task time | Unassigned cycle time | Reason |
| 1.5 | |||||
| 1 | a, e | a | 0.1 | 1.4 | Task 'a' has the most following tasks |
| b, e | b | 0.2 | 1.2 | Task 'b' has the most following tasks | |
| c, e | c | 0.9 | 0.3 | Task 'c' has the most following tasks | |
| d, e | e | 0.1 | 0.2 | Task 'e' is the only eligible task available | |
| d | None | 0.2 (Idle time) | The task time is greater than the unassigned cycle time. | ||
| 1.5 | |||||
| 2 | d | d | 0.6 | 0.9 | Task 'd' is the only eligible task available |
| f | f | 0.2 | 0.7 | Task 'f' is the only eligible task available | |
| g | g | 0.4 | 0.3 | Task 'g' is the only eligible task available | |
| h | h | 0.1 | 0.2 | Task 'h' is the only eligible task available | |
| i | i | 0.2 | 0 | Task 'i' is the only eligible task available | |
| 1.5 | |||||
| 3 | j | j | 0.7 | 0.8 | Task 'j' is the only eligible task available |
| k | k | 0.3 | 0.5 | Task 'k' is the only eligible task available | |
| l | l | 0.2 | 0.3 | Task 'l' is the only eligible task available | |
| 0.3 (Idle time) | All tasks completed |
Overview of tasks assignment:
| Workstation | Assigned tasks | Total cycle time used | Idle time |
| 1 | a, b, c, e | 1.3 | 0.2 |
| 2 | d, f, g, h, i | 1.5 | 0 |
| 3 | j, k, l | 1.2 | 0.3 |
c)
To determine: The percentage of idle time.
Answer to Problem 6P
Explanation of Solution
Formula to calculate percentage of idle time:
Calculation of percentage of idle time:
The solutions for most following tasks rule and highest positional weight is same. Hence, the percentage of idle time will also be the same.
The percentage of idle time is 11.11%.
Want to see more full solutions like this?
Chapter 6 Solutions
Operations Management
- Employee In-Service Training ASSIGNMENT: In-Service Training. The intern is required to plan and implement two in-service training sessions for employees. Each in-service should last at least 10 but not more than 30 minutes and should be given to all employees affected. The preceptor or supervisor/unit manager must approve all in-service topics. 1) One presentation should be related to a policy or procedure of any kind (e.g. proper use of equipment); 2) The second presentation must be related to sanitation or safety. For each in-service presentation, the intern must develop a written class plan and a visual aid (may be a handout, poster, PowerPoint slide presentation, etc.) appropriate to the life experiences, cultural diversity and educational background of the target audience. The intern must also measure behavior change. Note, this cannot be measured by a written pre- and post- test. That would be measuring knowledge. The intern mustactually observe and document that the learners…arrow_forwardFor a dietary manager in a nursing home to train a dietary aidearrow_forwardDietary Management in a Nursing Home. As detailed as possible.arrow_forward
- For dietary management in a nursing home. As detailed as possible.arrow_forwardA small furniture manufacturer produces tables and chairs. Each product must go through three stages of the manufacturing process – assembly, finishing, and inspection. Each table requires 3 hours of assembly, 2 hours of finishing, and 1 hour of inspection. The profit per table is $120 while the profit per chair is $80. Currently, each week there are 200 hours of assembly time available, 180 hours of finishing time, and 40 hours of inspection time. Linear programming is to be used to develop a production schedule. Define the variables as follows: T = number of tables produced each week C= number of chairs produced each week According to the above information, what would the objective function be? (a) Maximize T+C (b) Maximize 120T + 80C (c) Maximize 200T+200C (d) Minimize 6T+5C (e) none of the above According to the information provided in Question 17, which of the following would be a necessary constraint in the problem? (a) T+C ≤ 40 (b) T+C ≤ 200 (c) T+C ≤ 180 (d) 120T+80C ≥ 1000…arrow_forwardAs much detail as possible. Dietary Management- Nursing Home Don't add any fill-in-the-blanksarrow_forward
- Menu Planning Instructions Use the following questions and points as a guide to completing this assignment. The report should be typed. Give a copy to the facility preceptor. Submit a copy in your Foodservice System Management weekly submission. 1. Are there any federal regulations and state statutes or rules with which they must comply? Ask preceptor about regulations that could prescribe a certain amount of food that must be kept on hand for emergencies, etc. Is the facility accredited by any agency such as Joint Commission? 2. Describe the kind of menu the facility uses (may include standard select menu, menu specific to station, non-select, select, room service, etc.) 3. What type of foodservice does the facility have? This could be various stations to choose from, self-serve, 4. conventional, cook-chill, assembly-serve, etc. Are there things about the facility or system that place a constraint on the menu to be served? Consider how patients/guests are served (e.g. do they serve…arrow_forwardWork with the chef and/or production manager to identify a menu item (or potential menu item) for which a standardized recipe is needed. Record the recipe with which you started and expand it to meet the number of servings required by the facility. Develop an evaluation rubric. Conduct an evaluation of the product. There should be three or more people evaluating the product for quality. Write a brief report of this activity • Product chosen and the reason why it was selected When and where the facility could use the product The standardized recipe sheet or card 。 o Use the facility's format or Design one of your own using a form of your choice; be sure to include the required elements • • Recipe title Yield and portion size Cooking time and temperature Ingredients and quantities Specify AP or EP Procedures (direction)arrow_forwardASSIGNMENT: Inventory, Answer the following questions 1. How does the facility survey inventory? 2. Is there a perpetual system in place? 3. How often do they do a physical inventory? 4. Participate in taking inventory. 5. Which type of stock system does the facility use? A. Minimum stock- includes a safety factor for replenishing stock B. Maximum stock- equal to a safety stock plus estimated usage (past usage and forecasts) C. Mini-max-stock allowed to deplete to a safety level before a new order is submitted to bring up inventory up to max again D. Par stock-stock brought up to the par level each time an order is placed regardless of the amount on hand at the time of order E. Other-(describe) Choose an appropriate product and determine how much of an item should be ordered. Remember the formula is: Demand during lead time + safety stock = amount to order Cost out an inventory according to data supplied. Remember that to do this, you will need to take an inventory, and will need to…arrow_forward
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,

