Chapter 6, Problem 6.122P

To determine

The steady flow rates in each pipe and the difference in both the results.

Answer to Problem 6.122P

$\begin{array}{l}{Q}_1=0.1264m^3/s\\ Q_2=0.0879m^3/s\\ Q_3=0.0291m^3/s\end{array}$

The flow rates found in this part is 5.2 times lower than that of part P6.121. It is because the flow rate is dependent on the cross-sectional area. Therefore, reducing the diameter from 28 to 15 will decrease the amount of flow rate.

Explanation of Solution

Given information:

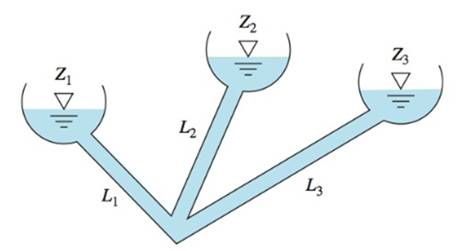
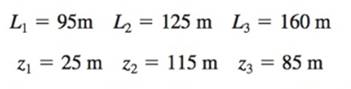
Diameter of all pipes are $15cm$ and roughness $\in =1mm$

At three reservoir junction, if all flows are considered positive towards the junction, then

$Q_1+Q_2+Q_3=0\to \left(1\right)$

Assuming the gauge pressure $p_1=p_2=p_3=0$, the head loss $\Delta h$ across each pipe is equal to,

$\Delta h=f\left(\frac{L}{D}\right)\left(\frac{V^2}{2g}\right)=z-h_j$

$f$ - Friction factor

$L$ - Length of the pipe

$D$ - Diameter of the pipe

$V$ -Velocity of the flow

$z$ - Elevation

To solve this type of problems, we should guess the position of $h_j$ and solve the above mentioned equation to find the relevant velocities and flow rates, iterating until the flow rates satisfies the equation 1.

If the $h_j$ guessed was too high, then the sum of equation (1) will be negative, therefore we have to reduce $h_j$ and vice versa.

Calculation:

First of all,

Guess $h_a=85m$, therefore

${\left(h_f\right)}_1=z_1-h_a=25m-85m=-60m$

The roughness ratio for all pipes will be,

$\frac{\in }{d}=\frac{1\times {10}^{-3}m}{0.15m}=6.667\times {10}^{-3}$

To find Reynolds’s number,

$R_e=\frac{DV}{\nu }$ Try $V_1=10m/s$

Therefore,

${\left(R_e\right)}_1=\frac{DV}{\nu }=\frac{\left(0.15m\right)\left(10m/s\right)}{1.01\times {10}^{-6}{m}^2/s}=1.485\times {10}^6$

The friction factor will be equal to,

$\frac{1}{f^{1/2}}\approx -1.8\log \left(\frac{6.9}{R_e}+{\left(\frac{\text{}\in /d}{3.7}\right)}^{1.11}\right)\approx -1.8\log \left(\frac{6.9}{1.485\times {10}^6}+{\left(\frac{\text{}6.667\times {10}^{-3}}{3.7}\right)}^{1.11}\right)=0.0333$

Therefore, according to the below equation

$\Delta h=f\left(\frac{L}{D}\right)\left(\frac{V^2}{2g}\right)=z-h_j$ $\begin{array}{l}{\left(h_f\right)}_1=f\left(\frac{L}{D}\right)\left(\frac{V^2}{2g}\right)=\left(0.0333\right)\left(\frac{95m}{0.15m}\right)\left(\frac{V_1{}^2}{2\left(9.81\right)}\right)=60m\\ V_1=7.4711m/s\end{array}$

According to the above result, the Reynolds’s number will be

${\left(R_e\right)}_1=\frac{DV}{\nu }=\frac{\left(0.15m\right)\left(7.4711m/s\right)}{1.01\times {10}^{-6}{m}^2/s}=1.11\times {10}^6$

To find the flow rate,

$Q_1=A_1{V}_1=\left[\pi {\left(0.075\right)}^2\left(7.4711m/s\right)\right]=0.131m^3/s$

The flow in pipe 1 is considered as flow away from the junction

Similarly for pipe 2,

${\left(h_f\right)}_2=z_2-h_a=115m-85m=30m$

To find Reynolds’s number,

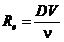Try $V_2=10m/s$

Therefore,

${\left(R_e\right)}_2=\frac{DV}{\nu }=\frac{\left(0.15m\right)\left(10m/s\right)}{1.01\times {10}^{-6}{m}^2/s}=1.485\times {10}^6$

The friction factor will be the same.

$\begin{array}{l}{\left(h_f\right)}_2=f\left(\frac{L}{D}\right)\left(\frac{V^2}{2g}\right)=\left(0.0333\right)\left(\frac{125m}{0.15m}\right)\left(\frac{V_2{}^2}{2\left(9.81\right)}\right)=30m\\ V_1=4.605m/s\end{array}$

According to the above result, the Reynolds’s number will be

${\left(R_e\right)}_2=\frac{DV}{\nu }=\frac{\left(0.15m\right)\left(4.605m/s\right)}{1.01\times {10}^{-6}{m}^2/s}=6.84\times {10}^6$

To find the flow rate,

$Q_2=A_2{V}_2=\left[\pi {\left(0.075\right)}^2\left(4.605m/s\right)\right]=0.0813m^3/s$

The flow in pipe 2 is considered as flow towards the junction.

For pipe 3,

${\left(h_f\right)}_3=z_3-h_a=85m-85m=0$

$Q_3=0$

Therefore,

$Q=Q_2-Q_1=0.0813m^3/s-0.131m^3/s=-0.0497m^3/s$

Hence $h_a$ must be lower than, try $h_a=80m$

${\left(h_f\right)}_1=z_1-h_a=25m-80m=-55m$

Try $V_1=10m/s$

Therefore,

${\left(R_e\right)}_1=\frac{DV}{\nu }=\frac{\left(0.15m\right)\left(10m/s\right)}{1.01\times {10}^{-6}{m}^2/s}=1.485\times {10}^6$

The friction factor will be the same.

$\begin{array}{l}{\left(h_f\right)}_1=f\left(\frac{L}{D}\right)\left(\frac{V^2}{2g}\right)=\left(0.0333\right)\left(\frac{95m}{0.15m}\right)\left(\frac{V_1{}^2}{2\left(9.81\right)}\right)=55m\\ V_1=7.153m/s\end{array}$

According to the above result, the Reynolds’s number will be

${\left(R_e\right)}_1=\frac{DV}{\nu }=\frac{\left(0.15m\right)\left(7.153m/s\right)}{1.01\times {10}^{-6}{m}^2/s}=1.0623\times {10}^6$

To find the flow rate,

$Q_1=A_1{V}_1=\left[\pi {\left(0.075\right)}^2\left(7.153m/s\right)\right]=0.1264m^3/s$

The flow in pipe 1 is considered as flow away from the junction

Similarly for pipe 2,

${\left(h_f\right)}_2=z_2-h_a=115m-80m=35m$

To find Reynolds’s number,

$R_e=\frac{DV}{\nu }$ Try $V_2=10m/s$

Therefore,

${\left(R_e\right)}_1=\frac{DV}{\nu }=\frac{\left(0.15m\right)\left(10m/s\right)}{1.01\times {10}^{-6}{m}^2/s}=1.485\times {10}^6$

The friction factor will be same.

$\begin{array}{l}{\left(h_f\right)}_2=f\left(\frac{L}{D}\right)\left(\frac{V^2}{2g}\right)=\left(0.0333\right)\left(\frac{125m}{0.15m}\right)\left(\frac{V_2{}^2}{2\left(9.81\right)}\right)=35m\\ V_1=4.974m/s\end{array}$

According to the above result, the Reynolds’s number will be

${\left(R_e\right)}_2=\frac{DV}{\nu }=\frac{\left(0.15m\right)\left(4.974m/s\right)}{1.01\times {10}^{-6}{m}^2/s}=0.738\times {10}^6$

To find the flow rate,

$Q_2=A_2{V}_2=\left[\pi {\left(0.075\right)}^2\left(4.974m/s\right)\right]=0.0879m^3/s$

The flow in pipe 2 is considered as flow towards the junction.

Similarly for pipe 3,

${\left(h_f\right)}_3=z_3-h_a=85m-80m=5m$

To find Reynolds’s number,

Try $V_3=1m/s$

Therefore,

${\left(R_e\right)}_3=\frac{DV}{\nu }=\frac{\left(0.15m\right)\left(1m/s\right)}{1.01\times {10}^{-6}{m}^2/s}=1.485\times {10}^5$

The friction factor will be equal to,

$\frac{1}{f^{1/2}}\approx -1.8\log \left(\frac{6.9}{R_e}+{\left(\frac{\text{}\in /d}{3.7}\right)}^{1.11}\right)\approx -1.8\log \left(\frac{6.9}{1.485\times {10}^5}+{\left(\frac{\text{}6.667\times {10}^{-3}}{3.7}\right)}^{1.11}\right)=0.0337$

$\begin{array}{l}{\left(h_f\right)}_3=f\left(\frac{L}{D}\right)\left(\frac{V^2}{2g}\right)=\left(0.0337\right)\left(\frac{160m}{0.15m}\right)\left(\frac{V_3{}^2}{2\left(9.81\right)}\right)=5m\\ V_3=1.652m/s\end{array}$

According to above result, the Reynolds’s number will be

${\left(R_e\right)}_3=\frac{DV}{\nu }=\frac{\left(0.15m\right)\left(1.652m/s\right)}{1.01\times {10}^{-6}{m}^2/s}=2.453\times {10}^5$

To find the flow rate,

$Q_3=A_3{V}_3=\left[\pi {\left(0.075\right)}^2\left(1.652m/s\right)\right]=0.0291m^3/s$

The flow in pipe 3 is considered as flow towards the junction.

Therefore the flow rate will be,

$Q=(Q_2+Q_3)-Q_1=\left(0.0879+0.0291\right)-0.1264=-0.0094m^3/s$

By further iteration, we can get this close to zero, but for now, according to the obtained results, we can say,

$\begin{array}{l}{Q}_1=0.1264m^3/s\\ Q_2=0.0879m^3/s\\ Q_3=0.0291m^3/s\end{array}$

In part P6.121, the flow rate were,

$\begin{array}{l}{Q}_1=0.66m^3/s\\ Q_2=0.459m^3/s\\ Q_3=0.153m^3/s\end{array}$

Therefore, we can say,

$\frac{0.66m^3/s}{0.1264m^3/s}=5.22$

The flow rates found in this part is 5.2 times lower than that of part P6.121. It’s because the flow rate is dependent on the cross-sectional area. Therefore, reducing the diameter from 28 to 15 will decrease the amount of flow rate.

Conclusion:

The flow rates in each pipe is equal to,

$\begin{array}{l}{Q}_1=0.1264m^3/s\\ Q_2=0.0879m^3/s\\ Q_3=0.0291m^3/s\end{array}$

The flow rates are 5.2 times lower than that of part P6.121.