
Concept explainers
a.
To find : The local extrema of the function
a.
Answer to Problem 27E
The maximum is at
Explanation of Solution
Given information :
The given function is
Calculation :
To find the local extrema first find the derivative of
Set
Substitute
Also, substitute
Therefore, the maximum is at
Hence,
The maximum is at
b.
To find : The interval on which the function
b.
Answer to Problem 27E
The function is increasing in the interval
Explanation of Solution
Given information :
The given function is
Calculation :
To find the interval on which the function is increasng first find the derivative of
Set
Use sign chart to get the interval in which the function is increasing
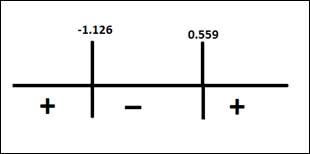
Therefore, the function is increasing in the interval
Hence,
The function is increasing in the interval
c.
To find : The interval on which the function
c.
Answer to Problem 27E
The interval on which the function is decreasing is
Explanation of Solution
Given information :
The given function is
Calculation :
To find the interval on which the function is decreasing first find the derivative of
Set
Use sign chart to get the interval in which the function is decreasing.
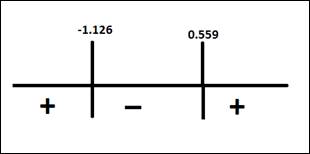
Therefore, the function is decreasing on the interval
Hence,
The function is decreasing in the interval
Chapter 5 Solutions
Calculus: Graphical, Numerical, Algebraic
Additional Math Textbook Solutions
Introductory Statistics
University Calculus: Early Transcendentals (4th Edition)
Elementary Statistics
Elementary Statistics (13th Edition)
Elementary Statistics: Picturing the World (7th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
- The spread of an infectious disease is often modeled using the following autonomous differential equation: dI - - BI(N − I) − MI, dt where I is the number of infected people, N is the total size of the population being modeled, ẞ is a constant determining the rate of transmission, and μ is the rate at which people recover from infection. Close a) (5 points) Suppose ẞ = 0.01, N = 1000, and µ = 2. Find all equilibria. b) (5 points) For the equilbria in part a), determine whether each is stable or unstable. c) (3 points) Suppose ƒ(I) = d. Draw a phase plot of f against I. (You can use Wolfram Alpha or Desmos to plot the function, or draw the dt function by hand.) Identify the equilibria as stable or unstable in the graph. d) (2 points) Explain the biological meaning of these equilibria being stable or unstable.arrow_forwardFind the indefinite integral. Check Answer: 7x 4 + 1x dxarrow_forwardshow sketcharrow_forward
- Find the indefinite integral. Check Answer: 7x 4 + 1x dxarrow_forwardQuestion 1: Evaluate the following indefinite integrals. a) (5 points) sin(2x) 1 + cos² (x) dx b) (5 points) t(2t+5)³ dt c) (5 points) √ (In(v²)+1) 4 -dv ขarrow_forwardFind the indefinite integral. Check Answer: In(5x) dx xarrow_forward
- Find the indefinite integral. Check Answer: 7x 4 + 1x dxarrow_forwardHere is a region R in Quadrant I. y 2.0 T 1.5 1.0 0.5 0.0 + 55 0.0 0.5 1.0 1.5 2.0 X It is bounded by y = x¹/3, y = 1, and x = 0. We want to evaluate this double integral. ONLY ONE order of integration will work. Good luck! The dA =???arrow_forward43–46. Directions of change Consider the following functions f and points P. Sketch the xy-plane showing P and the level curve through P. Indicate (as in Figure 15.52) the directions of maximum increase, maximum decrease, and no change for f. ■ 45. f(x, y) = x² + xy + y² + 7; P(−3, 3)arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





