
Concept explainers
a.
To find: the logistic regression for the data.
a.
Answer to Problem 31E
Explanation of Solution
Given information: Table shows the population of Pennsylvania in each 10 years
between 1830 and 1950.
| Year since 1820 | Population in Thousands |
| 10 | 1348 |
| 20 | 1724 |
| 30 | 2312 |
| 40 | 2906 |
| 50 | 3522 |
| 60 | 4283 |
| 70 | 5258 |
| 80 | 6302 |
| 90 | 7665 |
| 100 | 8720 |
| 110 | 9631 |
| 120 | 9900 |
| 130 | 10,498 |
Calculation:
The logistic regression curve, for population P, t years after 1820 as produced by graphing utility:
b.
To graph: the data in a
b.
Answer to Problem 31E
Explanation of Solution
Given information:
Calculation:
Scatter plot of the table data with
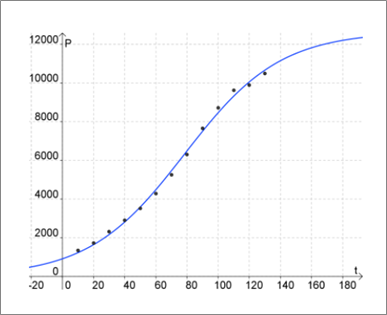
c.
To predict: the Pennsylvania population in the 2000 census.
c.
Answer to Problem 31E
Explanation of Solution
Given information:
Calculation:
2000 is 180 years after 1820, so t = 180 plug that into the regression equation to find the Pennsylvania population in the 2000 census.
d.
To find: in what year was the Pennsylvania population growing the fastest and what significant behavior does the graph of the regression equation exhibit at that point
d.
Answer to Problem 31E
About year 1900.
Explanation of Solution
Given information:
Calculation:
Scatter plot of the table data with
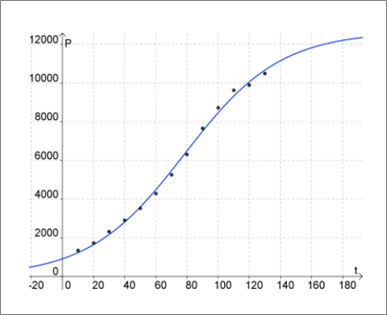
From the graph, the population is increasing the fastest around t =80 .or the year 1900.
The slope of the tangent line at that point is greatest there, in other words, the change in population over the change in time is largest.
The concavity also changes at that point, so it is a point of inflection.
e.
To find: what does the regression equation indicate about the population of Pennsylvania in the long run.
e.
Answer to Problem 31E
In the long term, the equation says the population will stabilize at around 12.66 million.
Explanation of Solution
Given information:
Calculation:
So, in the long term, the equation says the population will stabilize at around 12.66 million.
Chapter 5 Solutions
Calculus: Graphical, Numerical, Algebraic
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
Precalculus
Elementary Statistics (13th Edition)
Elementary Statistics: Picturing the World (7th Edition)
University Calculus: Early Transcendentals (4th Edition)
Algebra and Trigonometry (6th Edition)
- The spread of an infectious disease is often modeled using the following autonomous differential equation: dI - - BI(N − I) − MI, dt where I is the number of infected people, N is the total size of the population being modeled, ẞ is a constant determining the rate of transmission, and μ is the rate at which people recover from infection. Close a) (5 points) Suppose ẞ = 0.01, N = 1000, and µ = 2. Find all equilibria. b) (5 points) For the equilbria in part a), determine whether each is stable or unstable. c) (3 points) Suppose ƒ(I) = d. Draw a phase plot of f against I. (You can use Wolfram Alpha or Desmos to plot the function, or draw the dt function by hand.) Identify the equilibria as stable or unstable in the graph. d) (2 points) Explain the biological meaning of these equilibria being stable or unstable.arrow_forwardFind the indefinite integral. Check Answer: 7x 4 + 1x dxarrow_forwardshow sketcharrow_forward
- Find the indefinite integral. Check Answer: 7x 4 + 1x dxarrow_forwardQuestion 1: Evaluate the following indefinite integrals. a) (5 points) sin(2x) 1 + cos² (x) dx b) (5 points) t(2t+5)³ dt c) (5 points) √ (In(v²)+1) 4 -dv ขarrow_forwardFind the indefinite integral. Check Answer: In(5x) dx xarrow_forward
- Find the indefinite integral. Check Answer: 7x 4 + 1x dxarrow_forwardHere is a region R in Quadrant I. y 2.0 T 1.5 1.0 0.5 0.0 + 55 0.0 0.5 1.0 1.5 2.0 X It is bounded by y = x¹/3, y = 1, and x = 0. We want to evaluate this double integral. ONLY ONE order of integration will work. Good luck! The dA =???arrow_forward43–46. Directions of change Consider the following functions f and points P. Sketch the xy-plane showing P and the level curve through P. Indicate (as in Figure 15.52) the directions of maximum increase, maximum decrease, and no change for f. ■ 45. f(x, y) = x² + xy + y² + 7; P(−3, 3)arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





