Videos
5.53.20 Chemicals are stored in a laboratory with volume V(m3). As a consequence of poor laboratory practices, a hazardous species, A, enters the room air (from inside the room) at a constant rate 
The room is ventilated with clean air ?owing at a constant rate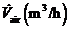 
The average concentration of A in the room air builds up until it reaches a steady-state value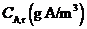 
(a) List at least four situations that could lead to A getting into the room air.
(b) Assume that the A is perfectly mixed with the room air and derive the formula
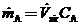
(c) The assumption of perfect mixing is never justi?ed when the enclosed space is a room (as opposed to, say, a stirred reactor). In practice, the concentration of A varies from one point in the room to another: it is relatively high near the point where A enters the room air and relatively low in regions far from that point, including the ventilator outlet duct. If we say that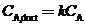 
where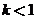 
is a nonideal mixing factor (generally between 0.1 and 0.5, with the lowest value corresponding to the poorest mixing). then the equation of Part (b) becomes
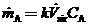
Use this equation and the ideal-gas equation of state to derive the following expression for the average mole fraction of A in the room air:
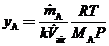
where MA is the molecular weight of A.
(b) The permissible exposure level (PEL) for styrene (M = 104.14) de?ned by the U.S. Occupational Safety and Health Administration is 50 ppm (molar basis).21 An open storage tank in a polymerization laboratory contains styrene. The evaporation rate from this tank is estimated to be 9.0 g/h. Room temperature is 20°C. Assuming that the laboratory air is reasonably well mixed (so that k = 0.5), calculate the minimum ventilation rate (m3/h) required to keep the average styrene concentration at or below the PEL. Then give several reasons why working in the laboratory might still be hazardous if the calculated minimum ventilation rate is used.
(e) Would the hazard level in the situation described in Part (d) increase or decrease if the temperature in the room were to increase? (Increase, decrease, no way to tell.) Explain your answer, citing at least two effects of temperature in your explanation.
Want to see the full answer?
Check out a sample textbook solution
Chapter 5 Solutions
Elementary Principles of Chemical Processes, Binder Ready Version
Additional Engineering Textbook Solutions
INTERNATIONAL EDITION---Engineering Mechanics: Statics, 14th edition (SI unit)
Starting Out with Java: From Control Structures through Data Structures (4th Edition) (What's New in Computer Science)
Database Concepts (8th Edition)
Degarmo's Materials And Processes In Manufacturing
Java: An Introduction to Problem Solving and Programming (8th Edition)
Electric Circuits. (11th Edition)
- Q2/ An adsorption study is set up in laboratory by adding a known amount of activated carbon to six which contain 200 mL of an industrial waste. An additional flask containing 200 mL of waste but no c is run as a blank. Plot the Langmuir isotherm and determine the values of the constants. Flask No. Mass of C (mg) Volume in Final COD Flask (mL) (mg C/L) 1 804 200 4.7 2 668 200 7.0 3 512 200 9.31 4 393 200 16.6 C 5 313 200 32.5 6 238 200 62.8 7 0 200 250arrow_forwardمشر on ۲/۱ Two rods (fins) having same dimensions, one made of brass(k=85 m K) and the other of copper (k = 375 W/m K), having one of their ends inserted into a furnace. At a section 10.5 cm a way from the furnace, the temperature brass rod 120°C. Find the distance at which the same temperature would be reached in the copper rod ? both ends are exposed to the same environment. 22.05 ofthearrow_forward4.59 Using the unilateral z-transform, solve the following difference equations with the given initial conditions. (a) y[n]-3y[n-1] = x[n], with x[n] = 4u[n], y[− 1] = 1 (b) y[n]-5y[n-1]+6y[n-2]= x[n], with x[n] = u[n], y[-1] = 3, y[-2]= 2 Ans. (a) y[n] = -2+9(3)", n ≥ -1 (b) y[n]=+8(2)" - (3)", n ≥ -2arrow_forward
- (30) 6. In a process design, the following process streams must be cooled or heated: Stream No mCp Temperature In Temperature Out °C °C kW/°C 1 5 350 270 2 9 270 120 3 3 100 320 4 5 120 288 Use the MUMNE algorithm for heat exchanger networks with a minimum approach temperature of 20°C. (5) a. Determine the temperature interval diagram. (3) (2) (10) (10) b. Determine the cascade diagram, the pinch temperatures, and the minimum hot and cold utilities. c. Determine the minimum number of heat exchangers above and below the pinch. d. Determine a valid heat exchange network above the pinch. e. Determine a valid heat exchange network below the pinch.arrow_forwardUse this equation to solve it.arrow_forwardQ1: Consider the following transfer function G(s) 5e-s 15s +1 1. What is the study state gain 2. What is the time constant 3. What is the value of the output at the end if the input is a unit step 4. What is the output value if the input is an impulse function with amplitude equals to 3, at t=7 5. When the output will be 3.5 if the input is a unit steparrow_forward
Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education
Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning
Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The