Chapter 4.8, Problem 46E

Solution

To find: The radius of the circumscribed circle.

The radius of the circumscribed circle is approximately 5.76 cm.

Given information:

Given, in a regular polygon all sides have equal length and all angles have equal measure. The required polygon is a regular seven-sided polygon whose sides are 5 cm.

  

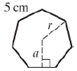
Calculation:

The central angle in a polygon is 360°. This central angle is divided into seven equal parts by the sides i.e., 360/7. Further the apothem divides that angle into half i.e., 360/14=25.71°

Also the apothem divides the sides into two halves i.e., 5/2=2.5 cm

The circumscribed circle passes through the vertices of the polygon with center same as the regular polygon.

The figure representing the data is:

  

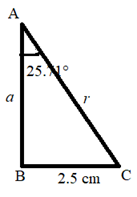
Using the trigonometric function definitions,

  $\begin{array}{c}\sin A=\frac{\text{opposite side}}{\text{hypotenuse}}\\ \sin \left(25.71°\right)=\frac{2.5}{r}\\ r=\frac{2.5}{\sin \left(25.71°\right)}\\ r=\frac{2.5}{0.434}\\ r\approx 5.76\end{array}$

The radius of the circumscribed circle is approximately 5.76 cm.

Conclusion:

The radius of the circumscribed circle is approximately 5.76 cm.