Chapter 4.8, Problem 40E

Solution

To find: The distance of the boat from the harbor.

The distance of the boat from the harbor is approximately 53 nautical miles.

Given information:

Given, a boat leaves harbor and travels at 20 knots on a bearing of 90°. After 2 hr, it changes course to a bearing of 150° and continues at the same speed for another hour. The entire trip is of 3-hr.

Calculation:

The figure representing the data is:

  

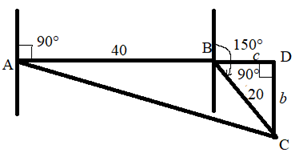
Let the boat start at point A . The boat travels on a bearing of 90° and at 20 knots for 2 hours to reach point B . Here the boat changes the course to a bearing of 150° and travels for 1 hour. Since the boat travels at a speed of 20 knots, the distance travelled in 2 hours is 40 nautical miles and in 1 hour is 20 nautical miles. Extending the line AB to make a perpendicular to point C . Let, $BD=c,CD=b$

From the figure of the triangle BCD, $\angle DBC=60°,\angle BCD=30°,\angle BDC=90°$

Using the trigonometric function definitions,

  $\begin{array}{c}\sin B=\frac{\text{opposite side}}{\text{hypotenuse}}\\ \sin \left(60°\right)=\frac{b}{20}\\ b=20\left(0.866\right)\\ b\approx 17.32\end{array}$

  $\begin{array}{c}\cos B=\frac{\text{adjcent side}}{\text{hypotenuse}}\\ \cos \left(60°\right)=\frac{c}{20}\\ c=20\left(0.5\right)\\ c=10\end{array}$

From the triangle ADC:

  $\begin{array}{l}A{C}^2=A{D}^2+D{C}^2\\ A{C}^2={\left(AB+BD\right)}^2+D{C}^2\\ A{C}^2={\left(40+10\right)}^2+{\left(17.32\right)}^2\\ A{C}^2={\left(50\right)}^2+{\left(17.32\right)}^2\\ A{C}^2=2500+300\\ AC=\sqrt{2800}\\ AC\approx 53\end{array}$

The distance of the boat from the harbor is approximately 53 nautical miles.

Conclusion:

The distance of the boat from the harbor is approximately 53 nautical miles.