Chapter 4.8, Problem 25E

Solution

To find: The distance between the boat and shore.

The distance between the boat and shore is approximately 2931.09 ft.

Given information:

Given, a shoreline runs north south, and a boat is due east of the shoreline. The bearings of the boat from two points on the shore are 110° and 100°. The two points are 550 ft apart.

  

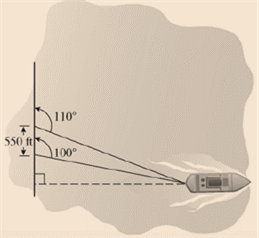
Calculation:

The figure representing the data is:

  

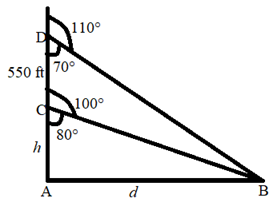
Using definitions of trigonometric functions for the triangle ABC:

  $\begin{array}{c}\tan C=\frac{\text{opposite side}}{\text{adjacent side}}\\ \tan \left(80°\right)=\frac{d}{h}\\ h=\frac{d}{\tan \left(80°\right)}\end{array}$

For triangle ABD:

  $\begin{array}{c}\tan D=\frac{\text{opposite side}}{\text{adjacent side}}\\ \tan \left(70°\right)=\frac{d}{550+h}\\ 550+h=\frac{d}{\tan \left(70°\right)}\\ 550+\frac{d}{\tan \left(80°\right)}=\frac{d}{\tan \left(70°\right)}\\ \frac{d}{\tan \left(70°\right)}-\frac{d}{\tan \left(80°\right)}=550\\ d\approx 2931.09\end{array}$

The distance between the boat and shore is approximately 2931.09 ft.

Conclusion:

The distance between the boat and shore is approximately 2931.09 ft.