
Concept explainers
Two 10-ft3 adiabatic tanks are connected by a valve. Initially, one tank contains water at 450 psia with 10 percent quality, while the second contains water at 15 psia with 75 percent quality. The valve is now opened, allowing the water vapor from the high-pressure tank to move to the low-pressure tank until the pressure in the two becomes equal. Determine the final pressure and the final mass in each tank.
FIGURE P4–142E
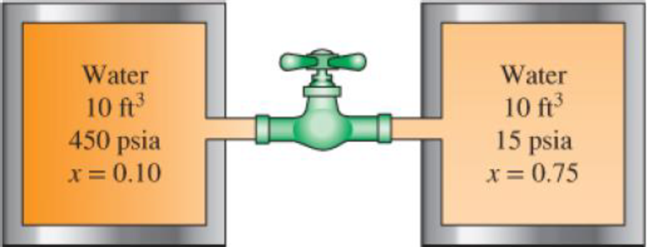
The final pressure of each tank.
The final mass of each tank.
Answer to Problem 142RP
The final pressure of each tank is
The final mass of each tank is
Explanation of Solution
Write the expression for the energy balance equation.
Here, the total energy entering the system is
Simplify Equation (V) and write energy balance relation of two adiabatic tanks.
Here, the heat to be transfer into the system is
Substitute 0 for
Here, the initial mass of tank A is
Write the expression for initial mass of tank A.
Here, the volume of the tank A is
Write the expression for initial mass of tank B.
Here, the volume of the tank B is
Write the expression for total mass of tank.
Write the expression for initial total internal energy contained in both tanks.
Write the expression for initial is equal to final specific internal energy of tank.
Determine the total volume of both the tanks.
Write the expression for initial is equal to final specific volume of tank.
Write the expression for final mass contained in both tanks.
Conclusion:
At initial pressure and quality of initial state for tank A as 450 psia and 0.10, find the value of initial specific volume and specific internal energy of the tank.
Here, the specific volume of saturated liquid for tank A is
Here, the specific internal energy of saturated liquid for tank A is
Substitute
Substitute
At initial pressure and quality of initial state for tank B as 15 psia and 0.75, find the value of initial specific volume and specific internal energy of the tank.
Here, the specific volume of saturated liquid for tank B is
Here, the specific internal energy of saturated liquid for tank B is
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
By above calculation from Table A-5E “saturated water” the final pressure of both tanks as
Thus, the final pressure of each tank is
Substitute
Thus, the final mass of each tank is
Want to see more full solutions like this?
Chapter 4 Solutions
Thermodynamics: An Engineering Approach
- what is an air preheater, what are formulas, and their importance, define the diagram, and give me a script on how to explain the design of an air preheater, and how did values end up in that number. based on standardsarrow_forwardQf, Qa,Qm, Qcon,Qfg, Qbd, Qref,Qloss ( meaning, formula, percentage, and importance of higher value na qf, qa etc)arrow_forwardThe beam is supported by a fixed support at point C and a roller at point A. It also has an internal hinge at point B. The beam supports a point load at point D, a moment at point A and a distributed load on segment BC. a. calculate the support reactions at points A and C b. calculate the internal resultant loadings (N, V, M) at points E and F, which lies in the middle between points A and D P = 4 kip Ma = 5 kip-ft w1 = 3 kip/ft and w2 = 4 kip/ft a = 3 ftarrow_forward
- From the image of the pyramid, I want to find what s1 hat, s2 hat, and s3 hat are. I think s3 hat is just equal to e3 hat right? What about the others?arrow_forward(a) What kind of equation is it?(b) Is it linear or non-linear?(c) Is it a coupled system or uncoupled?arrow_forwardWhat kind of system is presented in Figure 2? Open loop or closed loop?arrow_forward
- What are the control hardware shown in the Figure?arrow_forwardQuestion 1. A tube rotates in the horizontal ry plane with a constant angular velocity w about the z-axis. A particle of mass m is released from a radial distance R when the tube is in the position shown. This problem is based on problem 3.2 in the text. R m 2R Figure 1 x a) Draw a free body diagram of the particle if the tube is frictionless. b) Draw a free body diagram of the particle if the coefficient of friction between the sides of the tube and the particle is = k = p. c) For the case where the tube is frictionless, what is the radial speed at which the particle leaves the tube? d) For the case where there is friction, derive a differential equation that would allow you to solve for the radius of the particle as a function of time. I'm only looking for the differential equation. DO NOT solve it. 1 e) If there is no friction, what is the angle of the tube when the particle exits? • Hint: You may need to solve a differential equation for the last part. The "potentially useful…arrow_forwardQuestion 2. A smooth uniform sphere of mass m and radius r is squeezed between two massless levers, each of length 1, which are inclined at an angle with the vertical. A mechanism at pivot point O ensures that the angles & remain the same at all times so that the sphere moves straight upward. This problem is based on Problem 3-1 in the text. P P r Figure 2 a) Draw appropriate freebody diagrams of the system assuming that there is no friction. b) Draw appropriate freebody diagrams of the system assuming that there is a coefficient of friction between the sphere and the right lever of μ. c) If a force P is applied between the ends of the levers (shown in the diagram), and there is no friction, what is the acceleration of the sphere when = 30°arrow_forward
- If you had a matrix A = [1 2 3; 4 5 6; 7 8 9] and a matrix B = [1 2 3], how would you cross multiply them i.e. what is the cross product of AxB. what would be the cross product of a dyadic with a vector?arrow_forwardProblem 3: The inertia matrix can be written in dyadic form which is particularly useful when inertia information is required in various vector bases. On the next page is a right rectangular pyramid of total mass m. Note the location of point Q. (a) Determine the inertia dyadic for the pyramid P, relative to point Q, i.e., 7%, for unit vectors ₁₁, 2, 3.arrow_forwardCan you solve for v? Also, what is A x uarrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





