
Concept explainers
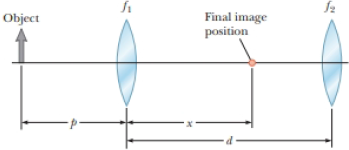
Two converging lenses having focal lengths of f1 = 10.0 cm and f2 = 20.0 cm are placed a distance d = 50.0 cm apart as shown in Figure P35.48. The image due to light passing through both lenses is to be located between the lenses at the position x = 31.0 cm indicated. (a) At what value of p should the object be positioned to the left of the first lens? (b) What is the magnification of the final image? (c) Is the final image upright or inverted? (d) Is the final image real or virtual?
(a)
Answer to Problem 36.78AP
Explanation of Solution
Given info: The focal length of first lens
Write the expression for the final image distance
Here,
Substitute
Write the expression for the thin lens equation.
Here,
Substitute
The image distance to the first lens
Here,
Substitute
Formula to calculate the thin lens equation is,
Here,
Substitute
Conclusion:
Therefore, the value of
(b)
Answer to Problem 36.78AP
Explanation of Solution
Given info: The focal length of first lens
Write the equation for magnification of the first lens.
Write the equation for magnification of the second lens.
Write the equation for magnification of the final image.
Substitute
Substitute
Conclusion:
Therefore, the magnification of the final image is
(c)
Answer to Problem 36.78AP
Explanation of Solution
Given info: The focal length of first lens is
Here, the value of magnification of the final image is
If the magnification is found to be negative
Thus, the image formed is an inverted image.
Conclusion:
Therefore, the final image is inverted.
(d)
Answer to Problem 36.78AP
Explanation of Solution
Given info: The focal length of first lens is
Here, the value of final image distance is
If the value of final image is found to be negative
Thus, the image formed is a virtual image.
Conclusion:
Therefore, the final image is virtual.
Want to see more full solutions like this?
Chapter 36 Solutions
Physics for Scientists and Engineers, Technology Update (No access codes included)
- A 11.8 L gas tank containing 3.90 moles of ideal He gas at 26.0°C is placed inside a completely evacuated insulated bell jar of volume 39.0 L .A small hole in the tank allows the He to leak out into the jar until the gas reaches a final equilibrium state with no more leakage. Part A What is the change in entropy of this system due to the leaking of the gas? ■ ΜΕ ΑΣΦ AS = ? J/K Submit Request Answer Part B Is the process reversible or irreversible?arrow_forwardA-E pleasearrow_forwardThree moles of an ideal gas undergo a reversible isothermal compression at 20.0° C. During this compression, 1900 J of work is done on the gas. For related problem-solving tips and strategies, you may want to view a Video Tutor Solution of Entropy change in a free expansion. Part A What is the change of entropy of the gas? ΤΕ ΑΣΦ AS = Submit Request Answer J/Karrow_forward
- 5.97 Block A, with weight 3w, slides down an inclined plane S of slope angle 36.9° at a constant speed while plank B, with weight w, rests on top of A. The plank is attached by a cord to the wall (Fig. P5.97). (a) Draw a diagram of all the forces acting on block A. (b) If the coefficient of kinetic friction is the same between A and B and between S and A, determine its value. Figure P5.97 B A S 36.9°arrow_forwardPlease take your time and solve each part correctly please. Thank you!!arrow_forwardhelp me answer this with explanations! thanks so mucharrow_forward
- No chatgpt pls will upvote Alreadyarrow_forwardWhat fuel economy should be expected from a gasoline powered car that encounters a total of 443N of resistive forces while driving down the road? (Those forces are from air drag, rolling resistance and bearing losses.) Assume a 30% thermodynamic efficiency.arrow_forwardNo chatgpt pls will upvotearrow_forward
- 12. What is the angle between two unit vectors if their dot product is 0.5?arrow_forwardIf the car in the previous problem increases its power output by 10% (by pressing the gas pedal farther down), at what rate will the car accelerate? Hint: Consider the net force. In the previous problem the power was 31.8kWarrow_forwardWhat power is required (at the wheels) for a 1400 kg automobile to climb a 4% grade at a constant speed 30 m/s while it is opposed by drag and rolling resistance forces totaling 500 N?arrow_forward
 Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





