
Concept explainers
Figure 21-18 shows four situations in which particles of charge +q or −q are fixed in place. In each situation, the particles on the x axis are equidistant from the y axis. First, consider the middle particle in situation 1; the middle particle experiences an electrostatic force from each of the other two particles. (a) Are the magnitudes F of those forces the same or different? (b) Is the magnitude of the net force on the middle particle equal to, greater than, or less than 2F? (c) Do the x components of the two forces add or cancel? (d) Do their y components add or cancel? (e) Is the direction of the net force on the middle particle that of the canceling components or the adding components? (f) What is the direction of that net force? Now consider the remaining situations: What is the direction of the net force on the middle particle in (g) situation 2, (h) situation 3, and (i) situation 4? (In each situation, consider the symmetry of the charge distribution and determine the canceling components and the adding components.)
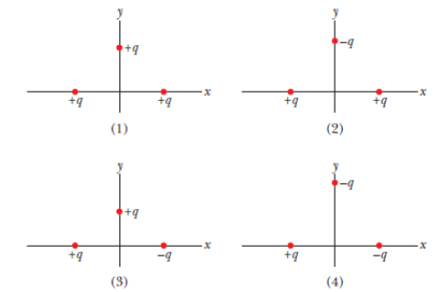
Figure 21-18 Question 9.
Want to see the full answer?
Check out a sample textbook solution
Chapter 21 Solutions
Fundamentals of Physics Extended
Additional Science Textbook Solutions
Physics for Scientists and Engineers: A Strategic Approach, Vol. 1 (Chs 1-21) (4th Edition)
Chemistry & Chemical Reactivity
Microbiology: An Introduction
Microbiology: An Introduction
Campbell Biology (11th Edition)
Fundamentals Of Thermodynamics
- Q: What is the direction of the magnetic field at point A, due to the current I in a wire, in each of the cases 1 to 6 shown below? Note: point A is in the plane of the page. ▪A I I ▪A (1) (2) ▪A • I (out of page) (3) ▪A I x I (into page) ▪A ▪A I (4) (5) (6)arrow_forwardA tennis ball is thrown into the air with initial speed vo=46 m/s and angle (theta) 38 degrees from the ground. Find the distance it travels (x) when it hits the ground.arrow_forwardProblem 04.08 (17 points). Answer the following questions related to the figure below. ථි R₁ www R₂ E R₁ www ли R₁ A Use Kirchhoff's laws to calculate the currents through each battery and resistor in terms of R1, R2, E1, & E2. B Given that all the resistances and EMFs have positive values, if E₁ > E2 and R₁ > R2, which direction is the current flowing through E₁? Through R₂? C If E1 E2 and R₁ > R2, which direction is the current flowing through E₁? Through R2?arrow_forward
- A 105- and a 45.0-Q resistor are connected in parallel. When this combination is connected across a battery, the current delivered by the battery is 0.268 A. When the 45.0-resistor is disconnected, the current from the battery drops to 0.0840 A. Determine (a) the emf and (b) the internal resistance of the battery. 10 R2 R₁ ww R₁ Emf 14 Emf Final circuit Initial circuitarrow_forwardA ball is shot at an angle of 60° with the ground. What should be the initial velocity of the ball so that it will go inside the ring 8 meters away and 3 meters high. Suppose that you want the ball to be scored exactly at the buzzer, determine the required time to throw and shoot the ball. Full solution and figure if there is.arrow_forwardCorrect answer please. I will upvote.arrow_forward
- Define operational amplifierarrow_forwardA bungee jumper plans to bungee jump from a bridge 64.0 m above the ground. He plans to use a uniform elastic cord, tied to a harness around his body, to stop his fall at a point 6.00 m above the water. Model his body as a particle and the cord as having negligible mass and obeying Hooke's law. In a preliminary test he finds that when hanging at rest from a 5.00 m length of the cord, his body weight stretches it by 1.55 m. He will drop from rest at the point where the top end of a longer section of the cord is attached to the bridge. (a) What length of cord should he use? Use subscripts 1 and 2 respectively to represent the 5.00 m test length and the actual jump length. Use Hooke's law F = KAL and the fact that the change in length AL for a given force is proportional the length L (AL = CL), to determine the force constant for the test case and for the jump case. Use conservation of mechanical energy to determine the length of the rope. m (b) What maximum acceleration will he…arrow_forward9 V 300 Ω www 100 Ω 200 Ω www 400 Ω 500 Ω www 600 Ω ww 700 Ω Figure 1: Circuit symbols for a variety of useful circuit elements Problem 04.07 (17 points). Answer the following questions related to the figure below. A What is the equivalent resistance of the network of resistors in the circuit below? B If the battery has an EMF of 9V and is considered as an ideal batter (internal resistance is zero), how much current flows through it in this circuit? C If the 9V EMF battery has an internal resistance of 2 2, would this current be larger or smaller? By how much? D In the ideal battery case, calculate the current through and the voltage across each resistor in the circuit.arrow_forward
- helparrow_forwardIf the block does reach point B, how far up the curved portion of the track does it reach, and if it does not, how far short of point B does the block come to a stop? (Enter your answer in m.)arrow_forwardTruck suspensions often have "helper springs" that engage at high loads. One such arrangement is a leaf spring with a helper coil spring mounted on the axle, as shown in the figure below. When the main leaf spring is compressed by distance yo, the helper spring engages and then helps to support any additional load. Suppose the leaf spring constant is 5.05 × 105 N/m, the helper spring constant is 3.50 × 105 N/m, and y = 0.500 m. Truck body yo Main leaf spring -"Helper" spring Axle (a) What is the compression of the leaf spring for a load of 6.00 × 105 N? Your response differs from the correct answer by more than 10%. Double check your calculations. m (b) How much work is done in compressing the springs? ☑ Your response differs significantly from the correct answer. Rework your solution from the beginning and check each step carefully. Jarrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





