Chapter 2, Problem 25P

Light from a Window A Norman window has the shape of a rectangle surmounted by a semicircle, as shown in the figure to the left. A Norman window with perimeter 30 ft is to be constructed.

1. (a) Find a function that models the area of the window.
2. (b) Find the dimensions of the window that admits the greatest amount of light.

To determine

To find: The function that models the area of the window.

Answer to Problem 25P

The function that models the area of the window is $A\left(x\right)=15x-\left(\frac{\pi +4}{8}\right)x^2$.

Explanation of Solution

Given:

A Norman window is in the shape of the rectangle with perimeter $30\text{ft}$ shown below.

Figure (1)

Formula used:

The area of the rectangle is,

$\text{Area}\text{of}\text{rectangle}=\text{length}\text{×}\text{breadth}$ (1)

Perimeter of the rectangle is,

$\text{Perimeter}\text{of}\text{rectangle}=2\left(\text{length}+\text{breadth}\right)$ (2)

The area of the semi circle is,

$\text{Area}\text{of}\text{semicircle}=\frac{\pi r^2}{2}$ (3)

Perimeter of the semi circle is,

$\text{Perimeter}\text{of}\text{semi circle}=\pi r$ (4)

Calculation:

Let the length in the Norman window is l units and the radius of the semicircle is r units.

The Norman window with the radius of the semicircle and the length of the rectangle is shown below.

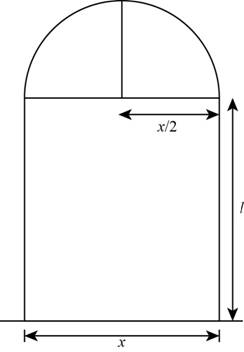
Figure (2)

The radius of the semicircle is,

$r=\frac{x}{2}$

The perimeter of the Norman window is,

$\begin{array}{c}\text{Perimeter of the Norman window}=\text{Perimeter of semicircle}+\text{Perimeter}\text{of}\text{rectangle }\\ 30=\pi r+x+2l\end{array}$

Substitute $\frac{x}{2}$ for r in the above equation,

$\begin{array}{l}30=\frac{\pi x}{2}+x+2l\\ 30=\frac{\pi x+2x+4l}{2}\\ 60=\pi x+2x+4l\\ 4l=60-x\left(\pi +2\right)\end{array}$

Further solve the equation,

$\begin{array}{c}l=\frac{60}{4}-\frac{x\left(\pi +2\right)}{4}\\ =15-\frac{x\left(\pi +2\right)}{4}\end{array}$

The length of the window is $l=15-\frac{x\left(\pi +2\right)}{4}$.

The area of the Norman window is,

$\begin{array}{c}\text{Area of Norman window}=\text{Area of semicircle}+\text{Area}\text{of}\text{rectangle}\\ A\text{=}\frac{\pi r^2}{2}+lx\end{array}$

Substitute $\frac{x}{2}$ for r and $15-\frac{x\left(\pi +2\right)}{4}$ for l in the above equation,

$\begin{array}{c}A\text{=}\frac{\pi {\left(\frac{x}{2}\right)}^2}{2}+\left(15-\frac{x\left(\pi +2\right)}{4}\right)x\\ =\frac{\pi x^2}{8}+15x-\frac{x^2\left(\pi +2\right)}{4}\\ =15x+\frac{\pi x^2-2x^2\pi -4x^2}{8}\\ =15x+\frac{-x^2\pi -4x^2}{8}\end{array}$

Further solve the above equation,

$\begin{array}{c}A\left(x\right)=15x+\frac{-x^2\pi -4x^2}{8}\\ =15x-\frac{\left(\pi +4\right)x^2}{8}\end{array}$

Thus, the function that models the area of the window is $A\left(x\right)=15x-\left(\frac{\pi +4}{8}\right)x^2$.

To determine

To find: The dimension of the window that admits the greatest light.

Answer to Problem 25P

The width of the Norman window is $8.4\text{ft}$ and the length of the Norman window is $4.200\text{ft}$.

Explanation of Solution

From the part(a), the function that models the area of the window is $A\left(x\right)=15x-\left(\frac{\pi +4}{8}\right)x^2$.

To find the dimension that admits the greatest amount of light, it needs to draw the graph of the function $A\left(x\right)=15x-\left(\frac{\pi +4}{8}\right)x^2$.

The function contains the variable x is the breadth of the rectangular portion of the window.

The local maximum value of the function is the maximum finite value where the value of the function at the any number is greater than to the original function.

The condition for local minimum is,

$f\left(a\right)\ge f\left(x\right)$

The graph of the function is shown below,

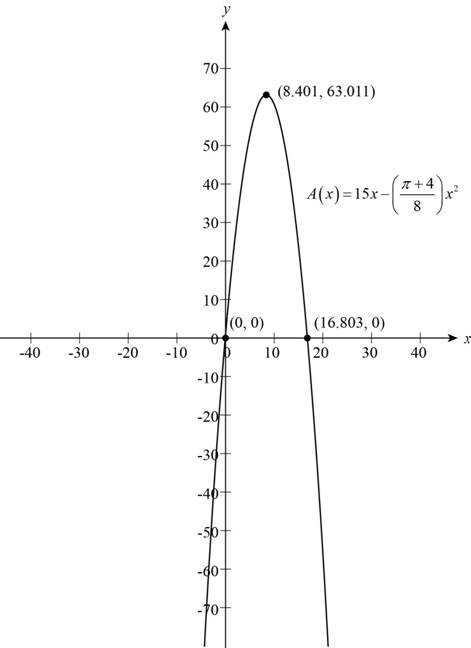
Figure (3)

From the graph of the function shown as Figure (3) the greatest peak of the graph at the point $\left(8.401,63.011\right)$.

Then the maximum light admit from the Norman window is $63.011$ at $x=8.401$.

Substitute 8.4 for x in the length $l=15-\frac{x\left(\pi +2\right)}{4}$,

$\begin{array}{c}l=15-\frac{8.4\left(\frac{22}{7}+2\right)}{4}\\ =15-2.1\left(3.14+2\right)\\ =15-2.1\cdot 5.14\\ =15-10.794=4.2\end{array}$

The length of the window is $4.200\text{ft}$.

Thus, the width of the Norman window is $8.4\text{ft}$ and the length of the Norman window is $4.200\text{ft}$.