
Concept explainers
a.
To graph: the given data on
a.
Answer to Problem 5CFU
Explanation of Solution
Given information:
| Academic year | Average of students per computer |
| 1988-1989 | 25 |
| 1989-1990 | 22 |
| 1990-1991 | 20 |
| 1991-1992 | 18 |
| 1992-1993 | 16 |
| 1993-1994 | 14 |
| 1994-1995 | 10.5 |
| 1995-1996 | 10 |
| 19996-1997 | 7.8 |
| 1997-1998 | 6.1 |
| 1998-1999 | 5.7 |
| 1999-2000 | 5.4 |
| 2000-2001 | 5 |
| 2001-2002 | 4.9 |
| ? | 1 |
Calculation:
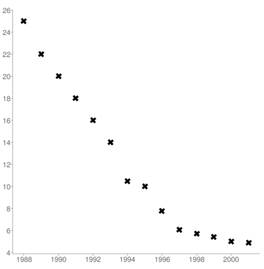
Let the year be x and the average be y. Plot of the graph from the given data will be as follows:
b.
To find: the equation of a best fit line by using two ordered pairs.
b.
Answer to Problem 5CFU
Explanation of Solution
Given information:
| Academic year | Average of students per computer |
| 1988-1989 | 25 |
| 1989-1990 | 22 |
| 1990-1991 | 20 |
| 1991-1992 | 18 |
| 1992-1993 | 16 |
| 1993-1994 | 14 |
| 1994-1995 | 10.5 |
| 1995-1996 | 10 |
| 19996-1997 | 7.8 |
| 1997-1998 | 6.1 |
| 1998-1999 | 5.7 |
| 1999-2000 | 5.4 |
| 2000-2001 | 5 |
| 2001-2002 | 4.9 |
| ? | 1 |
Calculation:
Select any two ordered pairs like
Put any point coordinate and slope value into the slope intercept formula and evaluate the y -intercept as follows:
Now, put the values of slope and b into the slope intercept formula as follows:
Thus, the equation is
c.
To find: the equation of regression line and its
c.
Answer to Problem 5CFU
Explanation of Solution
Given information:
| Academic year | Average of students per computer |
| 1988-1989 | 25 |
| 1989-1990 | 22 |
| 1990-1991 | 20 |
| 1991-1992 | 18 |
| 1992-1993 | 16 |
| 1993-1994 | 14 |
| 1994-1995 | 10.5 |
| 1995-1996 | 10 |
| 19996-1997 | 7.8 |
| 1997-1998 | 6.1 |
| 1998-1999 | 5.7 |
| 1999-2000 | 5.4 |
| 2000-2001 | 5 |
| 2001-2002 | 4.9 |
| ? | 1 |
Calculation:
From the graph
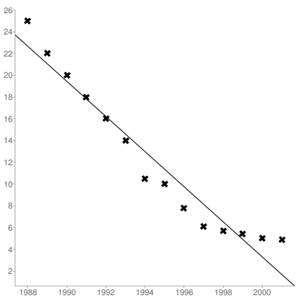
By using the graphing calculator, we get slope value as
Now, put the values in the following equation and evaluate regression of equation of line
Thus, the regression line equation is
By using graphing calculator, the value of
d.
To explain: the whether the relationship predicted by the equation for the missing value is reliable.
d.
Answer to Problem 5CFU
2001
The average number of students cannot be less than 1 student. Thus, the predicted value is the last reliable prediction that can be made with this regression line
Explanation of Solution
Given information:
| Academic year | Average of students per computer |
| 1988-1989 | 25 |
| 1989-1990 | 22 |
| 1990-1991 | 20 |
| 1991-1992 | 18 |
| 1992-1993 | 16 |
| 1993-1994 | 14 |
| 1994-1995 | 10.5 |
| 1995-1996 | 10 |
| 19996-1997 | 7.8 |
| 1997-1998 | 6.1 |
| 1998-1999 | 5.7 |
| 1999-2000 | 5.4 |
| 2000-2001 | 5 |
| 2001-2002 | 4.9 |
| ? | 1 |
Calculation:
Since
Putting the value of
If average number of students shares less than one and greater than zero computer, that means the number of computers are more than students, or multiple computers for all.
It is possible that a school has more computers than students, but it sound unrealistic. Since this is the average data of all US public schools, then there will be more students than computers.
In the years 2001 to 2003, the computer sharing by the average number of students becomes negative. The average number of students cannot be less than 1 student. Thus, the predicted value is the last reliable prediction that can be made with this regression line.
Chapter 1 Solutions
Advanced Mathematical Concepts: Precalculus with Applications, Student Edition
Additional Math Textbook Solutions
University Calculus: Early Transcendentals (4th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Calculus: Early Transcendentals (2nd Edition)
College Algebra with Modeling & Visualization (5th Edition)
- Can you solve this 2 question numerical methodarrow_forward1. Estimate the area under the graph of f(x)-25-x from x=0 to x=5 using 5 approximating rectangles Using: (A) right endpoints. (B) left endpoints.arrow_forward9. Use fundamental theorem of calculus to find the derivative d a) *dt sin(x) b)(x)√1-2 dtarrow_forward
- 3. Evaluate the definite integral: a) √66x²+8dx b) x dx c) f*(2e* - 2)dx d) √√9-x² e) (2-5x)dx f) cos(x)dx 8)²₁₂√4-x2 h) f7dx i) f² 6xdx j) ²₂(4x+3)dxarrow_forward2. Consider the integral √(2x+1)dx (a) Find the Riemann sum for this integral using right endpoints and n-4. (b) Find the Riemann sum for this same integral, using left endpoints and n=4arrow_forward5. For the function y-x³-3x²-1, use derivatives to: (a) determine the intervals of increase and decrease. (b) determine the local (relative) maxima and minima. (e) determine the intervals of concavity. (d) determine the points of inflection. (e) sketch the graph with the above information indicated on the graph.arrow_forward
- Problem 11 (a) A tank is discharging water through an orifice at a depth of T meter below the surface of the water whose area is A m². The following are the values of a for the corresponding values of A: A 1.257 1.390 x 1.50 1.65 1.520 1.650 1.809 1.962 2.123 2.295 2.462|2.650 1.80 1.95 2.10 2.25 2.40 2.55 2.70 2.85 Using the formula -3.0 (0.018)T = dx. calculate T, the time in seconds for the level of the water to drop from 3.0 m to 1.5 m above the orifice. (b) The velocity of a train which starts from rest is given by the fol- lowing table, the time being reckoned in minutes from the start and the speed in km/hour: | † (minutes) |2|4 6 8 10 12 14 16 18 20 v (km/hr) 16 28.8 40 46.4 51.2 32.0 17.6 8 3.2 0 Estimate approximately the total distance ran in 20 minutes.arrow_forwardX Solve numerically: = 0,95 In xarrow_forwardX Solve numerically: = 0,95 In xarrow_forward
- Please as many detarrow_forward8–23. Sketching vector fields Sketch the following vector fieldsarrow_forward25-30. Normal and tangential components For the vector field F and curve C, complete the following: a. Determine the points (if any) along the curve C at which the vector field F is tangent to C. b. Determine the points (if any) along the curve C at which the vector field F is normal to C. c. Sketch C and a few representative vectors of F on C. 25. F = (2½³, 0); c = {(x, y); y − x² = 1} 26. F = x (23 - 212) ; C = {(x, y); y = x² = 1}) , 2 27. F(x, y); C = {(x, y): x² + y² = 4} 28. F = (y, x); C = {(x, y): x² + y² = 1} 29. F = (x, y); C = 30. F = (y, x); C = {(x, y): x = 1} {(x, y): x² + y² = 1}arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





