
For the circuit in Fig. 15.55, (a) derive an algebraic expression for the transfer function H(jω) = iout/vin in terms of circuit components R1, R2, L1, and L2; (b) evaluate the the magnitude of H(jω) at frequencies of 10 kHz, 1 MHz, and 100 MHz for the case where R1 = 3 kΩ, R2 = 12 kΩ, L1 = 5 mH, and L2 = 8 mH; (c) qualitatively, explain the behavior of the transfer function magnitude frequency response.
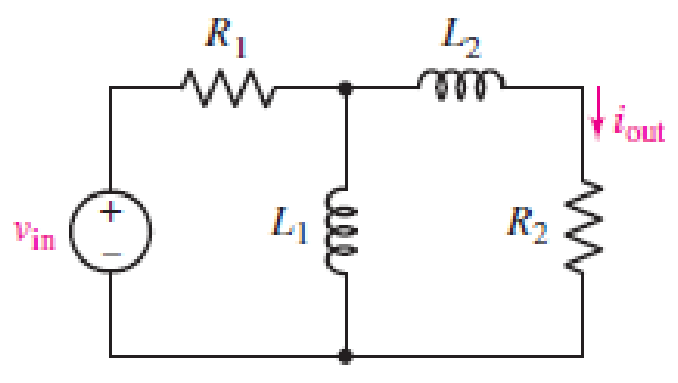
■ FIGURE 15.55
(a)
Find an algebraic expression for the transfer function
Answer to Problem 5E
The transfer function
Explanation of Solution
Given data:
Refer to Figure 15.55 in the textbook.
Formula used:
Write the expression to calculate the impedance of the passive elements resistor and inductor.
Here,
Calculation:
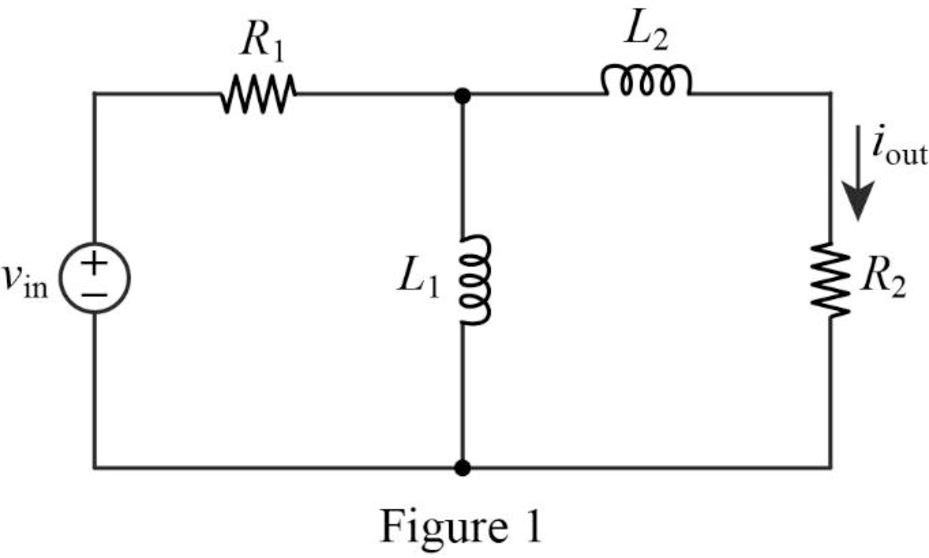
The given circuit is redrawn as Figure 1.
The impedance circuit of the Figure 1 is drawn as Figure 2 using the equations (1) and (2).
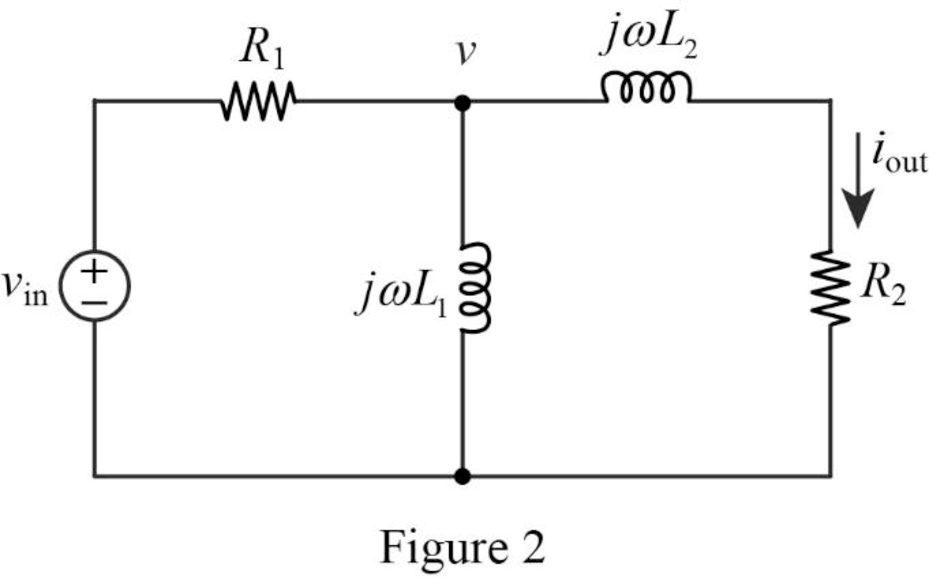
Write the general expression to calculate the transfer function of the circuit in Figure 2.
Here,
Use nodal analysis on node
Rearrange the above equation to find
The output current
Substitute
Simplify the above equation to find
Substitute
Conclusion:
Thus, the transfer function
(b)
Find the value of magnitude of
Answer to Problem 5E
The value of magnitude of the transfer function
Explanation of Solution
Given data:
The value of the resistor 1
The value of the resistor 2
The value of the inductor 1
The value of the inductor 2
Formula used:
Write the expression to calculate the angular frequency.
Here,
Calculation:
From part (a), the transfer function is,
Substitute
Substitute
For frequency of 10 kHz:
Substitute
Take magnitude for above equation to find
For frequency of 1 MHz:
Substitute
Take magnitude for above equation to find
For frequency of 100 MHz:
Substitute
Take magnitude for above equation to find
Conclusion:
Thus, the value of magnitude of the transfer function
(c)
Explain the behavior of the transfer function magnitude frequency response.
Explanation of Solution
Discussion:
At lower frequencies
It is clear that the current
The magnitude approaches zero at low and high frequencies and at medium frequencies, the magnitude approaches maximum value. It implies the characteristics of the band-pass filter.
Conclusion:
Thus, the behavior of the transfer function magnitude frequency response is explained.
Want to see more full solutions like this?
Chapter 15 Solutions
Engineering Circuit Analysis
Additional Engineering Textbook Solutions
Electric Circuits. (11th Edition)
Fluid Mechanics: Fundamentals and Applications
Problem Solving with C++ (10th Edition)
Starting Out with Programming Logic and Design (5th Edition) (What's New in Computer Science)
Java: An Introduction to Problem Solving and Programming (8th Edition)
Starting Out with Java: From Control Structures through Objects (7th Edition) (What's New in Computer Science)
- Solve in detail to understandarrow_forwardPlease solve in detailarrow_forward6.7 The transmitting aerial shown in Fig. Q.3 is supplied with current at 80 A peak and at frequency 666.66 kHz. Calculate (a) the effective height of the aerial, and (b) the electric field strength produced at ground level 40 km away. 60 m Fig. Q.3 Input 48 m Eartharrow_forward
- ox SIM 12.11 Consider the class B output stage, using MOSFETs, shown in Fig. P12.11. Let the devices have |V|= 0.5 V and μC WIL = 2 mA/V². With a 10-kHz sine-wave input of 5-V peak and a high value of load resistance, what peak output would you expect? What fraction of the sine-wave period does the crossover interval represent? For what value of load resistor is the peak output voltage reduced to half the input? Figure P12.11 +5 V Q1 Q2 -5Varrow_forward4 H ་་་་་་་ 四一周 A H₂ Find out put c I writ R as a function G, H, Harrow_forward4 H A H₂ 四一周 Find out put c I writ R as a function G, H, Harrow_forward
- 8. (a) In a Round-Robin tournament, the Tigers beat the Blue Jays, the Tigers beat the Cardinals, the Tigers beat the Orioles, the Blue Jays beat the Cardinals, the Blue Jays beat the Orioles and the Cardinals beat the Orioles. Model this outcome with a directed graph. https://www.akubihar.com (b) (c) ✓ - Let G = (V, E) be a simple graph. Let R be the relation on V consisting of pairs of vertices (u, v) such that there is a path from u to vor such that u= v. Show that R is an equivalence relation. 3 3 Determine whether the following given pair of directed graphs, shown in Fig. 1 and Fig. 2, are isomorphic or not. Exhibit an isomorphism or provide a rigorous argument that none exists. 4+4=8 Աշ աշ ИНИЯ Fig. 1 Fig. 2 Querarrow_forwardEXAMPLE 4.5 Objective: Determine ID, circuit. V SG' SD Vs and the small - signal voltage gain of a PMOS transistor Consider the circuit shown in Figure 4.20(a). The transistor parameters are A K = 0.80m- V Р _2’TP = 0.5V, and λ = 0 Varrow_forwardNeed a solution and don't use chatgptarrow_forward
- Need a solarrow_forwardDo not use chaarrow_forwardIn the following table, the value of 40 resistors are recorded in ohms. (a) Construct the frequency distribution table using number of class=5. (b) Plot the histogram of frequency table. 45 50 61 32 25 50 64 28 40 40 46 47 48 35 58 35 54 38 68 76 19 63 26 65 54 42 68 47 53 36 73 44 49 35 38 42 56 44 45 57arrow_forward
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,





