Chapter 15, Problem 16E

(a)

To determine

Find the value of $\xi$ and ${\omega }_0$ in terms of $R$, $L$ and $C$ for the series RLC circuit.

Answer to Problem 16E

The value of $\xi$ and ${\omega }_0$ in terms of $R$, $L$ and $C$ for the circuit in Figure 1 is $\frac{R}{2}\sqrt{\frac{C}{L}}$ and $\frac{1}{\sqrt{LC}}$ respectively.

Explanation of Solution

Given data:

Refer to Figure 15.53 in the textbook.

Formula used:

Write the expression to calculate the impedance of the passive elements resistor, inductor and capacitor in s-domain.

$Z_R=R$        (1)

$Z_L=sL$        (2)

$Z_C=\frac{1}{sC}$        (3)

Here,

$\omega$ is the angular frequency,

$R$ is the value of the resistor,

$L$ is the value of the inductor, and

$C$ is the value of the capacitor.

Calculation:

Given that the output voltage should be taken across the inductor in series RLC circuit.

Generally, the transfer function of the series RLC circuit for which the output is taken across the inductor is,

$H\left(s\right)=\frac{v_L}{v_{\text{in}}}=\frac{{\left(\frac{s}{{\omega }_0}\right)}^2}{1+2\xi \left(\frac{s}{{\omega }_0}\right)+{\left(\frac{s}{{\omega }_0}\right)}^2}$        (4)

The modified circuit of given circuit is drawn as Figure 1.

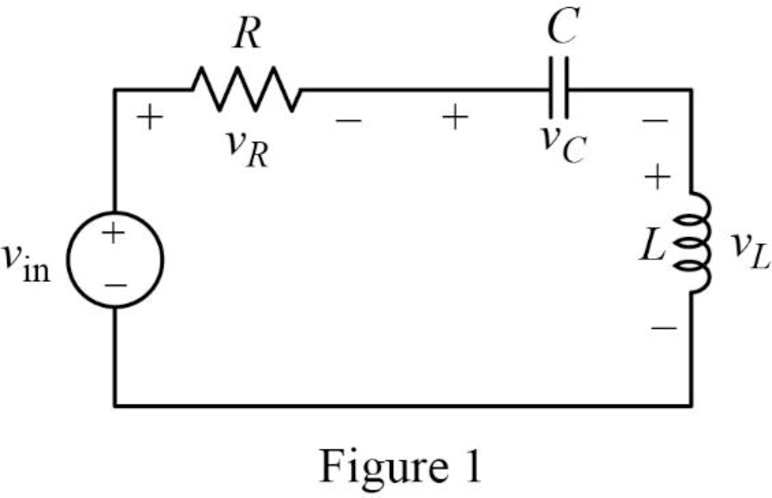
The Figure 1 is redrawn as impedance circuit in s-domain in Figure 2 using the equations (1), (2) and (3).

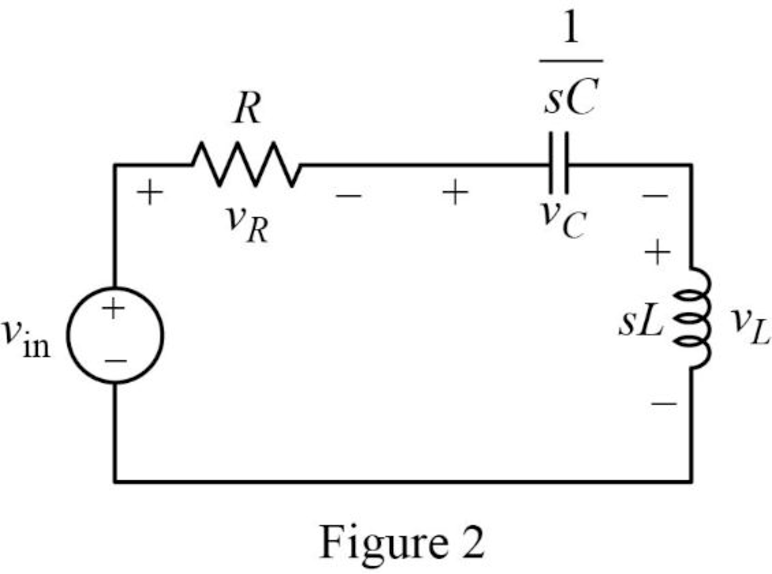
Write the general expression to calculate the transfer function of the circuit in Figure 2.

$H\left(s\right)=\frac{v_L}{v_{\text{in}}}$        (5)

Here,

$v_L$ is the output response of the system, and

$v_{\text{in}}$ is the input response of the system.

Apply Kirchhoff’s voltage law on Figure 2 to find $v_L$.

$\begin{array}{c}{v}_L=\frac{sL}{\left(R+sL+\frac{1}{sC}\right)}{v}_{\text{in}}\\ =\frac{sL}{\left(\frac{sRC+s^{2}LC+1}{sC}\right)}{v}_{\text{in}}\\ =\frac{LC{s}^2}{1+RCs+LC{s}^2}{v}_{\text{in}}\end{array}$

Rearrange the above equation to find $\frac{v_L}{v_{\text{in}}}$.

$\frac{v_L}{v_{\text{in}}}=\frac{LC{s}^2}{1+RCs+LC{s}^2}$

Substitute $\frac{LC{s}^2}{1+RCs+LC{s}^2}$ for $\frac{v_L}{v_{\text{in}}}$ in equation (5) to find $H\left(s\right)$.

$H\left(s\right)=\frac{LC{s}^2}{1+RCs+LC{s}^2}$

Compare the above equation with the equation (4) to obtain the following values.

$LC={\left(\frac{1}{{\omega }_0}\right)}^2$        (6)

$RC=\frac{2\xi }{{\omega }_0}$        (7)

Rearrange the equation (6).

$\sqrt{LC}=\frac{1}{{\omega }_0}$

Rearrange the above equation to find ${\omega }_0$.

${\omega }_0=\frac{1}{\sqrt{LC}}$

Rearrange the equation (7) to find $\xi$.

$\xi =\frac{RC{\omega }_0}{2}$

Substitute $\frac{1}{\sqrt{LC}}$ for ${\omega }_0$ in above equation to find $\xi$.

$\begin{array}{c}\xi =\frac{RC}{2\sqrt{LC}}\\ =\frac{R\sqrt{C}\sqrt{C}}{2\sqrt{L}\sqrt{C}}\\ =\frac{R\sqrt{C}}{2\sqrt{L}}\\ =\frac{R}{2}\sqrt{\frac{C}{L}}\end{array}$

Conclusion:

Thus, the value of $\xi$ and ${\omega }_0$ in terms of $R$, $L$ and $C$ for the circuit in Figure 1 is $\frac{R}{2}\sqrt{\frac{C}{L}}$ and $\frac{1}{\sqrt{LC}}$ respectively.

(b)

To determine

Find the values of inductor $\left(L\right)$ and capacitor $\left(C\right)$ to achieve ${\omega }_0$ of $5\times {10}^3\frac{\text{rad}}{\text{s}}$ and three cases of $\xi =0.1,0.5\text{and}1$.

Answer to Problem 16E

The value of inductor $\left(L\right)$ and capacitor $\left(C\right)$ to achieve ${\omega }_0$ of $5\times {10}^3\frac{\text{rad}}{\text{s}}$ at $\xi =0.1,0.5\text{and}1$ is $100\text{mH}$ and $400\text{nF}$, $20\text{mH}$ and $2\mu \text{F}$, $10\text{mH}$ and $4\mu \text{F}$ respectively.

Explanation of Solution

Given data:

The value of the resistor $\left(R\right)$ is $100\Omega$.

The value of the resonant frequency $\left({\omega }_0\right)$ is $5\times {10}^3\frac{\text{rad}}{\text{s}}$.

Calculation:

Case (i): $\xi =0.1$

From part (a),

$\xi =\frac{R}{2}\sqrt{\frac{C}{L}}$        (8)

${\omega }_0=\frac{1}{\sqrt{LC}}$        (9)

Substitute $0.1$ for $\xi$ and $100\Omega$ for $R$ in equation (8).

$\begin{array}{l}0.1=\frac{100}{2}\sqrt{\frac{C}{L}}\\ 0.1=50\sqrt{\frac{C}{L}}\end{array}$

Rearrange the above equation to find $\frac{C}{L}$.

$\begin{array}{c}\frac{C}{L}={\left(\frac{0.1}{50}\right)}^2\\ =4\times {10}^{-6}\end{array}$

Rearrange the above equation to find $C$.

$C=\left(4\times {10}^{-6}\right)L$        (10)

Rearrange the equation (9).

${\omega }_0{}^2=\frac{1}{LC}$

Rearrange the above equation to find $LC$.

$LC=\frac{1}{{\omega }_0{}^2}$        (11)

Substitute $\left(4\times {10}^{-6}\right)L$ for $C$ and $5\times {10}^3\frac{\text{rad}}{\text{s}}$ for ${\omega }_0$ in equation (11).

$\begin{array}{l}L\left(\left(4\times {10}^{-6}\right)L\right)=\frac{1}{{\left(5\times {10}^3\frac{\text{rad}}{\text{s}}\right)}^2}\\ \left(4\times {10}^{-6}\right)L^2=\frac{1}{\left(25\times {10}^6\right)}\end{array}$

Rearrange the above equation to find $L^2$.

$\begin{array}{c}{L}^2=\frac{1}{\left(25\times {10}^6\right)\left(4\times {10}^{-6}\right)}\\ =\frac{1}{100}\end{array}$

Take square root on both sides of the above equation to find $L$.

$\begin{array}{l}\sqrt{L^2}=\sqrt{\frac{1}{100}}\\ L=100\times {10}^{-3}\text{H}\\ L=100\text{mH}\left\{\because 1\text{m}={10}^{-3}\right\}\end{array}$

Substitute $100\times {10}^{-3}\text{H}$ for $L$ in equation (10) to find $C$.

$\begin{array}{c}C=\left(4\times {10}^{-6}\right)\left(100\times {10}^{-3}\right)\\ =\left(400\times {10}^{-9}\right)\text{F}\\ =400\text{nF}\left\{\because 1\text{n}={10}^{-9}\right\}\end{array}$

Case (ii): $\xi =0.5$

Substitute $0.5$ for $\xi$ and $100\Omega$ for $R$ in equation (8).

$\begin{array}{l}0.5=\frac{100}{2}\sqrt{\frac{C}{L}}\\ 0.5=50\sqrt{\frac{C}{L}}\end{array}$

Rearrange the above equation to find $\frac{C}{L}$.

$\begin{array}{c}\frac{C}{L}={\left(\frac{0.5}{50}\right)}^2\\ =1\times {10}^{-4}\end{array}$

Rearrange the above equation to find $C$.

$C=\left(1\times {10}^{-4}\right)L$        (12)

Substitute $\left(1\times {10}^{-4}\right)L$ for $C$ and $5\times {10}^3\frac{\text{rad}}{\text{s}}$ for ${\omega }_0$ in equation (11).

$\begin{array}{l}L\left(\left(1\times {10}^{-4}\right)L\right)=\frac{1}{{\left(5\times {10}^3\frac{\text{rad}}{\text{s}}\right)}^2}\\ \left(1\times {10}^{-4}\right)L^2=\frac{1}{\left(25\times {10}^6\right)}\end{array}$

Rearrange the above equation to find $L^2$.

$\begin{array}{c}{L}^2=\frac{1}{\left(25\times {10}^6\right)\left(1\times {10}^{-4}\right)}\\ =\frac{1}{2500}\end{array}$

Take square root on both sides of the above equation to find $L$.

$\begin{array}{c}\sqrt{L^2}=\sqrt{\frac{1}{2500}}\\ L=20\times {10}^{-3}\text{H}\\ =20\text{mH}\left\{\because 1\text{m}={10}^{-3}\right\}\end{array}$

Substitute $20\times {10}^{-3}\text{H}$ for $L$ in equation (12) to find $C$.

$\begin{array}{c}C=\left(1\times {10}^{-4}\right)\left(20\times {10}^{-3}\right)\\ =\left(2\times {10}^{-6}\right)\text{F}\\ =2\mu \text{F}\left\{\because 1\mu ={10}^{-6}\right\}\end{array}$

Case (iii): $\xi =1$

Substitute $1$ for $\xi$ and $100\Omega$ for $R$ in equation (8).

$\begin{array}{l}1=\frac{100}{2}\sqrt{\frac{C}{L}}\\ 1=50\sqrt{\frac{C}{L}}\end{array}$

Rearrange the above equation to find $\frac{C}{L}$.

$\begin{array}{c}\frac{C}{L}={\left(\frac{1}{50}\right)}^2\\ =4\times {10}^{-4}\end{array}$

Rearrange the above equation to find $C$.

$C=\left(4\times {10}^{-4}\right)L$        (13)

Substitute $\left(4\times {10}^{-4}\right)L$ for $C$ and $5\times {10}^3\frac{\text{rad}}{\text{s}}$ for ${\omega }_0$ in equation (11).

$\begin{array}{l}L\left(\left(4\times {10}^{-4}\right)L\right)=\frac{1}{{\left(5\times {10}^3\frac{\text{rad}}{\text{s}}\right)}^2}\\ \left(4\times {10}^{-4}\right)L^2=\frac{1}{\left(25\times {10}^6\right)}\end{array}$

Rearrange the above equation to find $L^2$.

$\begin{array}{c}{L}^2=\frac{1}{\left(25\times {10}^6\right)\left(4\times {10}^{-4}\right)}\\ =\frac{1}{10000}\end{array}$

Take square root on both sides of the above equation to find $L$.

$\begin{array}{c}\sqrt{L^2}=\sqrt{\frac{1}{10000}}\\ L=10\times {10}^{-3}\text{H}\\ =10\text{mH}\left\{\because 1\text{m}={10}^{-3}\right\}\end{array}$

Substitute $10\times {10}^{-3}\text{H}$ for $L$ in equation (13) to find $C$.

$\begin{array}{c}C=\left(4\times {10}^{-4}\right)\left(10\times {10}^{-3}\right)\\ =\left(4\times {10}^{-6}\right)\text{F}\\ =4\mu \text{F}\left\{\because 1\mu ={10}^{-6}\right\}\end{array}$

Conclusion:

Thus, the value of inductor $\left(L\right)$ and capacitor $\left(C\right)$ to achieve ${\omega }_0$ of $5\times {10}^3\frac{\text{rad}}{\text{s}}$ at $\xi =0.1,0.5\text{and}1$ is $100\text{mH}$ and $400\text{nF}$, $20\text{mH}$ and $2\mu \text{F}$, $10\text{mH}$ and $4\mu \text{F}$ respectively.

(c)

To determine

Construct the magnitude Bode plots for the three cases $\xi =0.1,0.5\text{and}1$ using MATLAB.

Explanation of Solution

Calculation:

Simplify the equation (4) to find $H\left(s\right)$.

$\begin{array}{c}H\left(s\right)=\frac{{\left(\frac{s}{{\omega }_0}\right)}^2}{1+2\xi \left(\frac{s}{{\omega }_0}\right)+{\left(\frac{s}{{\omega }_0}\right)}^2}\\ =\frac{\left(\frac{1}{{\omega }_0{}^2}\right)s^2}{\left(\frac{{\omega }_0{}^2+2\xi {\omega }_{0}s+s^2}{{\omega }_0{}^2}\right)}\\ =\frac{\left(\frac{{\omega }_0{}^2}{{\omega }_0{}^2}\right)s^2}{s^2+2\xi {\omega }_{0}s+{\omega }_0{}^2}\end{array}$

$H\left(s\right)=\frac{s^2}{s^2+2\xi {\omega }_{0}s+{\omega }_0{}^2}$        (14)

Case (i): $\xi =0.1$

Substitute $0.1$ for $\xi$ and $5\times {10}^3\frac{\text{rad}}{\text{s}}$ for ${\omega }_0$ in equation (14) to find $H\left(s\right)$.

$H\left(s\right)=\frac{s^2}{s^2+2\left(0.1\right)\left(5\times {10}^3\right)s+{\left(5\times {10}^3\right)}^2}$

$H\left(s\right)=\frac{s^2}{s^2+1000s+\left(25\times {10}^6\right)}$        (15)

Case (ii): $\xi =0.5$

Substitute $0.5$ for $\xi$ and $5\times {10}^3\frac{\text{rad}}{\text{s}}$ for ${\omega }_0$ in equation (14) to find $H\left(s\right)$.

$H\left(s\right)=\frac{s^2}{s^2+2\left(0.5\right)\left(5\times {10}^3\right)s+{\left(5\times {10}^3\right)}^2}$

$H\left(s\right)=\frac{s^2}{s^2+5000s+\left(25\times {10}^6\right)}$        (16)

Case (iii): $\xi =1$

Substitute $1$ for $\xi$ and $5\times {10}^3\frac{\text{rad}}{\text{s}}$ for ${\omega }_0$ in equation (14) to find $H\left(s\right)$.

$H\left(s\right)=\frac{s^2}{s^2+2\left(1\right)\left(5\times {10}^3\right)s+{\left(5\times {10}^3\right)}^2}$

$H\left(s\right)=\frac{s^2}{s^2+10000s+\left(25\times {10}^6\right)}$        (17)

The equations (15), (16) and (17) are the transfer function of the given series RLC circuit at three different cases $\xi =0.1,0.5\text{and}1$.

The MATLAB code is given below to sketch the magnitude Bode plots for the three cases using the equations (15), (16) and (17).

MATLAB Code:

clc;

clear all;

close all;

sys1=tf([1 0 0],[1 1000 (25*10^6)]);

sys2=tf([1 0 0],[1 5000 (25*10^6)]);

sys3=tf([1 0 0],[1 10000 (25*10^6)]);

bode(sys1,sys2,sys3)

legend({'sys1','sys2','sys3'},'Location','best')

Output:

The MATLAB output is shown in Figure 3.

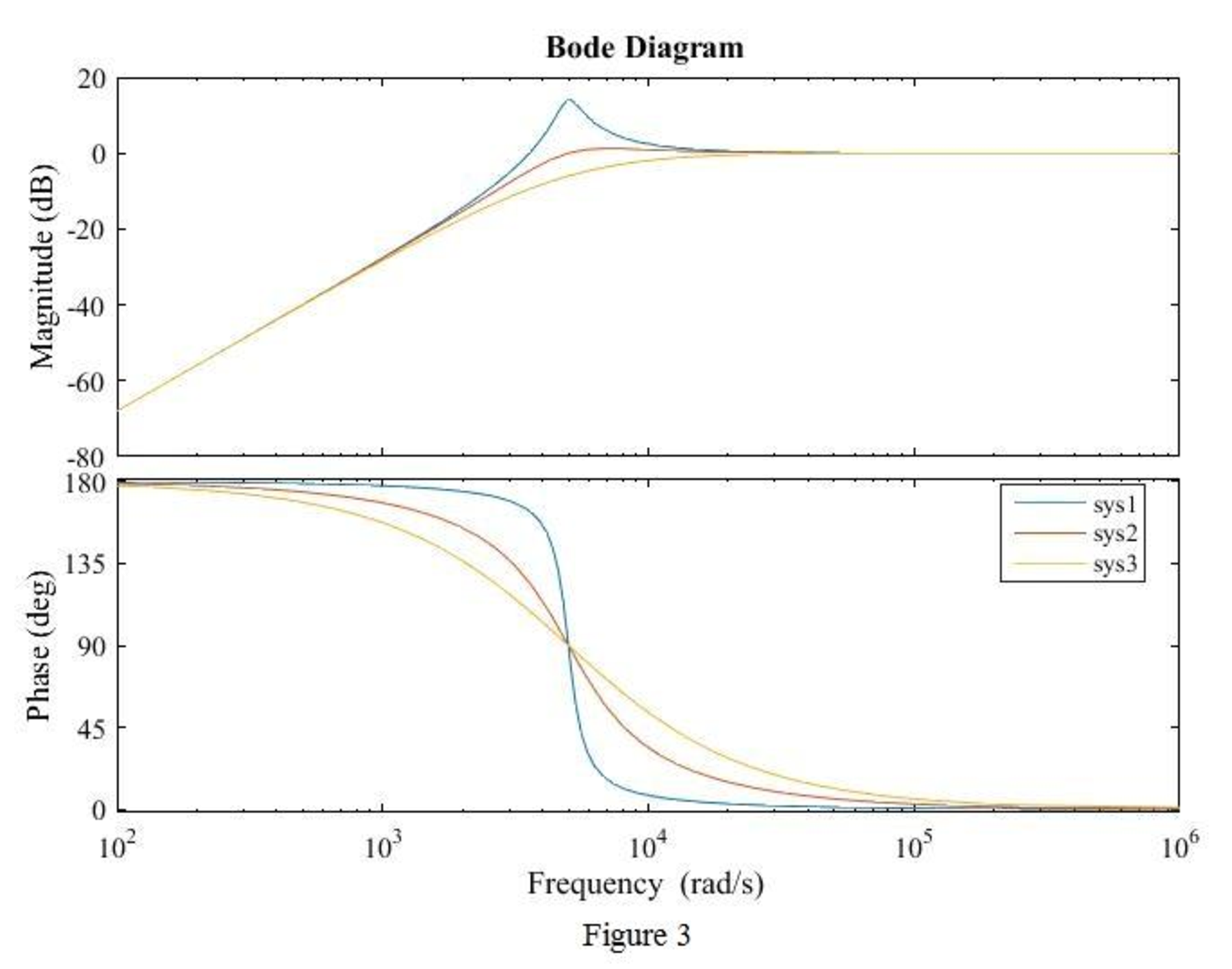
Conclusion:

Thus, the magnitude Bode plot for the three cases $\xi =0.1,0.5\text{and}1$ is constructed using MATLAB.