
Concept explainers
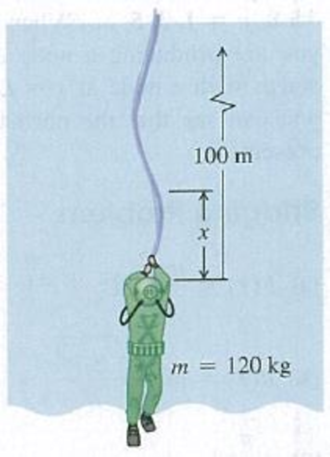
CP CALC A deep-sea diver is suspended beneath the surface of Loch Ness by a 100-m-long cable that is attached to a boat on the surface (Fig. P15.77). The diver and his suit have a total mass of 120 kg and a volume of 0.0800 m3. The cable has a diameter of 2.00 cm and a linear mass density of μ = 1.10 kg/m. The diver thinks he sees something moving in the murky depths and jerks the end of the cable back and forth to send transverse waves up the cable as a signal to his companions in the boat. (a) What is the tension in the cable at its lower end, where it is attached to the diver? Do not forget to include the buoyant force that the water (density 1000 kg/m3) exerts on him. (b) Calculate the tension in the cable a distance x above the diver. In your calculation, include the buoyant force on the cable. (c) The speed of transverse waves on the cable is given by
Want to see the full answer?
Check out a sample textbook solution
Chapter 15 Solutions
University Physics with Modern Physics Plus Mastering Physics with eText -- Access Card Package (14th Edition)
Additional Science Textbook Solutions
Organic Chemistry (8th Edition)
Human Biology: Concepts and Current Issues (8th Edition)
Genetic Analysis: An Integrated Approach (3rd Edition)
Campbell Biology (11th Edition)
Introductory Chemistry (6th Edition)
Biology: Life on Earth (11th Edition)
- An outfielder throws a baseball to his catcher in an attempt to throw out a runner at home plate. The ball bounces once before reaching the catcher. Assume the angle at which the bounced ball leaves the ground is the same as the angle at which the outfielder threw it as shown in the figure, but that the ball's speed after the bounce is one-half of what it was before the bounce. 8 (a) Assuming the ball is always thrown with the same initial speed, at what angle & should the fielder throw the ball to make it go the same distance D with one bounce (blue path) as a ball thrown upward at 35.0° with no bounce (green path)? 24 (b) Determine the ratio of the time interval for the one-bounce throw to the flight time for the no-bounce throw. Cone-bounce no-bounce 0.940arrow_forwardA rocket is launched at an angle of 60.0° above the horizontal with an initial speed of 97 m/s. The rocket moves for 3.00 s along its initial line of motion with an acceleration of 28.0 m/s². At this time, its engines fail and the rocket proceeds to move as a projectile. (a) Find the maximum altitude reached by the rocket. 1445.46 Your response differs from the correct answer by more than 10%. Double check your calculations. m (b) Find its total time of flight. 36.16 x Your response is within 10% of the correct value. This may be due to roundoff error, or you could have a mistake in your calculation. Carry out all intermediate results to at least four-digit accuracy to minimize roundoff error. s (c) Find its horizontal range. 1753.12 × Your response differs from the correct answer by more than 10%. Double check your calculations. marrow_forwardRace car driver is cruising down the street at a constant speed of 28.9 m/s (~65 mph; he has a “lead” foot) when the traffic light in front of him turns red. a) If the driver’s reaction time is 160 ms, how far does he and his car travel down the road from the instant he sees the light change to the instant he begins to slow down? b) If the driver’s combined reaction and movement time is 750 ms, how far do he and his car travel down the road from the instant he sees the light change to the instant he slams on her brakes and car begins to slow down? Please answer parts a-B. Show all work. For each question draw a diagram to show the vector/s. Show all the step and provide units in the answers. Provide answer to 2 decimal places. DONT FORGET TO DRAW VECTORS! ONLY USE BASIC FORMULAS TAUGHT IN PHYSICS. distance = speed * time.arrow_forward
- Race car driver is cruising down the street at a constant speed of 28.9 m/s (~65 mph; he has a “lead” foot) when the traffic light in front of him turns red. a) If the driver’s reaction time is 160 ms, how far does he and his car travel down the road from the instant he sees the light change to the instant he begins to slow down? b) If the driver’s combined reaction and movement time is 750 ms, how far do he and his car travel down the road from the instant he sees the light change to the instant he slams on her brakes and car begins to slow down? c) If the driver’s average rate of acceleration is -9.5 m/s2 as he slows down, how long does it take him to come to a stop (use information about his speed of 28.9 m/s but do NOT use his reaction and movement time in this computation)? Please answer parts a-c. Show all work. For each question draw a diagram to show the vector/s. Show all the step and provide units in the answers. Provide answer to 2 decimal places unless stated otherwise.…arrow_forwardHow is it that part a is connected to part b? I can't seem to solve either part and don't see the connection between the two.arrow_forwardHello, please help with inputing trial one into the equation, I just need a model for the first one so I can answer the rest. Also, does my data have the correct sigfig? Thanks!arrow_forward
- Find the current in the R₁ resistor in the drawing (V₁=16.0V, V2=23.0 V, V₂ = 16.0V, R₁ = 2005, R₂ = and R₂ = 2.705) 2.3052 VIT A www R www R₂ R₂ Vaarrow_forwardWhich of the following laws is true regarding tensile strength? • tensile strength T ①Fbreak = Wtfest Piece thickness rate (mm) ②T = test piece width rabe (mm) Fbreak break watarrow_forwardThe position of a squirrel running in a park is given by = [(0.280 m/s)t + (0.0360 m/s²)t²] + (0.0190 m/s³)ť³ĵj. What is v₂(t), the x-component of the velocity of the squirrel, as a function of time?arrow_forward
 Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning
An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





