
Concept explainers
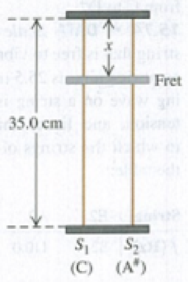
Music. You are designing a two-string instrument with metal strings 35.0 cm long, as shown in Fig. P15.54. Both strings are under the same tension. String S1 has a mass of 8.00 g and produces the note middle C (frequency 262 Hz) in its fundamental mode. 35.0 cm (a) What should be the tension in the string? (b) What should be the mass of string S2 so that it will produce A-sharp (frequency 466 Hz) as its fundamental? (c) To extend the range of your instrument, you include a fret located just under the strings but not normally touching them. How far from the upper end should you put this fret so that when you press S1 tightly against it, this string will produce C-sharp (frequency 277 Hz) in its fundamental? That is, what is x in the figure? (d) If you press S2 against the fret, what frequency of sound will it produce in its fundamental?
Figure P15.54
Want to see the full answer?
Check out a sample textbook solution
Chapter 15 Solutions
University Physics with Modern Physics Plus Mastering Physics with eText -- Access Card Package (14th Edition)
Additional Science Textbook Solutions
Physics (5th Edition)
Essential University Physics: Volume 1 (3rd Edition)
An Introduction to Thermal Physics
University Physics Volume 2
Essential University Physics (3rd Edition)
- The equation of a harmonic wave propagating along a stretched string is represented by y(x, t) = 4.0 sin (1.5x 45t), where x and y are in meters and the time t is in seconds. a. In what direction is the wave propagating? be. N What are the b. amplitude, c. wavelength, d. frequency, and e. propagation speed of the wave?arrow_forwardAt t = 0, a transverse pulse in a wire is described by the function y=6.00x2+3.00 where xand y are in meters. If the pulse is traveling in the positive x direction with a speed of 4.50 m/s, write the function y(x, t) that describes this pulse.arrow_forwardA string with a mass m = 8.00 g and a length L = 5.00 m has one end attached to a wall; the other end is draped over a small, fixed pulley a distance d = 4.00 m from the wall and attached to a hanging object with a mass M = 4.00 kg as in Figure P14.21. If the horizontal part of the string is plucked, what is the fundamental frequency of its vibration? Figure P14.21arrow_forward
- As in Figure P18.16, a simple harmonic oscillator is attached to a rope of linear mass density 5.4 102 kg/m, creating a standing transverse wave. There is a 3.6-kg block hanging from the other end of the rope over a pulley. The oscillator has an angular frequency of 43.2 rad/s and an amplitude of 24.6 cm. a. What is the distance between adjacent nodes? b. If the angular frequency of the oscillator doubles, what happens to the distance between adjacent nodes? c. If the mass of the block is doubled instead, what happens to the distance between adjacent nodes? d. If the amplitude of the oscillator is doubled, what happens to the distance between adjacent nodes? FIGURE P18.16arrow_forwardA pipe is observed to have a fundamental frequency of 345 Hz. Assume the pipe is filled with air (v = 343 m/s). What is the length of the pipe if the pipe is a. closed at one end and b. open at both ends?arrow_forwardA flute has a length of 58.0 cm. If the speed of sound in air is 343 m/s, what is the fundamental frequency of the flute, assuming it is a tube closed at one end and open at the other? (a) 148 Hz (b) 296 Hz (c) 444 Hz (d) 591 Hz (e) none of those answersarrow_forward
- A standing wave on a string is described by the equation y(x, t) = 1.25 sin(0.0350x) cos(1450t), where x is in centimeters, t is in seconds, and the resulting amplitude is in millimeters. a. What is the length of the string if this standing wave represents the first harmonic vibration of the string? b. What is the speed of the wave on this string?arrow_forwardReview. A sphere of mass M is supported by a string that passes over a pulley at the end of a horizontal rod of length L (Fig. P14.25). The string makes an angle θ with the rod. The fundamental frequency of standing waves in the portion of the string above the rod is f. Find the mass of the portion of the string above the rod. Figure P14.25 Problems 25 and 26.arrow_forwardThe bulk modulus of water is 2.2 109 Pa (Table 15.2). The density of water is 103 kg/m3 (Table 15.1). Find the speed of sound in water and compare your answer with the value given in Table 17.1.arrow_forward
- By what factor would you have to multiply the tension in a stretched string so as to double the wave speed? Assume the string does not stretch. (a) a factor of 8 (b) a factor of 4 (c) a factor of 2 (d) a factor of 0.5 (e) You could not change the speed by a predictable factor by changing the tension.arrow_forwardA sound wave in air has a pressure amplitude equal to 4.00 103 Pa. Calculate the displacement amplitude of the wave at a frequency of 10.0 kHz.arrow_forwardA tuning fork is known to vibrate with frequency 262 Hz. When it is sounded along with a mandolin siring, four beats are heard every second. Next, a bit of tape is put onto each line of the tuning fork, and the tuning fork now produces five beats per second with the same mandolin siring. What is the frequency of the string? (a) 257 Hz (b) 258 Hz (c) 262 Hz (d) 266 Hz (e) 267 Hzarrow_forward
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





