McDougal Littell Jurgensen Geometry: Student Edition Geometry
5th Edition
ISBN: 9780395977279
Author: Ray C. Jurgensen, Richard G. Brown, John W. Jurgensen
Publisher: Houghton Mifflin Company College Division
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 14.8, Problem 29WE
a.
To determine
To write the number of planes of symmetry and the number of axes of the rotation the
a.
Expert Solution
Answer to Problem 29WE
A right circular cone has many planes of symmetry containing the vertical axis AOand has only one axis of rotation that is the vertical axis AO .
Explanation of Solution
Given information:
The given figure is right circular cone.
The figure ofa right circular cone.
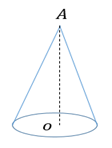
A right circular cone has many planes of symmetry containing the vertical axis AO as shown in figure because for each plane which contains AO the figure is symmetric. And the right circular cone has only one axis of rotation, the axis is AO because this is the only axis on which the rotation of the figure is symmetric.
b.
To determine
To write the number of planes of symmetry and the number of axes of the rotation the solid has.
b.
Expert Solution
Answer to Problem 29WE
A cube has nine planes of symmetry and seven axes of rotation.
Explanation of Solution
Given information:
The given figure is a cube.
The figure ofa cube.
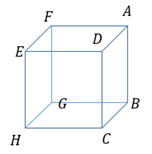
A cube has nine planes of symmetry. Assume the centroid of the cube is at the origin. All three principal planes are planes of symmetry.
Plane containing side BC and EF is a plane of symmetry.
Plane containing side AD and GH is a plane of symmetry.
Plane containing side AF and HC is a plane of symmetry.
Plane containing side ED and GB is a plane of symmetry.
Plane containing side AB and EH is a plane of symmetry.
Plane containing side FG and DC is a plane of symmetry.
A cube has seven axes of rotation.
Since it is assumed thatthe centroid of the cube is at the origin. Hence, all three principal axes are the axes of rotation because the figure is symmetric about all three principal axes.
Line passing through G and D is an axis of rotation.
Line passing through F and C is an axis of rotation.
Line passing through E and B is an axis of rotation.
Line passing through A and H is an axis of rotation.
c.
To determine
To draw the figure if there is one that meets the conditions.
c.
Expert Solution
Answer to Problem 29WE
A trapezoid has six planes of symmetry and four axe of rotation.
Explanation of Solution
Given information:
The given condition is that a parallelogram with just one symmetry line.
The figure of a trapezoid.
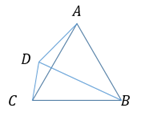
The above figure has six planes of symmetry. Each plane contains a side of any
The figure has four axes of rotationeach passes from a vertex of trapezoid and also passes from the centre of opposite triangle.
Chapter 14 Solutions
McDougal Littell Jurgensen Geometry: Student Edition Geometry
Ch. 14.1 - Prob. 1CECh. 14.1 - Prob. 2CECh. 14.1 - Prob. 3CECh. 14.1 - Prob. 4CECh. 14.1 - Prob. 5CECh. 14.1 - Prob. 6CECh. 14.1 - Prob. 7CECh. 14.1 - Prob. 8CECh. 14.1 - Prob. 9CECh. 14.1 - Prob. 10CE
Ch. 14.1 - Prob. 1WECh. 14.1 - Prob. 2WECh. 14.1 - Prob. 3WECh. 14.1 - Prob. 4WECh. 14.1 - Prob. 5WECh. 14.1 - Prob. 6WECh. 14.1 - Prob. 7WECh. 14.1 - Prob. 8WECh. 14.1 - Prob. 9WECh. 14.1 - Prob. 10WECh. 14.1 - Prob. 11WECh. 14.1 - Prob. 12WECh. 14.1 - Prob. 13WECh. 14.1 - Prob. 14WECh. 14.1 - Prob. 15WECh. 14.1 - Prob. 16WECh. 14.1 - Prob. 17WECh. 14.1 - Prob. 18WECh. 14.1 - Prob. 19WECh. 14.1 - Prob. 20WECh. 14.1 - Prob. 21WECh. 14.1 - Prob. 22WECh. 14.1 - Prob. 23WECh. 14.2 - Prob. 1CECh. 14.2 - Prob. 2CECh. 14.2 - Prob. 3CECh. 14.2 - Prob. 4CECh. 14.2 - Prob. 5CECh. 14.2 - Prob. 6CECh. 14.2 - Prob. 7CECh. 14.2 - Prob. 8CECh. 14.2 - Prob. 9CECh. 14.2 - Prob. 10CECh. 14.2 - Prob. 11CECh. 14.2 - Prob. 12CECh. 14.2 - Prob. 13CECh. 14.2 - Prob. 14CECh. 14.2 - Prob. 15CECh. 14.2 - Prob. 16CECh. 14.2 - Prob. 17CECh. 14.2 - Prob. 18CECh. 14.2 - Prob. 19CECh. 14.2 - Prob. 20CECh. 14.2 - Prob. 1WECh. 14.2 - Prob. 2WECh. 14.2 - Prob. 3WECh. 14.2 - Prob. 4WECh. 14.2 - Prob. 5WECh. 14.2 - Prob. 6WECh. 14.2 - Prob. 7WECh. 14.2 - Prob. 8WECh. 14.2 - Prob. 9WECh. 14.2 - Prob. 10WECh. 14.2 - Prob. 11WECh. 14.2 - Prob. 12WECh. 14.2 - Prob. 13WECh. 14.2 - Prob. 14WECh. 14.2 - Prob. 15WECh. 14.2 - Prob. 16WECh. 14.2 - Prob. 17WECh. 14.2 - Prob. 18WECh. 14.2 - Prob. 19WECh. 14.2 - Prob. 20WECh. 14.2 - Prob. 21WECh. 14.2 - Prob. 22WECh. 14.2 - Prob. 23WECh. 14.2 - Prob. 24WECh. 14.2 - Prob. 25WECh. 14.2 - Prob. 26WECh. 14.2 - Prob. 27WECh. 14.2 - Prob. 28WECh. 14.2 - Prob. 29WECh. 14.2 - Prob. 30WECh. 14.2 - Prob. 31WECh. 14.2 - Prob. 32WECh. 14.2 - Prob. 33WECh. 14.2 - Prob. 34WECh. 14.2 - Prob. 35WECh. 14.2 - Prob. 36WECh. 14.2 - Prob. 37WECh. 14.2 - Prob. 38WECh. 14.2 - Prob. 39WECh. 14.2 - Prob. 40WECh. 14.2 - Prob. 1ECh. 14.2 - Prob. 2ECh. 14.2 - Prob. 3ECh. 14.2 - Prob. 4ECh. 14.2 - Prob. 5ECh. 14.2 - Prob. 6ECh. 14.3 - Prob. 1CECh. 14.3 - Prob. 2CECh. 14.3 - Prob. 3CECh. 14.3 - Prob. 4CECh. 14.3 - Prob. 5CECh. 14.3 - Prob. 6CECh. 14.3 - Prob. 7CECh. 14.3 - Prob. 8CECh. 14.3 - Prob. 1WECh. 14.3 - Prob. 2WECh. 14.3 - Prob. 3WECh. 14.3 - Prob. 4WECh. 14.3 - Prob. 5WECh. 14.3 - Prob. 6WECh. 14.3 - Prob. 7WECh. 14.3 - Prob. 8WECh. 14.3 - Prob. 9WECh. 14.3 - Prob. 10WECh. 14.3 - Prob. 11WECh. 14.3 - Prob. 12WECh. 14.3 - Prob. 13WECh. 14.3 - Prob. 14WECh. 14.3 - Prob. 15WECh. 14.3 - Prob. 16WECh. 14.3 - Prob. 17WECh. 14.3 - Prob. 18WECh. 14.3 - Prob. 19WECh. 14.3 - Prob. 20WECh. 14.3 - Prob. 21WECh. 14.3 - Prob. 22WECh. 14.3 - Prob. 23WECh. 14.4 - Prob. 1CECh. 14.4 - Prob. 2CECh. 14.4 - Prob. 3CECh. 14.4 - Prob. 4CECh. 14.4 - Prob. 5CECh. 14.4 - Prob. 6CECh. 14.4 - Prob. 7CECh. 14.4 - Prob. 8CECh. 14.4 - Prob. 9CECh. 14.4 - Prob. 10CECh. 14.4 - Prob. 11CECh. 14.4 - Prob. 12CECh. 14.4 - Prob. 13CECh. 14.4 - Prob. 14CECh. 14.4 - Prob. 15CECh. 14.4 - Prob. 1WECh. 14.4 - Prob. 2WECh. 14.4 - Prob. 3WECh. 14.4 - Prob. 4WECh. 14.4 - Prob. 5WECh. 14.4 - Prob. 6WECh. 14.4 - Prob. 7WECh. 14.4 - Prob. 8WECh. 14.4 - Prob. 9WECh. 14.4 - Prob. 10WECh. 14.4 - Prob. 11WECh. 14.4 - Prob. 12WECh. 14.4 - Prob. 13WECh. 14.4 - Prob. 14WECh. 14.4 - Prob. 15WECh. 14.4 - Prob. 16WECh. 14.4 - Prob. 17WECh. 14.4 - Prob. 18WECh. 14.4 - Prob. 19WECh. 14.4 - Prob. 20WECh. 14.4 - Prob. 21WECh. 14.4 - Prob. 22WECh. 14.4 - Prob. 23WECh. 14.4 - Prob. 24WECh. 14.4 - Prob. 25WECh. 14.4 - Prob. 26WECh. 14.4 - Prob. 27WECh. 14.4 - Prob. 28WECh. 14.4 - Prob. 29WECh. 14.4 - Prob. 30WECh. 14.4 - Prob. 31WECh. 14.4 - Prob. 32WECh. 14.4 - Prob. 33WECh. 14.4 - Prob. 34WECh. 14.4 - Prob. 35WECh. 14.4 - Prob. 36WECh. 14.4 - Prob. 37WECh. 14.4 - Prob. 38WECh. 14.4 - Prob. 39WECh. 14.4 - Prob. 1MRECh. 14.4 - Prob. 2MRECh. 14.4 - Prob. 3MRECh. 14.4 - Prob. 4MRECh. 14.4 - Prob. 5MRECh. 14.4 - Prob. 6MRECh. 14.4 - Prob. 7MRECh. 14.5 - Prob. 1CECh. 14.5 - Prob. 2CECh. 14.5 - Prob. 3CECh. 14.5 - Prob. 4CECh. 14.5 - Prob. 5CECh. 14.5 - Prob. 6CECh. 14.5 - Prob. 7CECh. 14.5 - Prob. 8CECh. 14.5 - Prob. 9CECh. 14.5 - Prob. 10CECh. 14.5 - Prob. 11CECh. 14.5 - Prob. 12CECh. 14.5 - Prob. 13CECh. 14.5 - Prob. 14CECh. 14.5 - Prob. 15CECh. 14.5 - Prob. 16CECh. 14.5 - Prob. 17CECh. 14.5 - Prob. 1WECh. 14.5 - Prob. 2WECh. 14.5 - Prob. 3WECh. 14.5 - Prob. 4WECh. 14.5 - Prob. 5WECh. 14.5 - Prob. 6WECh. 14.5 - Prob. 7WECh. 14.5 - Prob. 8WECh. 14.5 - Prob. 9WECh. 14.5 - Prob. 10WECh. 14.5 - Prob. 11WECh. 14.5 - Prob. 12WECh. 14.5 - Prob. 13WECh. 14.5 - Prob. 14WECh. 14.5 - Prob. 15WECh. 14.5 - Prob. 16WECh. 14.5 - Prob. 17WECh. 14.5 - Prob. 18WECh. 14.5 - Prob. 19WECh. 14.5 - Prob. 20WECh. 14.5 - Prob. 21WECh. 14.5 - Prob. 22WECh. 14.5 - Prob. 23WECh. 14.5 - Prob. 24WECh. 14.5 - Prob. 25WECh. 14.5 - Prob. 26WECh. 14.5 - Prob. 27WECh. 14.5 - Prob. 28WECh. 14.5 - Prob. 1ST1Ch. 14.5 - Prob. 2ST1Ch. 14.5 - Prob. 3ST1Ch. 14.5 - Prob. 4ST1Ch. 14.5 - Prob. 5ST1Ch. 14.5 - Prob. 6ST1Ch. 14.5 - Prob. 7ST1Ch. 14.5 - Prob. 8ST1Ch. 14.5 - Prob. 9ST1Ch. 14.5 - Prob. 10ST1Ch. 14.5 - Prob. 11ST1Ch. 14.5 - Prob. 12ST1Ch. 14.5 - Prob. 13ST1Ch. 14.5 - Prob. 14ST1Ch. 14.5 - Prob. 15ST1Ch. 14.5 - Prob. 16ST1Ch. 14.5 - Prob. 17ST1Ch. 14.5 - Prob. 18ST1Ch. 14.6 - Prob. 1CECh. 14.6 - Prob. 2CECh. 14.6 - Prob. 3CECh. 14.6 - Prob. 4CECh. 14.6 - Prob. 5CECh. 14.6 - Prob. 6CECh. 14.6 - Prob. 7CECh. 14.6 - Prob. 8CECh. 14.6 - Prob. 9CECh. 14.6 - Prob. 10CECh. 14.6 - Prob. 11CECh. 14.6 - Prob. 12CECh. 14.6 - Prob. 1WECh. 14.6 - Prob. 2WECh. 14.6 - Prob. 3WECh. 14.6 - Prob. 4WECh. 14.6 - Prob. 5WECh. 14.6 - Prob. 6WECh. 14.6 - Prob. 7WECh. 14.6 - Prob. 8WECh. 14.6 - Prob. 9WECh. 14.6 - Prob. 10WECh. 14.6 - Prob. 11WECh. 14.6 - Prob. 12WECh. 14.6 - Prob. 13WECh. 14.6 - Prob. 14WECh. 14.6 - Prob. 15WECh. 14.6 - Prob. 16WECh. 14.6 - Prob. 17WECh. 14.6 - Prob. 18WECh. 14.6 - Prob. 19WECh. 14.6 - Prob. 20WECh. 14.6 - Prob. 21WECh. 14.6 - Prob. 22WECh. 14.6 - Prob. 23WECh. 14.6 - Prob. 24WECh. 14.6 - Prob. 25WECh. 14.6 - Prob. 26WECh. 14.6 - Prob. 27WECh. 14.6 - Prob. 28WECh. 14.6 - Prob. 29WECh. 14.6 - Prob. 30WECh. 14.7 - Prob. 1CECh. 14.7 - Prob. 2CECh. 14.7 - Prob. 3CECh. 14.7 - Prob. 4CECh. 14.7 - Prob. 5CECh. 14.7 - Prob. 6CECh. 14.7 - Prob. 7CECh. 14.7 - Prob. 8CECh. 14.7 - Prob. 9CECh. 14.7 - Prob. 10CECh. 14.7 - Prob. 11CECh. 14.7 - Prob. 12CECh. 14.7 - Prob. 13CECh. 14.7 - Prob. 14CECh. 14.7 - Prob. 15CECh. 14.7 - Prob. 16CECh. 14.7 - Prob. 17CECh. 14.7 - Prob. 18CECh. 14.7 - Prob. 19CECh. 14.7 - Prob. 20CECh. 14.7 - Prob. 21CECh. 14.7 - Prob. 22CECh. 14.7 - Prob. 23CECh. 14.7 - Prob. 24CECh. 14.7 - Prob. 1WECh. 14.7 - Prob. 2WECh. 14.7 - Prob. 3WECh. 14.7 - Prob. 4WECh. 14.7 - Prob. 5WECh. 14.7 - Prob. 6WECh. 14.7 - Prob. 7WECh. 14.7 - Prob. 8WECh. 14.7 - Prob. 9WECh. 14.7 - Prob. 10WECh. 14.7 - Prob. 11WECh. 14.7 - Prob. 12WECh. 14.7 - Prob. 13WECh. 14.7 - Prob. 14WECh. 14.7 - Prob. 15WECh. 14.7 - Prob. 16WECh. 14.7 - Prob. 17WECh. 14.7 - Prob. 18WECh. 14.7 - Prob. 19WECh. 14.7 - Prob. 20WECh. 14.7 - Prob. 21WECh. 14.7 - Prob. 22WECh. 14.7 - Prob. 23WECh. 14.7 - Prob. 24WECh. 14.7 - Prob. 25WECh. 14.7 - Prob. 26WECh. 14.7 - Prob. 27WECh. 14.7 - Prob. 28WECh. 14.7 - Prob. 29WECh. 14.7 - Prob. 30WECh. 14.7 - Prob. 31WECh. 14.8 - Prob. 1CECh. 14.8 - Prob. 2CECh. 14.8 - Prob. 3CECh. 14.8 - Prob. 4CECh. 14.8 - Prob. 5CECh. 14.8 - Prob. 6CECh. 14.8 - Prob. 7CECh. 14.8 - Prob. 8CECh. 14.8 - Prob. 9CECh. 14.8 - Prob. 10CECh. 14.8 - Prob. 11CECh. 14.8 - Prob. 12CECh. 14.8 - Prob. 13CECh. 14.8 - Prob. 14CECh. 14.8 - Prob. 15CECh. 14.8 - Prob. 1WECh. 14.8 - Prob. 2WECh. 14.8 - Prob. 3WECh. 14.8 - Prob. 4WECh. 14.8 - Prob. 5WECh. 14.8 - Prob. 6WECh. 14.8 - Prob. 7WECh. 14.8 - Prob. 8WECh. 14.8 - Prob. 9WECh. 14.8 - Prob. 10WECh. 14.8 - Prob. 11WECh. 14.8 - Prob. 12WECh. 14.8 - Prob. 13WECh. 14.8 - Prob. 14WECh. 14.8 - Prob. 15WECh. 14.8 - Prob. 16WECh. 14.8 - Prob. 17WECh. 14.8 - Prob. 18WECh. 14.8 - Prob. 19WECh. 14.8 - Prob. 20WECh. 14.8 - Prob. 21WECh. 14.8 - Prob. 22WECh. 14.8 - Prob. 23WECh. 14.8 - Prob. 25WECh. 14.8 - Prob. 26WECh. 14.8 - Prob. 27WECh. 14.8 - Prob. 28WECh. 14.8 - Prob. 29WECh. 14.8 - Prob. 1CCh. 14.8 - Prob. 2CCh. 14.8 - Prob. 1ST2Ch. 14.8 - Prob. 2ST2Ch. 14.8 - Prob. 3ST2Ch. 14.8 - Prob. 4ST2Ch. 14.8 - Prob. 5ST2Ch. 14.8 - Prob. 6ST2Ch. 14.8 - Prob. 7ST2Ch. 14.8 - Prob. 8ST2Ch. 14.8 - Prob. 9ST2Ch. 14.8 - Prob. 10ST2Ch. 14.8 - Prob. 11ST2Ch. 14.8 - Prob. 1ECh. 14.8 - Prob. 2ECh. 14.8 - Prob. 3ECh. 14.8 - Prob. 4ECh. 14.8 - Prob. 5ECh. 14.8 - Prob. 6ECh. 14.8 - Prob. 7ECh. 14.8 - Prob. 8ECh. 14.8 - Prob. 9ECh. 14.8 - Prob. 10ECh. 14 - Prob. 1CRCh. 14 - Prob. 2CRCh. 14 - Prob. 3CRCh. 14 - Prob. 4CRCh. 14 - Prob. 5CRCh. 14 - Prob. 6CRCh. 14 - Prob. 7CRCh. 14 - Prob. 8CRCh. 14 - Prob. 9CRCh. 14 - Prob. 10CRCh. 14 - Prob. 11CRCh. 14 - Prob. 12CRCh. 14 - Prob. 13CRCh. 14 - Prob. 14CRCh. 14 - Prob. 15CRCh. 14 - Prob. 16CRCh. 14 - Prob. 17CRCh. 14 - Prob. 18CRCh. 14 - Prob. 19CRCh. 14 - Prob. 20CRCh. 14 - Prob. 1CTCh. 14 - Prob. 2CTCh. 14 - Prob. 3CTCh. 14 - Prob. 4CTCh. 14 - Prob. 5CTCh. 14 - Prob. 6CTCh. 14 - Prob. 7CTCh. 14 - Prob. 8CTCh. 14 - Prob. 9CTCh. 14 - Prob. 10CTCh. 14 - Prob. 11CTCh. 14 - Prob. 12CTCh. 14 - Prob. 13CTCh. 14 - Prob. 14CTCh. 14 - Prob. 15CTCh. 14 - Prob. 16CTCh. 14 - Prob. 17CTCh. 14 - Prob. 18CTCh. 14 - Prob. 19CTCh. 14 - Prob. 20CTCh. 14 - Prob. 21CTCh. 14 - Prob. 22CTCh. 14 - Prob. 23CTCh. 14 - Prob. 24CTCh. 14 - Prob. 25CTCh. 14 - Prob. 1CURCh. 14 - Prob. 2CURCh. 14 - Prob. 3CURCh. 14 - Prob. 4CURCh. 14 - Prob. 5CURCh. 14 - Prob. 6CURCh. 14 - Prob. 7CURCh. 14 - Prob. 8CURCh. 14 - Prob. 9CURCh. 14 - Prob. 10CURCh. 14 - Prob. 11CURCh. 14 - Prob. 12CURCh. 14 - Prob. 13CURCh. 14 - Prob. 14CURCh. 14 - Prob. 15CURCh. 14 - Prob. 16CURCh. 14 - Prob. 17CURCh. 14 - Prob. 18CURCh. 14 - Prob. 19CURCh. 14 - Prob. 20CURCh. 14 - Prob. 1MCECh. 14 - Prob. 2MCECh. 14 - Prob. 3MCECh. 14 - Prob. 4MCECh. 14 - Prob. 5MCECh. 14 - Prob. 6MCECh. 14 - Prob. 7MCECh. 14 - Prob. 8MCECh. 14 - Prob. 9MCECh. 14 - Prob. 10MCECh. 14 - Prob. 11MCECh. 14 - Prob. 1CPECh. 14 - Prob. 2CPECh. 14 - Prob. 3CPECh. 14 - Prob. 4CPECh. 14 - Prob. 5CPECh. 14 - Prob. 6CPECh. 14 - Prob. 7CPECh. 14 - Prob. 8CPECh. 14 - Prob. 9CPECh. 14 - Prob. 10CPECh. 14 - Prob. 11CPECh. 14 - Prob. 12CPECh. 14 - Prob. 13CPECh. 14 - Prob. 14CPECh. 14 - Prob. 15CPECh. 14 - Prob. 16CPECh. 14 - Prob. 17CPECh. 14 - Prob. 18CPECh. 14 - Prob. 19CPECh. 14 - Prob. 20CPECh. 14 - Prob. 21CPECh. 14 - Prob. 1ASNECh. 14 - Prob. 2ASNECh. 14 - Prob. 3ASNECh. 14 - Prob. 4ASNECh. 14 - Prob. 5ASNECh. 14 - Prob. 6ASNECh. 14 - Prob. 7ASNECh. 14 - Prob. 8ASNECh. 14 - Prob. 9ASNECh. 14 - Prob. 10ASNECh. 14 - Prob. 11ASNECh. 14 - Prob. 12ASNECh. 14 - Prob. 13ASNECh. 14 - Prob. 14ASNECh. 14 - Prob. 15ASNECh. 14 - Prob. 16ASNECh. 14 - Prob. 17ASNECh. 14 - Prob. 1CTECh. 14 - Prob. 2CTECh. 14 - Prob. 3CTECh. 14 - Prob. 4CTECh. 14 - Prob. 5CTECh. 14 - Prob. 6CTECh. 14 - Prob. 7CTECh. 14 - Prob. 8CTECh. 14 - Prob. 1PECh. 14 - Prob. 2PECh. 14 - Prob. 3PECh. 14 - Prob. 4PECh. 14 - Prob. 5PECh. 14 - Prob. 6PECh. 14 - Prob. 7PE
Additional Math Textbook Solutions
Find more solutions based on key concepts
Assessment 1-1A Cookies are sold singly or in packages of 2 or 6. With this packaging, how many ways can you bu...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Sum of the given expression
Pre-Algebra Student Edition
CHECK POINT I Express as a percent.
Thinking Mathematically (6th Edition)
The table by using the given graph of h.
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
IQ Scores. In Exercises 9–12, find the indicated IQ score and round to the nearest whole number. The graphs dep...
Elementary Statistics (13th Edition)
Fill in each blank so that the resulting statement is true. If n is a counting number, bn, read ______, indicat...
College Algebra (7th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- ◆ Switch To Light Mode HOMEWORK: 18, 19, 24, 27, 29 ***Please refer to the HOMEWORK sheet from Thursday, 9/14, for the problems ****Please text or email me if you have any questions 18. Figure 5-35 is a map of downtown Royalton, showing the Royalton River running through the downtown area and the three islands (A, B, and C) connected to each other and both banks by eight bridges. The Down- town Athletic Club wants to design the route for a marathon through the downtown area. Draw a graph that models the layout of Royalton. FIGURE 5-35 North Royalton Royalton River South Royption 19. A night watchman must walk the streets of the Green Hills subdivision shown in Fig. 5-36. The night watch- man needs to walk only once along each block. Draw a graph that models this situation.arrow_forwardSolve this question and check if my answer provided is correctarrow_forwardProof: LN⎯⎯⎯⎯⎯LN¯ divides quadrilateral KLMN into two triangles. The sum of the angle measures in each triangle is ˚, so the sum of the angle measures for both triangles is ˚. So, m∠K+m∠L+m∠M+m∠N=m∠K+m∠L+m∠M+m∠N=˚. Because ∠K≅∠M∠K≅∠M and ∠N≅∠L, m∠K=m∠M∠N≅∠L, m∠K=m∠M and m∠N=m∠Lm∠N=m∠L by the definition of congruence. By the Substitution Property of Equality, m∠K+m∠L+m∠K+m∠L=m∠K+m∠L+m∠K+m∠L=°,°, so (m∠K)+ m∠K+ (m∠L)= m∠L= ˚. Dividing each side by gives m∠K+m∠L=m∠K+m∠L= °.°. The consecutive angles are supplementary, so KN⎯⎯⎯⎯⎯⎯∥LM⎯⎯⎯⎯⎯⎯KN¯∥LM¯ by the Converse of the Consecutive Interior Angles Theorem. Likewise, (m∠K)+m∠K+ (m∠N)=m∠N= ˚, or m∠K+m∠N=m∠K+m∠N= ˚. So these consecutive angles are supplementary and KL⎯⎯⎯⎯⎯∥NM⎯⎯⎯⎯⎯⎯KL¯∥NM¯ by the Converse of the Consecutive Interior Angles Theorem. Opposite sides are parallel, so quadrilateral KLMN is a parallelogram.arrow_forward
- Quadrilateral BCDE is similar to quadrilateral FGHI. Find the measure of side FG. Round your answer to the nearest tenth if necessary. BCDEFGHI2737.55arrow_forwardAn angle measures 70.6° more than the measure of its supplementary angle. What is the measure of each angle?arrow_forwardName: Date: Per: Unit 7: Geometry Homework 4: Parallel Lines & Transversals **This is a 2-page document! ** Directions: Classify each angle pair and indicate whether they are congruent or supplementary. 1 1.23 and 25 2. 24 and 28 3. 22 and 25 4. 22 and 28 5. 21 and 27 6. 22 and 26 Directions: Find each angle measure. 7. Given: wvm25-149 m21- 8. Given: mn: m1=74 mz2- m22- m.23- m23- mz4= V mz4= m25= m26- m26= m27- m27 m28- m48= 9. Given: a || b: m28 125 m2- 10. Given: xy: m22-22 m21- = mz2- m43- m3- mZA m24-> m. 5- m25- m26- m.26=> m2]=> m27= m28- 11. Given: rm2-29: m15-65 m2=> m29-> m3- m. 10- mc4= m25= m212- m.46- m213- mat- m214- m28- & Gina when (N) Things ALICE 2017arrow_forward
- Match each statement to the set of shapes that best describes them. 1. Similar triangles by SSS 2. Similar triangles by SAS 3. Similar triangles by AA 4. The triangles are not similar > U E 35° 89° S F 89° J 35° 94° G 52° 90° E K 52° Iarrow_forwardMatch each transformation series with the diagram that applies to it. 1. (x, y) (x-10, y + 7) scale factor: 2 2. (x, y)(x-8, y+6) scale factor: 4 3. (x, y)(x+1, y - 5) scale factor: 5 D' 104º 6 2 -10 8 -6 F2 4 5 D 2 E -4 -6 100 E 8 10 Farrow_forwardWhich sets of figures below are similar? Select all that apply. 48 yd 48 yd G 48 yd 26 mm 40 m 23 km 25 m 22 mm 37 mm 25 mi 42 yd 48 yd 48 yd 48 yd U 42 yd 25 mm M T 40 mi 20 mm 25 mm 30 mi 48 m K 37 mm 20 mm 48 m S 30 mi 73 km 29 km 29 kmarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Orthogonality in Inner Product Spaces; Author: Study Force;https://www.youtube.com/watch?v=RzIx_rRo9m0;License: Standard YouTube License, CC-BY
Abstract Algebra: The definition of a Group; Author: Socratica;https://www.youtube.com/watch?v=QudbrUcVPxk;License: Standard Youtube License