McDougal Littell Jurgensen Geometry: Student Edition Geometry
5th Edition
ISBN: 9780395977279
Author: Ray C. Jurgensen, Richard G. Brown, John W. Jurgensen
Publisher: Houghton Mifflin Company College Division
expand_more
expand_more
format_list_bulleted
Question
Chapter 14.8, Problem 12CE
(a)
To determine
To find: The translational symmetry of the pattern.
(a)
Expert Solution
Answer to Problem 12CE
The pattern is not a translational symmetry.
Explanation of Solution
Given information:
The given pattern design is shown below.
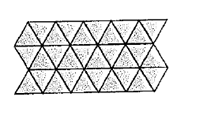
Calculation:
A design can also have translation symmetry if there is a translation that maps the figure onto itself.
Translational symmetry occurs only in pattern that cover a plane. But the given pattern is asymmetrical in nature so it is not a translational symmetry.
Therefore, the pattern is not a translational symmetry.
(b)
To determine
To find: Line symmetry of the pattern.
(b)
Expert Solution
Answer to Problem 12CE
The given pattern is not a line symmetry.
Explanation of Solution
Given information:
The given pattern design shown below.
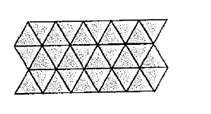
Calculation:
The line of symmetry is the imaginary line where fold the image and have both halves match exactly.
In the above pattern draw a line of axis then fold along that line the parts of object sides of the line not exactly coincide.
Hence the given pattern is not a line symmetry.
Therefore, the given pattern is not a line symmetry.
(c)
To determine
To find: Point symmetry of the pattern.
(c)
Expert Solution
Answer to Problem 12CE
The pattern is not a point symmetry.
Explanation of Solution
Given information:
The given pattern design shown below.
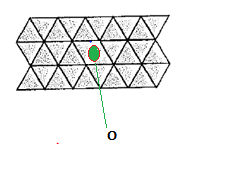
Calculation:
Point symmetry occurs when there exists a point on an object that splits the object into two parts in which each part has a matching part the same distance from the central point, and face different directions.
The given pattern is asymmetrical in nature , therefore the pattern is not a point symmetry.
Therefore, the pattern is not a point symmetry.
(d)
To determine
To find: The rotational symmetry of the pattern.
(d)
Expert Solution
Answer to Problem 12CE
The pattern is not a rotational symmetry.
Explanation of Solution
Given information:
The given pattern design is shown below.
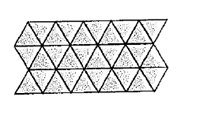
Calculation:
A shape has a rotational symmetry when it still looks the same after some rotation.
The given pattern is not symmetry if rotated because the shape is asymmetrical.
Therefore, the pattern is not a rotational symmetry.
Chapter 14 Solutions
McDougal Littell Jurgensen Geometry: Student Edition Geometry
Ch. 14.1 - Prob. 1CECh. 14.1 - Prob. 2CECh. 14.1 - Prob. 3CECh. 14.1 - Prob. 4CECh. 14.1 - Prob. 5CECh. 14.1 - Prob. 6CECh. 14.1 - Prob. 7CECh. 14.1 - Prob. 8CECh. 14.1 - Prob. 9CECh. 14.1 - Prob. 10CE
Ch. 14.1 - Prob. 1WECh. 14.1 - Prob. 2WECh. 14.1 - Prob. 3WECh. 14.1 - Prob. 4WECh. 14.1 - Prob. 5WECh. 14.1 - Prob. 6WECh. 14.1 - Prob. 7WECh. 14.1 - Prob. 8WECh. 14.1 - Prob. 9WECh. 14.1 - Prob. 10WECh. 14.1 - Prob. 11WECh. 14.1 - Prob. 12WECh. 14.1 - Prob. 13WECh. 14.1 - Prob. 14WECh. 14.1 - Prob. 15WECh. 14.1 - Prob. 16WECh. 14.1 - Prob. 17WECh. 14.1 - Prob. 18WECh. 14.1 - Prob. 19WECh. 14.1 - Prob. 20WECh. 14.1 - Prob. 21WECh. 14.1 - Prob. 22WECh. 14.1 - Prob. 23WECh. 14.2 - Prob. 1CECh. 14.2 - Prob. 2CECh. 14.2 - Prob. 3CECh. 14.2 - Prob. 4CECh. 14.2 - Prob. 5CECh. 14.2 - Prob. 6CECh. 14.2 - Prob. 7CECh. 14.2 - Prob. 8CECh. 14.2 - Prob. 9CECh. 14.2 - Prob. 10CECh. 14.2 - Prob. 11CECh. 14.2 - Prob. 12CECh. 14.2 - Prob. 13CECh. 14.2 - Prob. 14CECh. 14.2 - Prob. 15CECh. 14.2 - Prob. 16CECh. 14.2 - Prob. 17CECh. 14.2 - Prob. 18CECh. 14.2 - Prob. 19CECh. 14.2 - Prob. 20CECh. 14.2 - Prob. 1WECh. 14.2 - Prob. 2WECh. 14.2 - Prob. 3WECh. 14.2 - Prob. 4WECh. 14.2 - Prob. 5WECh. 14.2 - Prob. 6WECh. 14.2 - Prob. 7WECh. 14.2 - Prob. 8WECh. 14.2 - Prob. 9WECh. 14.2 - Prob. 10WECh. 14.2 - Prob. 11WECh. 14.2 - Prob. 12WECh. 14.2 - Prob. 13WECh. 14.2 - Prob. 14WECh. 14.2 - Prob. 15WECh. 14.2 - Prob. 16WECh. 14.2 - Prob. 17WECh. 14.2 - Prob. 18WECh. 14.2 - Prob. 19WECh. 14.2 - Prob. 20WECh. 14.2 - Prob. 21WECh. 14.2 - Prob. 22WECh. 14.2 - Prob. 23WECh. 14.2 - Prob. 24WECh. 14.2 - Prob. 25WECh. 14.2 - Prob. 26WECh. 14.2 - Prob. 27WECh. 14.2 - Prob. 28WECh. 14.2 - Prob. 29WECh. 14.2 - Prob. 30WECh. 14.2 - Prob. 31WECh. 14.2 - Prob. 32WECh. 14.2 - Prob. 33WECh. 14.2 - Prob. 34WECh. 14.2 - Prob. 35WECh. 14.2 - Prob. 36WECh. 14.2 - Prob. 37WECh. 14.2 - Prob. 38WECh. 14.2 - Prob. 39WECh. 14.2 - Prob. 40WECh. 14.2 - Prob. 1ECh. 14.2 - Prob. 2ECh. 14.2 - Prob. 3ECh. 14.2 - Prob. 4ECh. 14.2 - Prob. 5ECh. 14.2 - Prob. 6ECh. 14.3 - Prob. 1CECh. 14.3 - Prob. 2CECh. 14.3 - Prob. 3CECh. 14.3 - Prob. 4CECh. 14.3 - Prob. 5CECh. 14.3 - Prob. 6CECh. 14.3 - Prob. 7CECh. 14.3 - Prob. 8CECh. 14.3 - Prob. 1WECh. 14.3 - Prob. 2WECh. 14.3 - Prob. 3WECh. 14.3 - Prob. 4WECh. 14.3 - Prob. 5WECh. 14.3 - Prob. 6WECh. 14.3 - Prob. 7WECh. 14.3 - Prob. 8WECh. 14.3 - Prob. 9WECh. 14.3 - Prob. 10WECh. 14.3 - Prob. 11WECh. 14.3 - Prob. 12WECh. 14.3 - Prob. 13WECh. 14.3 - Prob. 14WECh. 14.3 - Prob. 15WECh. 14.3 - Prob. 16WECh. 14.3 - Prob. 17WECh. 14.3 - Prob. 18WECh. 14.3 - Prob. 19WECh. 14.3 - Prob. 20WECh. 14.3 - Prob. 21WECh. 14.3 - Prob. 22WECh. 14.3 - Prob. 23WECh. 14.4 - Prob. 1CECh. 14.4 - Prob. 2CECh. 14.4 - Prob. 3CECh. 14.4 - Prob. 4CECh. 14.4 - Prob. 5CECh. 14.4 - Prob. 6CECh. 14.4 - Prob. 7CECh. 14.4 - Prob. 8CECh. 14.4 - Prob. 9CECh. 14.4 - Prob. 10CECh. 14.4 - Prob. 11CECh. 14.4 - Prob. 12CECh. 14.4 - Prob. 13CECh. 14.4 - Prob. 14CECh. 14.4 - Prob. 15CECh. 14.4 - Prob. 1WECh. 14.4 - Prob. 2WECh. 14.4 - Prob. 3WECh. 14.4 - Prob. 4WECh. 14.4 - Prob. 5WECh. 14.4 - Prob. 6WECh. 14.4 - Prob. 7WECh. 14.4 - Prob. 8WECh. 14.4 - Prob. 9WECh. 14.4 - Prob. 10WECh. 14.4 - Prob. 11WECh. 14.4 - Prob. 12WECh. 14.4 - Prob. 13WECh. 14.4 - Prob. 14WECh. 14.4 - Prob. 15WECh. 14.4 - Prob. 16WECh. 14.4 - Prob. 17WECh. 14.4 - Prob. 18WECh. 14.4 - Prob. 19WECh. 14.4 - Prob. 20WECh. 14.4 - Prob. 21WECh. 14.4 - Prob. 22WECh. 14.4 - Prob. 23WECh. 14.4 - Prob. 24WECh. 14.4 - Prob. 25WECh. 14.4 - Prob. 26WECh. 14.4 - Prob. 27WECh. 14.4 - Prob. 28WECh. 14.4 - Prob. 29WECh. 14.4 - Prob. 30WECh. 14.4 - Prob. 31WECh. 14.4 - Prob. 32WECh. 14.4 - Prob. 33WECh. 14.4 - Prob. 34WECh. 14.4 - Prob. 35WECh. 14.4 - Prob. 36WECh. 14.4 - Prob. 37WECh. 14.4 - Prob. 38WECh. 14.4 - Prob. 39WECh. 14.4 - Prob. 1MRECh. 14.4 - Prob. 2MRECh. 14.4 - Prob. 3MRECh. 14.4 - Prob. 4MRECh. 14.4 - Prob. 5MRECh. 14.4 - Prob. 6MRECh. 14.4 - Prob. 7MRECh. 14.5 - Prob. 1CECh. 14.5 - Prob. 2CECh. 14.5 - Prob. 3CECh. 14.5 - Prob. 4CECh. 14.5 - Prob. 5CECh. 14.5 - Prob. 6CECh. 14.5 - Prob. 7CECh. 14.5 - Prob. 8CECh. 14.5 - Prob. 9CECh. 14.5 - Prob. 10CECh. 14.5 - Prob. 11CECh. 14.5 - Prob. 12CECh. 14.5 - Prob. 13CECh. 14.5 - Prob. 14CECh. 14.5 - Prob. 15CECh. 14.5 - Prob. 16CECh. 14.5 - Prob. 17CECh. 14.5 - Prob. 1WECh. 14.5 - Prob. 2WECh. 14.5 - Prob. 3WECh. 14.5 - Prob. 4WECh. 14.5 - Prob. 5WECh. 14.5 - Prob. 6WECh. 14.5 - Prob. 7WECh. 14.5 - Prob. 8WECh. 14.5 - Prob. 9WECh. 14.5 - Prob. 10WECh. 14.5 - Prob. 11WECh. 14.5 - Prob. 12WECh. 14.5 - Prob. 13WECh. 14.5 - Prob. 14WECh. 14.5 - Prob. 15WECh. 14.5 - Prob. 16WECh. 14.5 - Prob. 17WECh. 14.5 - Prob. 18WECh. 14.5 - Prob. 19WECh. 14.5 - Prob. 20WECh. 14.5 - Prob. 21WECh. 14.5 - Prob. 22WECh. 14.5 - Prob. 23WECh. 14.5 - Prob. 24WECh. 14.5 - Prob. 25WECh. 14.5 - Prob. 26WECh. 14.5 - Prob. 27WECh. 14.5 - Prob. 28WECh. 14.5 - Prob. 1ST1Ch. 14.5 - Prob. 2ST1Ch. 14.5 - Prob. 3ST1Ch. 14.5 - Prob. 4ST1Ch. 14.5 - Prob. 5ST1Ch. 14.5 - Prob. 6ST1Ch. 14.5 - Prob. 7ST1Ch. 14.5 - Prob. 8ST1Ch. 14.5 - Prob. 9ST1Ch. 14.5 - Prob. 10ST1Ch. 14.5 - Prob. 11ST1Ch. 14.5 - Prob. 12ST1Ch. 14.5 - Prob. 13ST1Ch. 14.5 - Prob. 14ST1Ch. 14.5 - Prob. 15ST1Ch. 14.5 - Prob. 16ST1Ch. 14.5 - Prob. 17ST1Ch. 14.5 - Prob. 18ST1Ch. 14.6 - Prob. 1CECh. 14.6 - Prob. 2CECh. 14.6 - Prob. 3CECh. 14.6 - Prob. 4CECh. 14.6 - Prob. 5CECh. 14.6 - Prob. 6CECh. 14.6 - Prob. 7CECh. 14.6 - Prob. 8CECh. 14.6 - Prob. 9CECh. 14.6 - Prob. 10CECh. 14.6 - Prob. 11CECh. 14.6 - Prob. 12CECh. 14.6 - Prob. 1WECh. 14.6 - Prob. 2WECh. 14.6 - Prob. 3WECh. 14.6 - Prob. 4WECh. 14.6 - Prob. 5WECh. 14.6 - Prob. 6WECh. 14.6 - Prob. 7WECh. 14.6 - Prob. 8WECh. 14.6 - Prob. 9WECh. 14.6 - Prob. 10WECh. 14.6 - Prob. 11WECh. 14.6 - Prob. 12WECh. 14.6 - Prob. 13WECh. 14.6 - Prob. 14WECh. 14.6 - Prob. 15WECh. 14.6 - Prob. 16WECh. 14.6 - Prob. 17WECh. 14.6 - Prob. 18WECh. 14.6 - Prob. 19WECh. 14.6 - Prob. 20WECh. 14.6 - Prob. 21WECh. 14.6 - Prob. 22WECh. 14.6 - Prob. 23WECh. 14.6 - Prob. 24WECh. 14.6 - Prob. 25WECh. 14.6 - Prob. 26WECh. 14.6 - Prob. 27WECh. 14.6 - Prob. 28WECh. 14.6 - Prob. 29WECh. 14.6 - Prob. 30WECh. 14.7 - Prob. 1CECh. 14.7 - Prob. 2CECh. 14.7 - Prob. 3CECh. 14.7 - Prob. 4CECh. 14.7 - Prob. 5CECh. 14.7 - Prob. 6CECh. 14.7 - Prob. 7CECh. 14.7 - Prob. 8CECh. 14.7 - Prob. 9CECh. 14.7 - Prob. 10CECh. 14.7 - Prob. 11CECh. 14.7 - Prob. 12CECh. 14.7 - Prob. 13CECh. 14.7 - Prob. 14CECh. 14.7 - Prob. 15CECh. 14.7 - Prob. 16CECh. 14.7 - Prob. 17CECh. 14.7 - Prob. 18CECh. 14.7 - Prob. 19CECh. 14.7 - Prob. 20CECh. 14.7 - Prob. 21CECh. 14.7 - Prob. 22CECh. 14.7 - Prob. 23CECh. 14.7 - Prob. 24CECh. 14.7 - Prob. 1WECh. 14.7 - Prob. 2WECh. 14.7 - Prob. 3WECh. 14.7 - Prob. 4WECh. 14.7 - Prob. 5WECh. 14.7 - Prob. 6WECh. 14.7 - Prob. 7WECh. 14.7 - Prob. 8WECh. 14.7 - Prob. 9WECh. 14.7 - Prob. 10WECh. 14.7 - Prob. 11WECh. 14.7 - Prob. 12WECh. 14.7 - Prob. 13WECh. 14.7 - Prob. 14WECh. 14.7 - Prob. 15WECh. 14.7 - Prob. 16WECh. 14.7 - Prob. 17WECh. 14.7 - Prob. 18WECh. 14.7 - Prob. 19WECh. 14.7 - Prob. 20WECh. 14.7 - Prob. 21WECh. 14.7 - Prob. 22WECh. 14.7 - Prob. 23WECh. 14.7 - Prob. 24WECh. 14.7 - Prob. 25WECh. 14.7 - Prob. 26WECh. 14.7 - Prob. 27WECh. 14.7 - Prob. 28WECh. 14.7 - Prob. 29WECh. 14.7 - Prob. 30WECh. 14.7 - Prob. 31WECh. 14.8 - Prob. 1CECh. 14.8 - Prob. 2CECh. 14.8 - Prob. 3CECh. 14.8 - Prob. 4CECh. 14.8 - Prob. 5CECh. 14.8 - Prob. 6CECh. 14.8 - Prob. 7CECh. 14.8 - Prob. 8CECh. 14.8 - Prob. 9CECh. 14.8 - Prob. 10CECh. 14.8 - Prob. 11CECh. 14.8 - Prob. 12CECh. 14.8 - Prob. 13CECh. 14.8 - Prob. 14CECh. 14.8 - Prob. 15CECh. 14.8 - Prob. 1WECh. 14.8 - Prob. 2WECh. 14.8 - Prob. 3WECh. 14.8 - Prob. 4WECh. 14.8 - Prob. 5WECh. 14.8 - Prob. 6WECh. 14.8 - Prob. 7WECh. 14.8 - Prob. 8WECh. 14.8 - Prob. 9WECh. 14.8 - Prob. 10WECh. 14.8 - Prob. 11WECh. 14.8 - Prob. 12WECh. 14.8 - Prob. 13WECh. 14.8 - Prob. 14WECh. 14.8 - Prob. 15WECh. 14.8 - Prob. 16WECh. 14.8 - Prob. 17WECh. 14.8 - Prob. 18WECh. 14.8 - Prob. 19WECh. 14.8 - Prob. 20WECh. 14.8 - Prob. 21WECh. 14.8 - Prob. 22WECh. 14.8 - Prob. 23WECh. 14.8 - Prob. 25WECh. 14.8 - Prob. 26WECh. 14.8 - Prob. 27WECh. 14.8 - Prob. 28WECh. 14.8 - Prob. 29WECh. 14.8 - Prob. 1CCh. 14.8 - Prob. 2CCh. 14.8 - Prob. 1ST2Ch. 14.8 - Prob. 2ST2Ch. 14.8 - Prob. 3ST2Ch. 14.8 - Prob. 4ST2Ch. 14.8 - Prob. 5ST2Ch. 14.8 - Prob. 6ST2Ch. 14.8 - Prob. 7ST2Ch. 14.8 - Prob. 8ST2Ch. 14.8 - Prob. 9ST2Ch. 14.8 - Prob. 10ST2Ch. 14.8 - Prob. 11ST2Ch. 14.8 - Prob. 1ECh. 14.8 - Prob. 2ECh. 14.8 - Prob. 3ECh. 14.8 - Prob. 4ECh. 14.8 - Prob. 5ECh. 14.8 - Prob. 6ECh. 14.8 - Prob. 7ECh. 14.8 - Prob. 8ECh. 14.8 - Prob. 9ECh. 14.8 - Prob. 10ECh. 14 - Prob. 1CRCh. 14 - Prob. 2CRCh. 14 - Prob. 3CRCh. 14 - Prob. 4CRCh. 14 - Prob. 5CRCh. 14 - Prob. 6CRCh. 14 - Prob. 7CRCh. 14 - Prob. 8CRCh. 14 - Prob. 9CRCh. 14 - Prob. 10CRCh. 14 - Prob. 11CRCh. 14 - Prob. 12CRCh. 14 - Prob. 13CRCh. 14 - Prob. 14CRCh. 14 - Prob. 15CRCh. 14 - Prob. 16CRCh. 14 - Prob. 17CRCh. 14 - Prob. 18CRCh. 14 - Prob. 19CRCh. 14 - Prob. 20CRCh. 14 - Prob. 1CTCh. 14 - Prob. 2CTCh. 14 - Prob. 3CTCh. 14 - Prob. 4CTCh. 14 - Prob. 5CTCh. 14 - Prob. 6CTCh. 14 - Prob. 7CTCh. 14 - Prob. 8CTCh. 14 - Prob. 9CTCh. 14 - Prob. 10CTCh. 14 - Prob. 11CTCh. 14 - Prob. 12CTCh. 14 - Prob. 13CTCh. 14 - Prob. 14CTCh. 14 - Prob. 15CTCh. 14 - Prob. 16CTCh. 14 - Prob. 17CTCh. 14 - Prob. 18CTCh. 14 - Prob. 19CTCh. 14 - Prob. 20CTCh. 14 - Prob. 21CTCh. 14 - Prob. 22CTCh. 14 - Prob. 23CTCh. 14 - Prob. 24CTCh. 14 - Prob. 25CTCh. 14 - Prob. 1CURCh. 14 - Prob. 2CURCh. 14 - Prob. 3CURCh. 14 - Prob. 4CURCh. 14 - Prob. 5CURCh. 14 - Prob. 6CURCh. 14 - Prob. 7CURCh. 14 - Prob. 8CURCh. 14 - Prob. 9CURCh. 14 - Prob. 10CURCh. 14 - Prob. 11CURCh. 14 - Prob. 12CURCh. 14 - Prob. 13CURCh. 14 - Prob. 14CURCh. 14 - Prob. 15CURCh. 14 - Prob. 16CURCh. 14 - Prob. 17CURCh. 14 - Prob. 18CURCh. 14 - Prob. 19CURCh. 14 - Prob. 20CURCh. 14 - Prob. 1MCECh. 14 - Prob. 2MCECh. 14 - Prob. 3MCECh. 14 - Prob. 4MCECh. 14 - Prob. 5MCECh. 14 - Prob. 6MCECh. 14 - Prob. 7MCECh. 14 - Prob. 8MCECh. 14 - Prob. 9MCECh. 14 - Prob. 10MCECh. 14 - Prob. 11MCECh. 14 - Prob. 1CPECh. 14 - Prob. 2CPECh. 14 - Prob. 3CPECh. 14 - Prob. 4CPECh. 14 - Prob. 5CPECh. 14 - Prob. 6CPECh. 14 - Prob. 7CPECh. 14 - Prob. 8CPECh. 14 - Prob. 9CPECh. 14 - Prob. 10CPECh. 14 - Prob. 11CPECh. 14 - Prob. 12CPECh. 14 - Prob. 13CPECh. 14 - Prob. 14CPECh. 14 - Prob. 15CPECh. 14 - Prob. 16CPECh. 14 - Prob. 17CPECh. 14 - Prob. 18CPECh. 14 - Prob. 19CPECh. 14 - Prob. 20CPECh. 14 - Prob. 21CPECh. 14 - Prob. 1ASNECh. 14 - Prob. 2ASNECh. 14 - Prob. 3ASNECh. 14 - Prob. 4ASNECh. 14 - Prob. 5ASNECh. 14 - Prob. 6ASNECh. 14 - Prob. 7ASNECh. 14 - Prob. 8ASNECh. 14 - Prob. 9ASNECh. 14 - Prob. 10ASNECh. 14 - Prob. 11ASNECh. 14 - Prob. 12ASNECh. 14 - Prob. 13ASNECh. 14 - Prob. 14ASNECh. 14 - Prob. 15ASNECh. 14 - Prob. 16ASNECh. 14 - Prob. 17ASNECh. 14 - Prob. 1CTECh. 14 - Prob. 2CTECh. 14 - Prob. 3CTECh. 14 - Prob. 4CTECh. 14 - Prob. 5CTECh. 14 - Prob. 6CTECh. 14 - Prob. 7CTECh. 14 - Prob. 8CTECh. 14 - Prob. 1PECh. 14 - Prob. 2PECh. 14 - Prob. 3PECh. 14 - Prob. 4PECh. 14 - Prob. 5PECh. 14 - Prob. 6PECh. 14 - Prob. 7PE
Additional Math Textbook Solutions
Find more solutions based on key concepts
TRY IT YOURSELF 1
Find the mean of the points scored by the 51 winning teams listed on page 39.
Elementary Statistics: Picturing the World (7th Edition)
Derivative Calculations
In Exercises 112, find the first and second derivatives.
3. s = 5t3 – 3t5
University Calculus: Early Transcendentals (4th Edition)
Limits of sequences Find the limit of the following sequences or determine that the limit does not exist. 23. {...
Calculus: Early Transcendentals (2nd Edition)
Whether the requirements for a hypothesis test are satisfied or not.
Elementary Statistics
Siblings The histogram shows the distribution of the numbers of siblings (brothers and sisters) for 2000 adults...
Introductory Statistics
Continuous Uniform Distribution. In Exercises 5–8, refer to the continuous uniform distribution depicted in Fig...
Elementary Statistics (13th Edition)
Knowledge Booster
Similar questions
- Please help me answer this question!. Please handwrite it. I don't require AI answers. Thanks for your time!.arrow_forward1 What is the area of triangle ABC? 12 60° 60° A D B A 6√√3 square units B 18√3 square units 36√3 square units D 72√3 square unitsarrow_forwardPar quel quadrilatère est-elle représentée sur ce besoin en perspective cavalièrearrow_forward
- -10 M 10 y 5 P -5 R 5 -5 Ο 10 N -10 Οarrow_forwardDescribe enlargement on map gridarrow_forward◆ Switch To Light Mode HOMEWORK: 18, 19, 24, 27, 29 ***Please refer to the HOMEWORK sheet from Thursday, 9/14, for the problems ****Please text or email me if you have any questions 18. Figure 5-35 is a map of downtown Royalton, showing the Royalton River running through the downtown area and the three islands (A, B, and C) connected to each other and both banks by eight bridges. The Down- town Athletic Club wants to design the route for a marathon through the downtown area. Draw a graph that models the layout of Royalton. FIGURE 5-35 North Royalton Royalton River South Royption 19. A night watchman must walk the streets of the Green Hills subdivision shown in Fig. 5-36. The night watch- man needs to walk only once along each block. Draw a graph that models this situation.arrow_forward
- Solve this question and check if my answer provided is correctarrow_forwardProof: LN⎯⎯⎯⎯⎯LN¯ divides quadrilateral KLMN into two triangles. The sum of the angle measures in each triangle is ˚, so the sum of the angle measures for both triangles is ˚. So, m∠K+m∠L+m∠M+m∠N=m∠K+m∠L+m∠M+m∠N=˚. Because ∠K≅∠M∠K≅∠M and ∠N≅∠L, m∠K=m∠M∠N≅∠L, m∠K=m∠M and m∠N=m∠Lm∠N=m∠L by the definition of congruence. By the Substitution Property of Equality, m∠K+m∠L+m∠K+m∠L=m∠K+m∠L+m∠K+m∠L=°,°, so (m∠K)+ m∠K+ (m∠L)= m∠L= ˚. Dividing each side by gives m∠K+m∠L=m∠K+m∠L= °.°. The consecutive angles are supplementary, so KN⎯⎯⎯⎯⎯⎯∥LM⎯⎯⎯⎯⎯⎯KN¯∥LM¯ by the Converse of the Consecutive Interior Angles Theorem. Likewise, (m∠K)+m∠K+ (m∠N)=m∠N= ˚, or m∠K+m∠N=m∠K+m∠N= ˚. So these consecutive angles are supplementary and KL⎯⎯⎯⎯⎯∥NM⎯⎯⎯⎯⎯⎯KL¯∥NM¯ by the Converse of the Consecutive Interior Angles Theorem. Opposite sides are parallel, so quadrilateral KLMN is a parallelogram.arrow_forwardQuadrilateral BCDE is similar to quadrilateral FGHI. Find the measure of side FG. Round your answer to the nearest tenth if necessary. BCDEFGHI2737.55arrow_forward
- An angle measures 70.6° more than the measure of its supplementary angle. What is the measure of each angle?arrow_forwardName: Date: Per: Unit 7: Geometry Homework 4: Parallel Lines & Transversals **This is a 2-page document! ** Directions: Classify each angle pair and indicate whether they are congruent or supplementary. 1 1.23 and 25 2. 24 and 28 3. 22 and 25 4. 22 and 28 5. 21 and 27 6. 22 and 26 Directions: Find each angle measure. 7. Given: wvm25-149 m21- 8. Given: mn: m1=74 mz2- m22- m.23- m23- mz4= V mz4= m25= m26- m26= m27- m27 m28- m48= 9. Given: a || b: m28 125 m2- 10. Given: xy: m22-22 m21- = mz2- m43- m3- mZA m24-> m. 5- m25- m26- m.26=> m2]=> m27= m28- 11. Given: rm2-29: m15-65 m2=> m29-> m3- m. 10- mc4= m25= m212- m.46- m213- mat- m214- m28- & Gina when (N) Things ALICE 2017arrow_forwardMatch each statement to the set of shapes that best describes them. 1. Similar triangles by SSS 2. Similar triangles by SAS 3. Similar triangles by AA 4. The triangles are not similar > U E 35° 89° S F 89° J 35° 94° G 52° 90° E K 52° Iarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning