Chapter 14.3, Problem 12WE

a.

To determine

To find: Whether distance is invariant under glide reflection.

Answer to Problem 12WE

Yes, distance is invariant under glide reflection.

Explanation of Solution

Given:

  $T:(x,y)\to (x\text{'},y\text{'})$

Concept Used:

A translation moves ("slides") an object a fixed distance in a given direction without changing its size or shape, and without turning it or flipping it. The original object is called the pre-image, and the translation is called the image. An invariant is a property of a mathematical object which remains unchanged, after operations or transformations of a certain type are applied to the objects.

Calculation:

As per the given problem

Translation $T:(x,y)\to (x\text{'},y\text{'})$

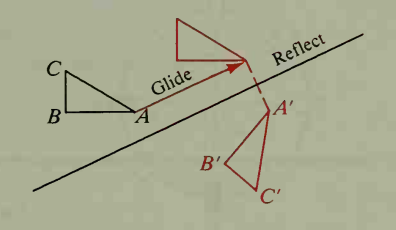
Distance between points is invariant under glide reflection.

i.e. $\begin{array}{l}AB=A\text{'}B\text{'}\\ BC=B\text{'}C\text{'}\\ CA=C\text{'}A\text{'}\end{array}$

Hence,

Distance is invariant under a glide reflection.

b.

To determine

To find: Whether angle measure is invariant under glide reflection.

Answer to Problem 12WE

Yes, angle measure is invariant under glide reflection.

Explanation of Solution

Given:

  $T:(x,y)\to (x\text{'},y\text{'})$

Concept Used:

A translation moves ("slides") an object a fixed distance in a given direction without changing its size or shape, and without turning it or flipping it. The original object is called the pre-image, and the translation is called the image. An invariant is a property of a mathematical object which remains unchanged, after operations or transformations of a certain type are applied to the objects.

Calculation:

As per the given problem

Translation $T:(x,y)\to (x\text{'},y\text{'})$

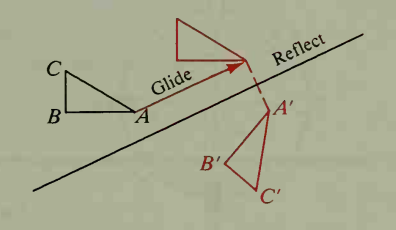
Angle measure between points is invariant under glide reflection.

i.e. $\begin{array}{l}\angle ABC=\angle A\text{'}B\text{'}C\text{'}\\ \angle BCA=\angle B\text{'}C\text{'}A\text{'}\\ \angle CAB=\angle C\text{'}A\text{'}B\text{'}\end{array}$

Hence,

Angle measure is invariant under a glide reflection.

c.

To determine

To find: Whether area is invariant under glide reflection.

Answer to Problem 12WE

Yes, area is invariant under glide reflection.

Explanation of Solution

Given:

  $T:(x,y)\to (x\text{'},y\text{'})$

Concept Used:

A translation moves ("slides") an object a fixed distance in a given direction without changing its size or shape, and without turning it or flipping it. The original object is called the pre-image, and the translation is called the image. An invariant is a property of a mathematical object which remains unchanged, after operations or transformations of a certain type are applied to the objects.

Calculation:

As per the given problem

Translation $T:(x,y)\to (x\text{'},y\text{'})$

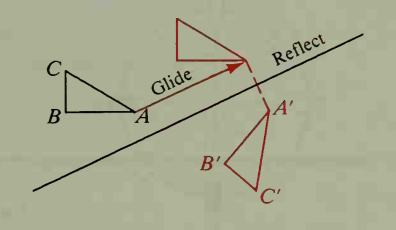
Area of polygon formed by points is invariant under glide reflection.

i.e. All the corresponding sides are equivalent & angle formed at all the points are same.

Hence,

Area is invariant under a glide reflection.

d.

To determine

To find: Whether orientation is invariant under glide reflection.

Answer to Problem 12WE

No, orientation is invariant under glide reflection.

Explanation of Solution

Given:

  $T:(x,y)\to (x\text{'},y\text{'})$

Concept Used:

A translation moves ("slides") an object a fixed distance in a given direction without changing its size or shape, and without turning it or flipping it. The original object is called the pre-image, and the translation is called the image. An invariant is a property of a mathematical object which remains unchanged, after operations or transformations of a certain type are applied to the objects. Orientation is how the relative pieces of an object are arranged.

Calculation:

As per the given problem

Translation $T:(x,y)\to (x\text{'},y\text{'})$

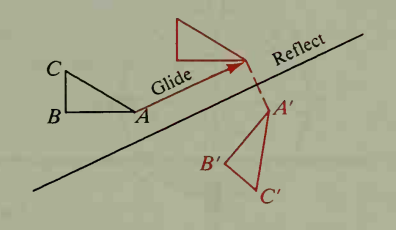
Slope of $BA$ changed after reflection to $B\text{'}A\text{'}$ .

Same for other sides as well. Reflection does not preserve orientation.

Hence,

Orientation is not invariant under a glide reflection.