Chapter 14.4, Problem 25WE

a.

To determine

To find: Distance invariant under half-turn.

Answer to Problem 25WE

Distance is invariant under a half-turn.

Explanation of Solution

Given:

Half-turn rotation

Concept Used:

A rotation is a transformation suggested by rotating a paddle wheel. When wheel stops, new position of a paddle referred as the image of initial position.

Invariant a function, quantity, or property which remains unchanged when a specified transformation is applied.

Calculation:

As per the given problem

There is a half-turn rotation.

For reference,

  

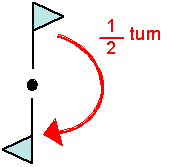
From diagram it can be understand that distance between the points i.e. triangle side length remains same.

Hence,

Distance is invariant under a half-turn.

b.

To determine

To find: Angle measure invariant under half-turn.

Answer to Problem 25WE

Angle measure is invariant under a half-turn.

Explanation of Solution

Given:

Half-turn rotation

Concept Used:

A rotation is a transformation suggested by rotating a paddle wheel. When wheel stops, new position of a paddle referred as the image of initial position.

Invariant a function, quantity, or property which remains unchanged when a specified transformation is applied.

Calculation:

As per the given problem

There is a half-turn rotation.

For reference,

  

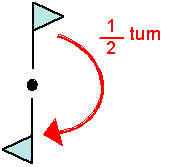
From diagram it can be understand that angle measure between the points i.e. triangle side angle remains same.

Hence,

Angle measure is invariant under a half-turn.

c.

To determine

To find: Area invariant under half-turn.

Answer to Problem 25WE

Area is invariant under a half-turn.

Explanation of Solution

Given:

Half-turn rotation

Concept Used:

A rotation is a transformation suggested by rotating a paddle wheel. When wheel stops, new position of a paddle referred as the image of initial position.

Invariant a function, quantity, or property which remains unchanged when a specified transformation is applied.

Calculation:

As per the given problem

There is a half-turn rotation.

For reference,

  

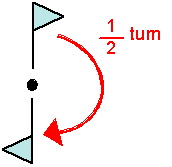
From diagram it can be understand that area between the points i.e. triangle area remains same.

Hence,

Area is invariant under a half-turn.

d.

To determine

To find: Orientation invariant under half-turn.

Answer to Problem 25WE

Orientation is not invariant under a half-turn.

Explanation of Solution

Given:

Half-turn rotation

Concept Used:

A rotation is a transformation suggested by rotating a paddle wheel. When wheel stops, new position of a paddle referred as the image of initial position.

Invariant a function, quantity, or property which remains unchanged when a specified transformation is applied.

Calculation:

As per the given problem

There is a half-turn rotation.

For reference,

  

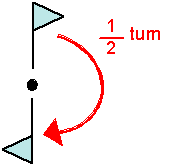
From diagram it can be understand that orientation of shape changes i.e. triangle face opposite to the previous orientation.

Hence,

Orientation is not invariant under a half-turn.