
To prove: that you can see all of yourself in a mirror that is only half as tall as you are.
Explanation of Solution
Given information:
The given statement is you can see all of yourself in a mirror that is only half as tall as you are.
Proof:
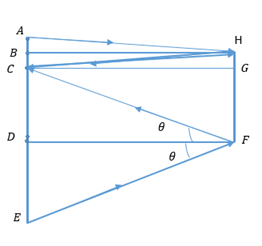
Consider you are standing in front of a mirror of height FH and your height is AE .
Point C represents your eye, A represents top of your head, E represents foot, B is the mid-point between your eye and top of your head, D is the mid-point between your eye and foot, F is the bottom of the mirror, H is the top of the mirror and G is a point in the mirror parallel to your eyes.
Since,
In similar
In similar triangles BCH and CGH
Substitute the values of HG and GF in equation i.
Therefore,
It is proved thatyou can see all of yourself in a mirror that is only half as tall as you are.
Chapter 14 Solutions
McDougal Littell Jurgensen Geometry: Student Edition Geometry
Additional Math Textbook Solutions
University Calculus: Early Transcendentals (4th Edition)
Calculus: Early Transcendentals (2nd Edition)
College Algebra (7th Edition)
Elementary Statistics: Picturing the World (7th Edition)
Elementary Statistics (13th Edition)
Algebra and Trigonometry (6th Edition)
- Find mSWarrow_forwardSelect all solids for which the formula V = Bh applies. A. a triangular prism B. a triangular pyramid C. a square pyramid D. a rectangular prism E. a cone F. a cylinderarrow_forwardThis is my h/w ,Required to find the region of shaded sector ,I don't really know how to deal with this tasks ,so if someone could help me to understand them it would be awesome,and sorry for my poor Englisharrow_forward
- △DEF△DEF has vertices D(0, 2) and F(6, 2). If △DEF△DEF has an area of 12 square units, select all the possible coordinates for E.arrow_forwardIn quadrilateral QRST, m<R=60, m<T=90, QR=RS, ST=8, TQ=8 How long is the longer diagonal of QRST? Find the ratio of RT to QS.arrow_forward13:26 ... ← Robert F. Blitzer - Thinkin... 0,04 61 KB/d 目 polygons to create a fraudulent tessellation with discrepancies that are too subtle for the eye to notice. In Exercises 45-46, you will use mathematics, not your eyes, to observe the irregularities. B A 45. Find the sum of the angle measures at vertex A. Then explain why the tessellation is a fake. 46. Find the sum of the angle measures at vertex B. Then explain why the tessellation is a fake. =et at If se Fic SECTION 10.3 Polygons, Perimeter, and Tessellations 645 61. I find it helpful to think of a polygon's perimeter as the length of its boundary. 62. If a polygon is not regular, I can determine the sum of the measures of its angles, but not the measure of any one of its angles. 63. I used floor tiles in the shape of regular pentagons to completely cover my kitchen floor. In Exercises 64-65, write an algebraic expression that represents the perimeter of the figure shown. is be 64. le a b C 2/ If se nyarrow_forward
- Schoology → C Cportsk12.com bookmarks Sis Grades and Attendance Al Detector - the Original Al Che X GPTZero + portsmouth.schoology.com/common-assessment-delivery/start/7747152192?action=onresume&submissionId=1600790102 New Tab Home | Schoology Quadrilateral Quiz English If WXYZ is a square, and WY = 32, find XY. Round your answer to the nearest tenth. Z XY = R X Y POSSIBLE POINTS: 5 2 of 20 48 21 1 2 345678910 Next ▸ Δ ㄖㄨ All Bookmarks Schoology Help Center | PRIVACY POLICY | Terms of Use PowerSchool ©2025arrow_forwardom nearest tenth if necessary. milsum 3. છે. 9.3mm 3mm A 78-43-92 4-3) 11.7 of 72.04-11.7-= lygons 7.8 mi 60.94 blants" 9 om 6. 4.15-7 16- 32m 1.8m 4.5m % ose 4.5m as to 65m 14 represents 5 square meters.arrow_forwardThe diagonals of rhombus ABCD intersect at E. Given that BAC=53 degrees, DE=8, and EC=6 find AEarrow_forward
- Volume of Dubai Cayan Towerarrow_forward1 B-P P+1+ 2-p 4-p min(Red)=? y=x² A (P,P')arrow_forwardMI P X /courses/segura10706/products/171960/pages/611?locale=&platformId=1030&lms=Y ☆ Finish Part I: Mathematics for Elementary and Middle School Teachers Continue in the app JJ 576 Chapter 12. Area of Shapes 9. Determine the area of the shaded shapes in Figure 12.48. Explain your reasoning. 1 unit S Figure 12.48 1 unit unit and the yarn for thearrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

