
Concept explainers
(a)
To Find:City has greater range of temperature
(a)
Answer to Problem 9PPS
Antelope has higher range than Augusta
Explanation of Solution
Given:The table shows the average monthly temperatures.
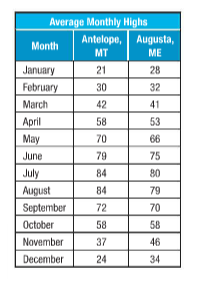
Which city has greater range of temperature?
Finding range
For Antelope MT
Highest vale =
Lowest value =
Range = Highest value − lowest value
For Augusta
Highest vale =
Lowest value =
Range = Highest value − lowest value
Hence, Antelope has higher range than Augusta
(b)
To Find:Measure of variation for each city
(b)
Answer to Problem 9PPS
For Antelope
Median =
Lower quartile
Upper quartile
Interquartile range
For Augusta
Median =
Lower quartile
Upper quartile
Interquartile range
Explanation of Solution
Given:The table shows the average monthly temperatures.
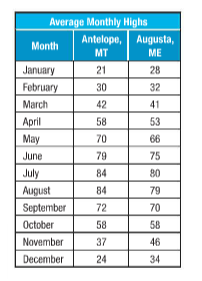
Find the measure of variation for each city.
For Antelope After arranging the data in ascending order
Median =
Lower quartile
Upper quartile
Interquartile range = Upper quartile − lower quartile
For Augusta After arranging the data in ascending order
Median =
Lower quartile
Upper quartile
Interquartile range = Upper quartile − lower quartile
(c)
To Compare:Medians and the interquartile ranges of average temperatures
(c)
Answer to Problem 9PPS
Median and interquartile range both of Antelope is greater than Augusta
Explanation of Solution
Given:The table shows the average monthly temperatures.
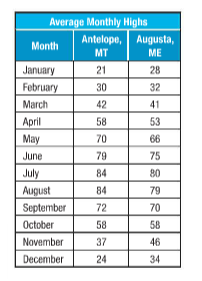
Compare the medians and the interquartile ranges of average temperatures.
For Antelope
Median =
Interquartile range
For Augusta
Median =
Interquartile range
It is concluded that Median and interquartile range both of Antelope is greater than Augusta
(d)
To Find:The appropriate measure of central tendency to describe the average high temperature for Augusta.
(d)
Answer to Problem 9PPS
Mean
Explanation of Solution
Given: The table shows the average monthly temperatures.
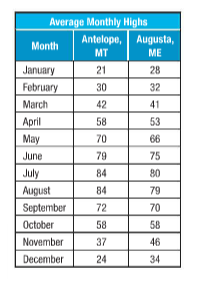
Select the appropriate measure of central tendency to describe the average high temperature for Augusta. Justify your response.
Mean is theappropriate measure of central tendency to describe the average high temperature for Augusta.
Because the range of values are large.
(e)
To Describe:Average temperatures of Antelope and Augusta.
(e)
Answer to Problem 9PPS
The average temperature of Antelope MT is higher than Augusta ME
Explanation of Solution
Given:The table shows the average monthly temperatures.
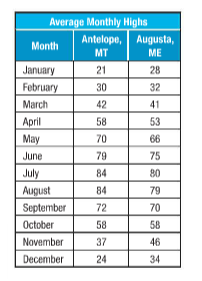
Describe the average temperatures of Antelope and Augusta using both the measures of central tendency and variation.
Measures of Central tendency
For Antelope
Mean
Median=
Mode =
For Augusta
Mean
Median=
No Mode
It is concluded that the average temperature of Antelope MT is higher than Augusta ME.
Measures of variation
For Antelope
Median =
Range=
Interquartile range
For Augusta
Median =
Range
Interquartile range
In the measures of variation the average temperature in Antelope is higher than Augusta.
Chapter 13 Solutions
Pre-Algebra, Student Edition
Additional Math Textbook Solutions
Basic Business Statistics, Student Value Edition
Elementary Statistics
College Algebra with Modeling & Visualization (5th Edition)
Intro Stats, Books a la Carte Edition (5th Edition)
Calculus: Early Transcendentals (2nd Edition)
- Evaluate the following expression and show your work to support your calculations. a). 6! b). 4! 3!0! 7! c). 5!2! d). 5!2! e). n! (n - 1)!arrow_forwardAmy and Samiha have a hat that contains two playing cards, one ace and one king. They are playing a game where they randomly pick a card out of the hat four times, with replacement. Amy thinks that the probability of getting exactly two aces in four picks is equal to the probability of not getting exactly two aces in four picks. Samiha disagrees. She thinks that the probability of not getting exactly two aces is greater. The sample space of possible outcomes is listed below. A represents an ace, and K represents a king. Who is correct?arrow_forwardConsider the exponential function f(x) = 12x. Complete the sentences about the key features of the graph. The domain is all real numbers. The range is y> 0. The equation of the asymptote is y = 0 The y-intercept is 1arrow_forward
- The graph shows Alex's distance from home after biking for x hours. What is the average rate of change from -1 to 1 for the function? 4-2 о A. -2 О B. 2 О C. 1 O D. -1 ty 6 4 2 2 0 X 2 4arrow_forwardWrite 7. √49 using rational exponents. ○ A. 57 47 B. 7 O C. 47 ○ D. 74arrow_forwardCan you check If my short explantions make sense because I want to make sure that I describe this part accuratelyarrow_forward
- 9! is 362, 880. What is 10!?arrow_forwardBruce and Krista are going to buy a new furniture set for their living room. They want to buy a couch, a coffee table, and a recliner. They have narrowed it down so that they are choosing between \[4\] couches, \[5\] coffee tables, and \[9\] recliners. How many different furniture combinations are possible?arrow_forwardCan you check if my step is correct?arrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





