Chapter 12.4, Problem 39E

(a)

To determine

To find: the limit of f when t approaches in infinity.

Answer to Problem 39E

The limit of the function approaches 1 when t approaches infinity.

Explanation of Solution

Given information:

The function $f\left(t\right)$ measures the level of oxygen in a pond at week t, where $f\left(t\right)=1$ is the normal level when $t=0$ .

The level of oxygen is $f\left(t\right)=\frac{t^2-t+1}{t^2+1}$ ,

Calculation:

It is given that the level of oxygen is $f\left(t\right)=\frac{t^2-t+1}{t^2+1}$ .

The limit of the function as x approaches infinity.

  $\begin{array}{c}\underset{t\to \infty }{\lim }f\left(t\right)=\underset{t\to \infty }{\lim }\frac{t^2-t+1}{t^2+1}\\ =\underset{t\to \infty }{\lim }\frac{t^2\left(1-\frac{t}{t^2}+\frac{1}{t^2}\right)}{t^2\left(1+\frac{1}{t^2}\right)}\\ =\underset{t\to \infty }{\lim }\frac{1-\frac{t}{t^2}+\frac{1}{t^2}}{1+\frac{1}{t^2}}\\ =\frac{\underset{t\to \infty }{\lim }1-\underset{t\to \infty }{\lim }\frac{1}{t}+\underset{t\to \infty }{\lim }\frac{1}{t^2}}{\underset{t\to \infty }{\lim }1+\underset{t\to \infty }{\lim }\frac{1}{t^2}}\end{array}$

If t approaches infinity, then $\frac{1}{t},\text{ and }\frac{1}{t^2}$ approaches infinity.

  $\begin{array}{c}\underset{t\to \infty }{\lim }f\left(t\right)=\frac{1-0+0}{1+0}\\ =1\end{array}$

Therefore, the limit of the function approaches 1 when t approaches infinity.

(b)

To determine

To sketch: the graphs of the function f and verify the result of part (a).

Explanation of Solution

Graph:

The graph of the function f as shown in Figure 1.

  

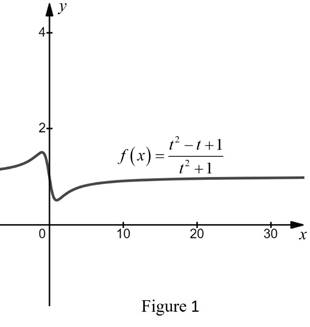
Interpretation:

From Figure 1, it is observed that the value of the function f approaches 1 whenever x is larger and large.

That is, the limit of the function f is 1 as x approaches infinity.

(c)

To determine

To explain: the meaning of the limit in context of the problem.

Answer to Problem 39E

The level of oxygens gets normal level over the long period of time.

Explanation of Solution

Interpretation:

In the context of the problem, the value of the function $f\left(t\right)=\frac{t^2-t+1}{t^2+1}$ approaches 1 as t approaches infinity.

Here, the function $f\left(t\right)=\frac{t^2-t+1}{t^2+1}$ represents the level of oxygens in a pond at week t.

It is given in the problem that $f\left(t\right)=1$ is the normal (unpolluted) level.

The term $\underset{t\to \infty }{\lim }f\left(t\right)=1$ means that the level of oxygens gets normal level over the long period of time.

Therefore, the level of oxygens gets normal level over the long period of time.