
Concept explainers
(a)
To sketch: the graph of the function
(a)
Explanation of Solution
Graph:
The graph of the function
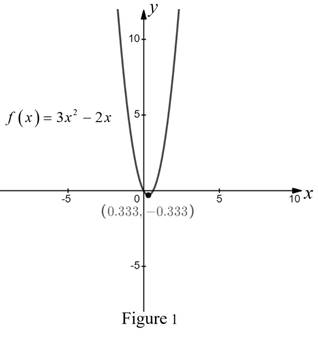
Interpretation:
From Figure 1, it is observed that the shape of the function f is parabola open upward.
(b)
To find: the coordinates of the vertex of the parabola
(b)
Answer to Problem 78E
The coordinates of the vertex of the parabola are
Explanation of Solution
Interpretation:
From Figure 1, it is observed that the parabola is upward open.
Note that, the minimum value of the upward open parabola is vertex point.
The function
The minimum value of
Therefore, the vertex of the parabola is
Hence, the coordinates of the vertex of the parabola are
(c)
To find: the slope of the tangent of function
(c)
Answer to Problem 78E
The slope of the tangent of function f at vertex is 0.
Explanation of Solution
Calculation:
From part (a), the derivative of the function
Note that, the slope of the tangent of the graph of the function
The slope of the tangent of function
Substitute
Therefore, the slope of the tangent of function f at vertex is 0.
(d)
To make: the conjecture about the slope of the tangent line at the vertex of an arbitrary parabola.
(d)
Answer to Problem 78E
The slope of the tangent line at vertex of the any parabola is zero.
Explanation of Solution
Interpretation:
From part (c), the slope of the tangent line of the parabola at vertex is zero.
The vertex point is a minimum point of upward open parabola and maximum point of downward open parabola. Also, the vertex point is a turning point only it never gets sharp nose.
The tangent of the vertex point is horizontal line and the slope of the horizontal line is zero.
Therefore, the slope of the tangent line at vertex of the any parabola is zero.
Chapter 12 Solutions
EBK PRECALCULUS W/LIMITS
- Find the equation of the line / in the figure below. Give exact values using the form y = mx + b. m = b = y WebAssign Plot f(x) = 10* log 9 Xarrow_forwardA particle travels along a straight line path given by s=9.5t3-2.2t2-4.5t+9.9 (in meters). What time does it change direction? Report the higher of the answers to the nearest 2 decimal places in seconds.arrow_forwardUse the method of disks to find the volume of the solid that is obtained when the region under the curve y = over the interval [4,17] is rotated about the x-axis.arrow_forward
- 1. Find the area of the region enclosed between the curves y = x and y = x. Sketch the region.arrow_forwardfor the given rectangular coordinates, find two sets of polar coordinates for which 0≤θ<2π, one with r>0 and the other with r<0. (-2sqrt(3),9)arrow_forwardI circled the correct answer, could you show me how to do it using divergence and polar coordinatesarrow_forward
- The correct answer is D Could you explain and show the steps pleasearrow_forwardTaylor Series Approximation Example- H.W More terms used implies better approximation f(x) 4 f(x) Zero order f(x + 1) = f(x;) First order f(x; + 1) = f(x;) + f'(x;)h 1.0 Second order 0.5 True f(x + 1) = f(x) + f'(x)h + ƒ"(x;) h2 2! f(x+1) 0 x; = 0 x+1 = 1 x h f(x)=0.1x4-0.15x³- 0.5x2 -0.25x + 1.2 51 Taylor Series Approximation H.w: Smaller step size implies smaller error Errors f(x) + f(x,) Zero order f(x,+ 1) = f(x) First order 1.0 0.5 Reduced step size Second order True f(x + 1) = f(x) + f'(x)h f(x; + 1) = f(x) + f'(x)h + "(xi) h2 f(x,+1) O x₁ = 0 x+1=1 Using Taylor Series Expansion estimate f(1.35) with x0 =0.75 with 5 iterations (or & s= 5%) for f(x)=0.1x 0.15x³-0.5x²- 0.25x + 1.2 52arrow_forwardCould you explain this using the formula I attached and polar coorindatesarrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





