Chapter 12, Problem 38RE

a

To determine

Graph the function by using a graphing utility.

Answer to Problem 38RE

The function converges to a single bounded valve as it approaches $4$ from both sides left and right

Explanation of Solution

Given information:

Graphically approximate the limit (if it exists) by using a graphing utility to graph the function.

  $\underset{x\to 4}{\lim }\frac{4-x}{16-x^2}$

Calculation:

The limit of given function is,

  $\underset{x\to 4}{\lim }\frac{4-x}{16-x^2}$

Let plot the given function.

To calculate the model graphically use graphic utility TI-83calculator,

Press Y key and enter the equation,

  

Press zoom and 0: zoom fit,

  

Now plot window,

  

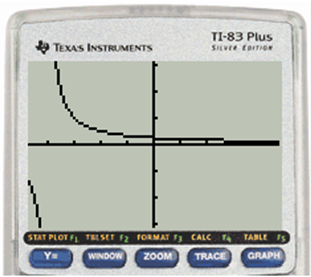
From the graph we observe that the function converges to a single bounded valve as it approaches $4$ from both sides left and right.

Hence the function converges to a single bounded valve as it approaches $4$ from both sides left and right

b

To determine

Create a table by using the table feature of the graphing utility.

Answer to Problem 38RE

Limit converges to value $\boxed{0.125}$

Explanation of Solution

Given information:

Numerically approximate the limit (if it exists) by using the table feature of the graphing utility to create a table.

  $\underset{x\to 4}{\lim }\frac{4-x}{16-x^2}$

Calculation:

Numerically approximate the limit using $f\left(x\right)=\frac{4-x}{16-x^2}$ and tabulate it using the TI-83 graphing calculator,

Press Y key and enter the equation,

  

Press 2^nd key and window to set table.

  

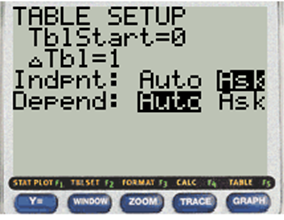
Press 2^nd key and graph button to enter the value of $x$ .

  

Hence limit converges to value $\boxed{0.125}$