Student Solutions Manual, Single Variable for Calculus: Early Transcendentals
Student Solutions Manual, Single Variable for Calculus: Early Transcendentals
2nd Edition
ISBN: 9780321954329
Author: William L. Briggs, Lyle Cochran, Bernard Gillett
Publisher: PEARSON
bartleby

Concept explainers

Optimization
Optimization comes from the same root as "optimal". "Optimal" means the highest. When you do the optimization process, that is when you are "making it best" to maximize everything and to achieve optimal results, a set of parameters is the base for the se…
Integration
Integration means to sum the things. In mathematics, it is the branch of Calculus which is used to find the area under the curve. The operation subtraction is the inverse of addition, division is the inverse of multiplication. In the same way, integratio…
Application of Integration
In mathematics, the process of integration is used to compute complex area related problems. With the application of integration, solving area related problems, whether they are a curve, or a curve between lines, can be done easily.
Volume
In mathematics, we describe the term volume as a quantity that can express the total space that an object occupies at any point in time. Usually, volumes can only be calculated for 3-dimensional objects. By 3-dimensional or 3D objects, we mean objects th…
Area
Area refers to the amount of space a figure encloses and the number of square units that cover a shape. It is two-dimensional and is measured in square units.
bartleby

Videos

Textbook Question
Book Icon
Chapter 12, Problem 83RE

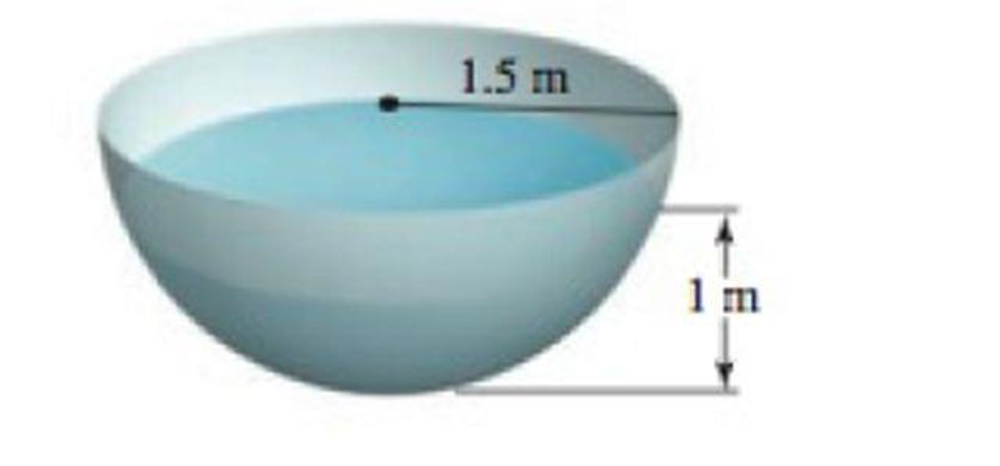
Water-level changes A hemispherical tank with a radius of 1.50 m is filled with water to a depth of 1.00 m. Water is released from the tank and the water level drops by 0.05 m (from 1.00 m to 0.95 m).

a.    Approximate the change in the volume of water in the tank. The volume of a spherical cap is V = πh2(3r – h)/3, where r is the radius of the sphere and h is the thickness of the cap (in this case, the depth of the water).

b.    Approximate the change in the surface area of the water in the tank.

Chapter 12, Problem 83RE, Water-level changes A hemispherical tank with a radius of 1.50 m is filled with water to a depth of

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 12, Problem 82RE
Next
Chapter 12, Problem 84RE
Students have asked these similar questions
1/ Solve the following: 1 x + X + cos(3X) -75 -1 2 2 (5+1) e 5² + 5 + 1 3 L -1 1 5² (5²+1) 1 5(5-5)
I need expert handwritten solution.to this integral
How to understand and learn Laurent's serial and what's the point of Laurent's serial And what are the steps of a smooth solution for Laurent

Chapter 12 Solutions

Student Solutions Manual, Single Variable for Calculus: Early Transcendentals

Ch. 12.1 - Give two pieces of information which, taken...Ch. 12.1 - Find a vector normal to the plane 2x 3y + 4z =...Ch. 12.1 - Where does the plane 2x 3y + 4z = 12 intersect...Ch. 12.1 - Give an equation of the plane with a normal vector...Ch. 12.1 - To which coordinate axes are the following...Ch. 12.1 - Describe the graph of x = z2 in 3.Ch. 12.1 - What is a trace of a surface?Ch. 12.1 - What is the name of the surface defined by the...Ch. 12.1 - What is the name of the surface defined by the...Ch. 12.1 - What is the name of the surface defined by the...
Ch. 12.1 - Equations of planes Find an equation of the plane...Ch. 12.1 - Prob. 12ECh. 12.1 - Equations of planes Find an equation of the plane...Ch. 12.1 - Equations of planes Find an equation of the plane...Ch. 12.1 - Equation of a plane Find an equation of the plane...Ch. 12.1 - Equation of a plane Find an equation of the plane...Ch. 12.1 - Equations of planes Find an equation of the...Ch. 12.1 - Equations of planes Find an equation of the...Ch. 12.1 - Equations of planes Find an equation of the...Ch. 12.1 - Equations of planes Find an equation of the...Ch. 12.1 - Properties of planes Find the points at which the...Ch. 12.1 - Prob. 22ECh. 12.1 - Properties of planes Find the points at which the...Ch. 12.1 - Prob. 24ECh. 12.1 - Pairs of planes Determine whether the following...Ch. 12.1 - Pairs of planes Determine whether the following...Ch. 12.1 - Pairs of planes Determine whether the following...Ch. 12.1 - Pairs of planes Determine whether the following...Ch. 12.1 - Equations of planes For the following sets of...Ch. 12.1 - Equations of planes For the following sets of...Ch. 12.1 - Parallel planes Find an equation of the plane...Ch. 12.1 - Prob. 32ECh. 12.1 - Prob. 33ECh. 12.1 - Prob. 34ECh. 12.1 - Intersecting planes Find an equation of the line...Ch. 12.1 - Intersecting planes Find an equation of the line...Ch. 12.1 - Intersecting planes Find an equation of the line...Ch. 12.1 - Intersecting planes Find an equation of the line...Ch. 12.1 - Cylinders in 3 Consider the following cylinders in...Ch. 12.1 - Cylinders in 3 Consider the following cylinders in...Ch. 12.1 - Cylinders in 3 Consider the following cylinders in...Ch. 12.1 - Cylinders in 3 Consider the following cylinders in...Ch. 12.1 - Cylinders in 3 Consider the following cylinders in...Ch. 12.1 - Cylinders in 3 Consider the following cylinders in...Ch. 12.1 - Cylinders in 3 Consider the following cylinders in...Ch. 12.1 - Cylinders in 3 Consider the following cylinders in...Ch. 12.1 - Quadric surfaces Consider the following equations...Ch. 12.1 - Quadric surfaces Consider the following equations...Ch. 12.1 - Quadric surfaces Consider the following equations...Ch. 12.1 - Quadric surfaces Consider the following equations...Ch. 12.1 - Quadric surfaces Consider the following equations...Ch. 12.1 - Quadric surfaces Consider the following equations...Ch. 12.1 - Quadric surfaces Consider the following equations...Ch. 12.1 - Prob. 54ECh. 12.1 - Quadric surfaces Consider the following equations...Ch. 12.1 - Quadric surfaces Consider the following equations...Ch. 12.1 - Quadric surfaces Consider the following equations...Ch. 12.1 - Prob. 58ECh. 12.1 - Quadric surfaces Consider the following equations...Ch. 12.1 - Quadric surfaces Consider the following equations...Ch. 12.1 - Quadric surfaces Consider the following equations...Ch. 12.1 - Quadric surfaces Consider the following equations...Ch. 12.1 - Quadric surfaces Consider the following equations...Ch. 12.1 - Prob. 64ECh. 12.1 - Prob. 65ECh. 12.1 - Prob. 66ECh. 12.1 - Quadric surfaces Consider the following equations...Ch. 12.1 - Prob. 68ECh. 12.1 - Quadric surfaces Consider the following equations...Ch. 12.1 - Quadric surfaces Consider the following equations...Ch. 12.1 - Explain why or why not Determine whether the...Ch. 12.1 - Prob. 72ECh. 12.1 - Lines normal to planes Find an equation of the...Ch. 12.1 - Lines normal to planes Find an equation of the...Ch. 12.1 - Prob. 75ECh. 12.1 - Orthogonal plane Find an equation of the plane...Ch. 12.1 - Three intersecting planes Describe the set of all...Ch. 12.1 - Three intersecting planes Describe the set of all...Ch. 12.1 - Matching graphs with equations Match equations af...Ch. 12.1 - Identifying surfaces Identify and briefly describe...Ch. 12.1 - Identifying surfaces Identify and briefly describe...Ch. 12.1 - Identifying surfaces Identify and briefly describe...Ch. 12.1 - Identifying surfaces Identify and briefly describe...Ch. 12.1 - Identifying surfaces Identify and briefly describe...Ch. 12.1 - Identifying surfaces Identify and briefly describe...Ch. 12.1 - Identifying surfaces Identify and briefly describe...Ch. 12.1 - Identifying surfaces Identify and briefly describe...Ch. 12.1 - Identifying surfaces Identify and briefly describe...Ch. 12.1 - Identifying surfaces Identify and briefly describe...Ch. 12.1 - Prob. 90ECh. 12.1 - Prob. 91ECh. 12.1 - Prob. 92ECh. 12.1 - Prob. 93ECh. 12.1 - Prob. 94ECh. 12.1 - Angle between planes The angle between two planes...Ch. 12.1 - Prob. 96ECh. 12.1 - Light cones The idea of a light cone appears in...Ch. 12.1 - Prob. 100ECh. 12.1 - Prob. 102ECh. 12.1 - Prob. 103ECh. 12.1 - Prob. 104ECh. 12.2 - What is domain of f(x, y) = x2y xy2?Ch. 12.2 - What is the domain of g(x, y) = 1/(xy)?Ch. 12.2 - What is the domain of h(x,y)=xy?Ch. 12.2 - How many axes (or how many dimensions) are needed...Ch. 12.2 - Explain how to graph the level curves of a surface...Ch. 12.2 - Describe in words the level curves of the...Ch. 12.2 - How many axes (or how many dimensions) are needed...Ch. 12.2 - The domain of Q = f(u, v, w, x, y, z) lies in n...Ch. 12.2 - Give two methods for graphically representing a...Ch. 12.2 - Domains Find the domain of the following...Ch. 12.2 - Prob. 12ECh. 12.2 - Domains Find the domain of the following...Ch. 12.2 - Domains Find the domain of the following...Ch. 12.2 - Domains Find the domain of the following...Ch. 12.2 - Domains Find the domain of the following...Ch. 12.2 - Domains Find the domain of the following...Ch. 12.2 - Domains Find the domain of the following...Ch. 12.2 - Domains Find the domain of the following...Ch. 12.2 - Domains Find the domain of the following...Ch. 12.2 - Graphs of familiar functions Use what you learned...Ch. 12.2 - Graphs of familiar functions Use what you learned...Ch. 12.2 - Graphs of familiar functions Use what you learned...Ch. 12.2 - Graphs of familiar functions Use what you learned...Ch. 12.2 - Graphs of familiar functions Use what you learned...Ch. 12.2 - Graphs of familiar functions Use what you learned...Ch. 12.2 - Graphs of familiar functions Use what you learned...Ch. 12.2 - Prob. 28ECh. 12.2 - Matching surfaces Match functions ad with surfaces...Ch. 12.2 - Level curves Graph several level curves of the...Ch. 12.2 - Level curves Graph several level curves of the...Ch. 12.2 - Level curves Graph several level curves of the...Ch. 12.2 - Level curves Graph several level curves of the...Ch. 12.2 - Level curves Graph several level curves of the...Ch. 12.2 - Level curves Graph several level curves of the...Ch. 12.2 - Level curves Graph several level curves of the...Ch. 12.2 - Level curves Graph several level curves of the...Ch. 12.2 - Matching level curves with surfaces Match surfaces...Ch. 12.2 - Prob. 39ECh. 12.2 - Earned run average A baseball pitchers earned run...Ch. 12.2 - Electric potential function The electric potential...Ch. 12.2 - Cobb-Douglas production function The output Q of...Ch. 12.2 - Resistors in parallel Two resistors wired in...Ch. 12.2 - Water waves A snapshot of a water wave moving...Ch. 12.2 - Approximate mountains Suppose the elevation of...Ch. 12.2 - Domains of functions of three or more variables...Ch. 12.2 - Domains of functions of three or more variables...Ch. 12.2 - Domains of functions of three or more variables...Ch. 12.2 - Domains of functions of three or more variables...Ch. 12.2 - Domains of functions of three or more variables...Ch. 12.2 - Domains of functions of three or more variables...Ch. 12.2 - Prob. 52ECh. 12.2 - Explain why or why not Determine whether the...Ch. 12.2 - Graphing functions a.Determine the domain and...Ch. 12.2 - Prob. 55ECh. 12.2 - Prob. 56ECh. 12.2 - Graphing functions a.Determine the domain and...Ch. 12.2 - Graphing functions a.Determine the domain and...Ch. 12.2 - Prob. 59ECh. 12.2 - Prob. 60ECh. 12.2 - Prob. 61ECh. 12.2 - Prob. 62ECh. 12.2 - Peaks and valleys The following functions have...Ch. 12.2 - Prob. 64ECh. 12.2 - Prob. 65ECh. 12.2 - Level surfaces Find an equation for the family of...Ch. 12.2 - Level surfaces Find an equation for the family of...Ch. 12.2 - Level surfaces Find an equation for the family of...Ch. 12.2 - Level surfaces Find an equation for the family of...Ch. 12.2 - Level curves of a savings account Suppose you make...Ch. 12.2 - Level curves of a savings plan Suppose you make...Ch. 12.2 - Prob. 72ECh. 12.2 - Ideal Gas Law Many gases can be modeled by the...Ch. 12.2 - Prob. 74ECh. 12.2 - Challenge domains Find the domains of the...Ch. 12.2 - Prob. 76ECh. 12.2 - Prob. 77ECh. 12.2 - Prob. 78ECh. 12.3 - Prob. 1ECh. 12.3 - Explain why f(x, y) must approach a unique number...Ch. 12.3 - What does it mean to say that limits of...Ch. 12.3 - Suppose (a, b) is on the boundary of the domain of...Ch. 12.3 - Explain how examining limits along multiple paths...Ch. 12.3 - Explain why evaluating a limit along a finite...Ch. 12.3 - What three conditions must be met for a function f...Ch. 12.3 - Let R be the unit disk {(x, y): x2 + y2 1} with...Ch. 12.3 - At what points of 2 is a rational function of two...Ch. 12.3 - Prob. 10ECh. 12.3 - Limits of functions Evaluate the following limits....Ch. 12.3 - Limits of functions Evaluate the following limits....Ch. 12.3 - Limits of functions Evaluate the following limits....Ch. 12.3 - Limits of functions Evaluate the following limits....Ch. 12.3 - Limits of functions Evaluate the following limits....Ch. 12.3 - Limits of functions Evaluate the following limits....Ch. 12.3 - Limits of functions Evaluate the following limits....Ch. 12.3 - Limits of functions Evaluate the following limits....Ch. 12.3 - Prob. 19ECh. 12.3 - Limits at boundary points Evaluate the following...Ch. 12.3 - Limits at boundary points Evaluate the following...Ch. 12.3 - Limits at boundary points Evaluate the following...Ch. 12.3 - Limits at boundary points Evaluate the following...Ch. 12.3 - Prob. 24ECh. 12.3 - Limits at boundary points Evaluate the following...Ch. 12.3 - Prob. 26ECh. 12.3 - Prob. 27ECh. 12.3 - Prob. 28ECh. 12.3 - Nonexistence of limits Use the Two-Path Test to...Ch. 12.3 - Prob. 30ECh. 12.3 - Nonexistence of limits Use the Two-Path Test to...Ch. 12.3 - Nonexistence of limits Use the Two-Path Test to...Ch. 12.3 - Continuity At what points of 2 are the following...Ch. 12.3 - Continuity At what points of 2 are the following...Ch. 12.3 - Continuity At what points of 2 are the following...Ch. 12.3 - Continuity At what points of 2 are the following...Ch. 12.3 - Continuity At what points of 2 are the following...Ch. 12.3 - Continuity At what points of 2 are the following...Ch. 12.3 - Continuity At what points of 2 are the following...Ch. 12.3 - Continuity At what points of 2 are the following...Ch. 12.3 - Continuity of composite functions At what points...Ch. 12.3 - Continuity of composite functions At what points...Ch. 12.3 - Continuity of composite functions At what points...Ch. 12.3 - Continuity of composite functions At what points...Ch. 12.3 - Continuity of composite functions At what points...Ch. 12.3 - Continuity of composite functions At what points...Ch. 12.3 - Continuity of composite functions At what points...Ch. 12.3 - Continuity of composite functions At what points...Ch. 12.3 - Continuity of composite functions At what points...Ch. 12.3 - Continuity of composite functions At what points...Ch. 12.3 - Continuity of composite functions At what points...Ch. 12.3 - Continuity of composite functions At what points...Ch. 12.3 - Limits of functions of three variables Evaluate...Ch. 12.3 - Limits of functions of three variables Evaluate...Ch. 12.3 - Limits of functions of three variables Evaluate...Ch. 12.3 - Limits of functions of three variables Evaluate...Ch. 12.3 - Limits of functions of three variables Evaluate...Ch. 12.3 - Limits of functions of three variables Evaluate...Ch. 12.3 - Prob. 59ECh. 12.3 - Miscellaneous limits Use the method of your choice...Ch. 12.3 - Miscellaneous limits Use the method of your choice...Ch. 12.3 - Miscellaneous limits Use the method of your choice...Ch. 12.3 - Prob. 63ECh. 12.3 - Miscellaneous limits Use the method of your choice...Ch. 12.3 - Miscellaneous limits Use the method of your choice...Ch. 12.3 - Prob. 66ECh. 12.3 - Miscellaneous limits Use the method of your choice...Ch. 12.3 - Prob. 68ECh. 12.3 - Prob. 69ECh. 12.3 - Prob. 70ECh. 12.3 - Prob. 71ECh. 12.3 - Prob. 72ECh. 12.3 - Piecewise function Let...Ch. 12.3 - Prob. 74ECh. 12.3 - Nonexistence of limits Show that...Ch. 12.3 - Prob. 76ECh. 12.3 - Limits of composite functions Evaluate the...Ch. 12.3 - Prob. 78ECh. 12.3 - Limits of composite functions Evaluate the...Ch. 12.3 - Limits of composite functions Evaluate the...Ch. 12.3 - Prob. 81ECh. 12.3 - Limit proof Use the formal definition of a limit...Ch. 12.3 - Limit proof Use the formal definition of a limit...Ch. 12.3 - Proof of Limit Law 1 Use the formal definition of...Ch. 12.3 - Proof of Limit Law 3 Use the formal definition of...Ch. 12.4 - Suppose you are standing on the surface z = f(x,...Ch. 12.4 - Prob. 2ECh. 12.4 - Prob. 3ECh. 12.4 - Prob. 4ECh. 12.4 - Prob. 5ECh. 12.4 - The volume of a right circular cylinder with...Ch. 12.4 - Prob. 7ECh. 12.4 - Prob. 8ECh. 12.4 - Prob. 9ECh. 12.4 - Prob. 10ECh. 12.4 - Prob. 11ECh. 12.4 - Prob. 12ECh. 12.4 - Prob. 13ECh. 12.4 - Prob. 14ECh. 12.4 - Prob. 15ECh. 12.4 - Prob. 16ECh. 12.4 - Prob. 17ECh. 12.4 - Prob. 18ECh. 12.4 - Prob. 19ECh. 12.4 - Prob. 20ECh. 12.4 - Prob. 21ECh. 12.4 - Prob. 22ECh. 12.4 - Prob. 23ECh. 12.4 - Prob. 24ECh. 12.4 - Prob. 25ECh. 12.4 - Prob. 26ECh. 12.4 - Prob. 27ECh. 12.4 - Prob. 28ECh. 12.4 - Prob. 29ECh. 12.4 - Prob. 30ECh. 12.4 - Prob. 31ECh. 12.4 - Prob. 32ECh. 12.4 - Prob. 33ECh. 12.4 - Prob. 34ECh. 12.4 - Prob. 35ECh. 12.4 - Prob. 36ECh. 12.4 - Prob. 37ECh. 12.4 - Prob. 38ECh. 12.4 - Prob. 39ECh. 12.4 - Prob. 40ECh. 12.4 - Prob. 41ECh. 12.4 - Prob. 42ECh. 12.4 - Prob. 43ECh. 12.4 - Equality of mixed partial derivatives Verify that...Ch. 12.4 - Prob. 45ECh. 12.4 - Prob. 46ECh. 12.4 - Prob. 47ECh. 12.4 - Prob. 48ECh. 12.4 - Prob. 49ECh. 12.4 - Prob. 50ECh. 12.4 - Prob. 51ECh. 12.4 - Prob. 52ECh. 12.4 - Prob. 53ECh. 12.4 - Prob. 54ECh. 12.4 - Gas law calculations Consider the Ideal Gas Law PV...Ch. 12.4 - Prob. 56ECh. 12.4 - Nondifferentiability? Consider the following...Ch. 12.4 - Nondifferentiability? Consider the following...Ch. 12.4 - Prob. 59ECh. 12.4 - Prob. 60ECh. 12.4 - Prob. 61ECh. 12.4 - Prob. 62ECh. 12.4 - Prob. 63ECh. 12.4 - Prob. 64ECh. 12.4 - Prob. 65ECh. 12.4 - Miscellaneous partial derivatives Compute the...Ch. 12.4 - Prob. 67ECh. 12.4 - Prob. 68ECh. 12.4 - Prob. 69ECh. 12.4 - Spherical caps The volume of the cap of a sphere...Ch. 12.4 - Prob. 71ECh. 12.4 - Body mass index The body mass index (BMI) for an...Ch. 12.4 - Electric potential function The electric potential...Ch. 12.4 - Prob. 74ECh. 12.4 - Resistors in parallel Two resistors in an...Ch. 12.4 - Wave on a string Imagine a string that is fixed at...Ch. 12.4 - Wave equation Traveling waves (for example, water...Ch. 12.4 - Wave equation Traveling waves (for example, water...Ch. 12.4 - Wave equation Traveling waves (for example, water...Ch. 12.4 - Laplaces equation A classical equation of...Ch. 12.4 - Laplaces equation A classical equation of...Ch. 12.4 - Laplaces equation A classical equation of...Ch. 12.4 - Laplaces equation A classical equation of...Ch. 12.4 - Heat equation The flow of hear along a thin...Ch. 12.4 - Heat equation The flow of hear along a thin...Ch. 12.4 - Prob. 86ECh. 12.4 - Heat equation The flow of hear along a thin...Ch. 12.4 - Prob. 88ECh. 12.4 - Differentiability Use the definition of...Ch. 12.4 - Nondifferentiability? Consider the following...Ch. 12.4 - Nondifferentiability? Consider the following...Ch. 12.4 - Prob. 92ECh. 12.4 - Derivatives of an integral Let h be continuous for...Ch. 12.4 - Prob. 94ECh. 12.4 - Prob. 95ECh. 12.5 - Suppose z = f(x, y), where x and y are functions...Ch. 12.5 - Let z be a function of x and y, while x and y are...Ch. 12.5 - Suppose w is a function of x, y and z, which are...Ch. 12.5 - Let z = f(x, y), x = g(s, t), and y = h(s, t)....Ch. 12.5 - Given that w = F(x, y, z), and x, y, and z are...Ch. 12.5 - Suppose F(x, y) = 0 and y is a differentiable...Ch. 12.5 - Chain Rule with one independent variable Use...Ch. 12.5 - Prob. 8ECh. 12.5 - Chain Rule with one independent variable Use...Ch. 12.5 - Chain Rule with one independent variable Use...Ch. 12.5 - Chain Rule with one independent variable Use...Ch. 12.5 - Prob. 12ECh. 12.5 - Chain Rule with one independent variable Use...Ch. 12.5 - Prob. 14ECh. 12.5 - Chain Rule with one independent variable Use...Ch. 12.5 - Chain Rule with one independent variable Use...Ch. 12.5 - Changing cylinder The volume of a right circular...Ch. 12.5 - Changing pyramid The volume of a pyramid with a...Ch. 12.5 - Chain Rule with several independent variables Find...Ch. 12.5 - Chain Rule with several independent variables Find...Ch. 12.5 - Chain Rule with several independent variables Find...Ch. 12.5 - Chain Rule with several independent variables Find...Ch. 12.5 - Chain Rule with several independent variables Find...Ch. 12.5 - Prob. 24ECh. 12.5 - Chain Rule with several independent variables Find...Ch. 12.5 - Prob. 26ECh. 12.5 - Making trees Use a tree diagram to write the...Ch. 12.5 - Prob. 28ECh. 12.5 - Prob. 29ECh. 12.5 - Prob. 30ECh. 12.5 - Implicit differentiation Given the following...Ch. 12.5 - Implicit differentiation Given the following...Ch. 12.5 - Implicit differentiation Given the following...Ch. 12.5 - Implicit differentiation Given the following...Ch. 12.5 - Implicit differentiation Given the following...Ch. 12.5 - Implicit differentiation Given the following...Ch. 12.5 - Prob. 37ECh. 12.5 - Prob. 38ECh. 12.5 - Prob. 39ECh. 12.5 - Derivative practice two ways Find the indicated...Ch. 12.5 - Derivative practice two ways Find the indicated...Ch. 12.5 - Derivative practice Find the indicated derivative...Ch. 12.5 - Derivative practice Find the indicated derivative...Ch. 12.5 - Derivative practice Find the indicated derivative...Ch. 12.5 - Derivative practice Find the indicated derivative...Ch. 12.5 - Prob. 46ECh. 12.5 - Change on a line Suppose w=(x,y,z) and is the line...Ch. 12.5 - Prob. 48ECh. 12.5 - Prob. 49ECh. 12.5 - Prob. 50ECh. 12.5 - Prob. 51ECh. 12.5 - Prob. 52ECh. 12.5 - Walking on a surface Consider the following...Ch. 12.5 - Walking on a surface Consider the following...Ch. 12.5 - Walking on a surface Consider the following...Ch. 12.5 - Walking on a surface Consider the following...Ch. 12.5 - Conservation of energy A projectile with mass m is...Ch. 12.5 - Utility functions in economics Economists use...Ch. 12.5 - Constant volume tori The volume of a solid torus...Ch. 12.5 - Body surface area One of several empirical...Ch. 12.5 - Prob. 61ECh. 12.5 - Prob. 62ECh. 12.5 - Prob. 63ECh. 12.5 - Change of coordinates Recall that Cartesian and...Ch. 12.5 - Change of coordinates continued An important...Ch. 12.5 - Prob. 67ECh. 12.5 - Prob. 68ECh. 12.5 - Prob. 69ECh. 12.6 - Prob. 1ECh. 12.6 - How do you compute the gradient of the functions...Ch. 12.6 - Prob. 3ECh. 12.6 - Prob. 4ECh. 12.6 - Given a function f, explain the relationship...Ch. 12.6 - The level curves of the surface z=x2+y2 are...Ch. 12.6 - Directional derivatives Consider the function...Ch. 12.6 - Directional derivatives Consider the function...Ch. 12.6 - Computing gradients Compute the gradient of the...Ch. 12.6 - Computing gradients Compute the gradient of the...Ch. 12.6 - Computing gradients Compute the gradient of the...Ch. 12.6 - Computing gradients Compute the gradient of the...Ch. 12.6 - Computing gradients Compute the gradient of the...Ch. 12.6 - Computing gradients Compute the gradient of the...Ch. 12.6 - Computing gradients Compute the gradient of the...Ch. 12.6 - Computing gradients Compute the gradient of the...Ch. 12.6 - Computing directional derivatives with the...Ch. 12.6 - Computing directional derivatives with the...Ch. 12.6 - Prob. 19ECh. 12.6 - Computing directional derivatives with the...Ch. 12.6 - Computing directional derivatives with the...Ch. 12.6 - Prob. 22ECh. 12.6 - Computing directional derivatives with the...Ch. 12.6 - Computing directional derivatives with the...Ch. 12.6 - Computing directional derivatives with the...Ch. 12.6 - Computing directional derivatives with the...Ch. 12.6 - Direction of steepest ascent and descent Consider...Ch. 12.6 - Direction of steepest ascent and descent Consider...Ch. 12.6 - Direction of steepest ascent and descent Consider...Ch. 12.6 - Direction of steepest ascent and descent Consider...Ch. 12.6 - Direction of steepest ascent and descent Consider...Ch. 12.6 - Direction of steepest ascent and descent Consider...Ch. 12.6 - Interpreting directional derivatives A function f...Ch. 12.6 - Interpreting directional derivatives A function f...Ch. 12.6 - Interpreting directional derivatives A function f...Ch. 12.6 - Interpreting directional derivatives A function f...Ch. 12.6 - Interpreting directional derivatives A function f...Ch. 12.6 - Interpreting directional derivatives A function f...Ch. 12.6 - Prob. 39ECh. 12.6 - Prob. 40ECh. 12.6 - Prob. 41ECh. 12.6 - Prob. 42ECh. 12.6 - Level curves Consider the paraboloid f(x, y) = 16 ...Ch. 12.6 - Level curves Consider the paraboloid f(x, y) = 16 ...Ch. 12.6 - Level curves Consider the paraboloid f(x, y) = 16 ...Ch. 12.6 - Level curves Consider the paraboloid f(x, y) = 16 ...Ch. 12.6 - Level curves Consider the upper half of the...Ch. 12.6 - Level curves Consider the upper half of the...Ch. 12.6 - Level curves Consider the upper half of the...Ch. 12.6 - Prob. 50ECh. 12.6 - Path of steepest descent Consider each of the...Ch. 12.6 - Path of steepest descent Consider each of the...Ch. 12.6 - Path of steepest descent Consider each of the...Ch. 12.6 - Path of steepest descent Consider each of the...Ch. 12.6 - Gradients in three dimensions Consider the...Ch. 12.6 - Gradients in three dimensions Consider the...Ch. 12.6 - Gradients in three dimensions Consider the...Ch. 12.6 - Gradients in three dimensions Consider the...Ch. 12.6 - Gradients in three dimensions Consider the...Ch. 12.6 - Gradients in three dimensions Consider the...Ch. 12.6 - Gradients in three dimensions Consider the...Ch. 12.6 - Gradients in three dimensions Consider the...Ch. 12.6 - Explain why or why not Determine whether the...Ch. 12.6 - Gradient of a composite function Consider the...Ch. 12.6 - Directions of zero change Find the directions in...Ch. 12.6 - Prob. 66ECh. 12.6 - Directions of zero change Find the directions in...Ch. 12.6 - Directions of zero change Find the directions in...Ch. 12.6 - Steepest ascent on a plane Suppose a long sloping...Ch. 12.6 - Gradient of a distance function Let (a, b) be a...Ch. 12.6 - Looking aheadtangent planes Consider the following...Ch. 12.6 - Prob. 72ECh. 12.6 - Looking aheadtangent planes Consider the following...Ch. 12.6 - Prob. 74ECh. 12.6 - Prob. 75ECh. 12.6 - Prob. 76ECh. 12.6 - Prob. 77ECh. 12.6 - Prob. 78ECh. 12.6 - Prob. 79ECh. 12.6 - Prob. 80ECh. 12.6 - Rules for gradients Use the definition of the...Ch. 12.6 - Prob. 82ECh. 12.6 - Prob. 83ECh. 12.6 - Prob. 84ECh. 12.6 - Prob. 85ECh. 12.6 - Prob. 86ECh. 12.6 - Prob. 87ECh. 12.7 - Suppose n is a vector normal to the tangent plane...Ch. 12.7 - Write the explicit function z = xy2 + x2y 10 in...Ch. 12.7 - Write an equation for the plane tangent to the...Ch. 12.7 - Prob. 4ECh. 12.7 - Explain how to approximate a function f at a point...Ch. 12.7 - Explain how to approximate the change in a...Ch. 12.7 - Write the approximate change formula for a...Ch. 12.7 - Write the differential dw for the function w =...Ch. 12.7 - Tangent planes for F(x,y,z) = 0 Find an equation...Ch. 12.7 - Tangent planes for F(x,y,z) = 0 Find an equation...Ch. 12.7 - Tangent planes for F(x,y,z) = 0 Find an equation...Ch. 12.7 - Tangent planes for F(x,y,z) = 0 Find an equation...Ch. 12.7 - Tangent planes for F(x,y,z) = 0 Find an equation...Ch. 12.7 - Tangent planes for F(x, y, z) = 0 Find an equation...Ch. 12.7 - Tangent planes for F(x, y, z) = 0 Find an equation...Ch. 12.7 - Tangent planes for F(x, y, z) = 0 Find an equation...Ch. 12.7 - Tangent planes for z = f (x, y) Find an equation...Ch. 12.7 - Tangent planes for z = f (x, y) Find an equation...Ch. 12.7 - Tangent planes for z = f (x, y) Find an equation...Ch. 12.7 - Tangent planes for z = f (x, y) Find an equation...Ch. 12.7 - Tangent planes for z = f (x, y) Find an equation...Ch. 12.7 - Prob. 22ECh. 12.7 - Tangent planes for z = f (x, y) Find an equation...Ch. 12.7 - Tangent planes for z = f (x, y) Find an equation...Ch. 12.7 - Linear approximation a.Find the linear...Ch. 12.7 - Linear approximation a.Find the linear...Ch. 12.7 - Linear approximation a.Find the linear...Ch. 12.7 - Linear approximation a.Find the linear...Ch. 12.7 - Linear approximation a.Find the linear...Ch. 12.7 - Prob. 30ECh. 12.7 - Approximate function change Use differentials to...Ch. 12.7 - Approximate function change Use differentials to...Ch. 12.7 - Approximate function change Use differentials to...Ch. 12.7 - Approximate function change Use differentials to...Ch. 12.7 - Changes in torus surface area The surface area of...Ch. 12.7 - Changes in cone volume The volume of a right...Ch. 12.7 - Area of an ellipse The area of an ellipse with...Ch. 12.7 - Volume of a paraboloid The volume of a segment of...Ch. 12.7 - Differentials with more than two variables Write...Ch. 12.7 - Differentials with more than two variables Write...Ch. 12.7 - Differentials with more than two variables Write...Ch. 12.7 - Differentials with more than two variables Write...Ch. 12.7 - Law of Cosines The side lengths of any triangle...Ch. 12.7 - Explain why or why not Determine whether the...Ch. 12.7 - Tangent planes Find an equation of the plane...Ch. 12.7 - Tangent planes Find an equation of the plane...Ch. 12.7 - Tangent planes Find an equation of the plane...Ch. 12.7 - Tangent planes Find an equation of the plane...Ch. 12.7 - Horizontal tangent planes Find the points at which...Ch. 12.7 - Horizontal tangent planes Find the points at which...Ch. 12.7 - Horizontal tangent planes Find the points at which...Ch. 12.7 - Horizontal tangent planes Find the points at which...Ch. 12.7 - Prob. 54ECh. 12.7 - Surface area of a cone A cone with height h and...Ch. 12.7 - Line tangent to an intersection curve Consider the...Ch. 12.7 - Water-level changes A conical tank with radius...Ch. 12.7 - Prob. 59ECh. 12.7 - Floating-point operations In general, real numbers...Ch. 12.7 - Probability of at least one encounter Suppose that...Ch. 12.7 - Prob. 62ECh. 12.7 - Prob. 63ECh. 12.7 - Prob. 64ECh. 12.7 - Logarithmic differentials Let f be a...Ch. 12.8 - Describe the appearance of a smooth surface with a...Ch. 12.8 - Describe the usual appearance of a smooth surface...Ch. 12.8 - What are the conditions for a critical point of a...Ch. 12.8 - If fx (a, b) = fy (a, b) = 0, does it follow the f...Ch. 12.8 - Consider the function z = f(x, y). What is the...Ch. 12.8 - Prob. 6ECh. 12.8 - What is an absolute minimum value of a function f...Ch. 12.8 - What is the procedure for locating absolute...Ch. 12.8 - Critical points Find all critical points of the...Ch. 12.8 - Critical points Find all critical points of the...Ch. 12.8 - Critical points Find all critical points of the...Ch. 12.8 - Critical points Find all critical points of the...Ch. 12.8 - Critical points Find all critical points of the...Ch. 12.8 - Critical points Find all critical points of the...Ch. 12.8 - Critical points Find all critical points of the...Ch. 12.8 - Prob. 16ECh. 12.8 - Critical points Find all critical points of the...Ch. 12.8 - Prob. 18ECh. 12.8 - Prob. 19ECh. 12.8 - Prob. 20ECh. 12.8 - Prob. 21ECh. 12.8 - Prob. 22ECh. 12.8 - Prob. 23ECh. 12.8 - Prob. 24ECh. 12.8 - Analyzing critical points Find the critical points...Ch. 12.8 - Analyzing critical points Find the critical points...Ch. 12.8 - Prob. 27ECh. 12.8 - Prob. 28ECh. 12.8 - Analyzing critical points Find the critical points...Ch. 12.8 - Analyzing critical points Find the critical points...Ch. 12.8 - Prob. 31ECh. 12.8 - Prob. 32ECh. 12.8 - Analyzing critical points Find the critical points...Ch. 12.8 - Prob. 34ECh. 12.8 - Shipping regulations A shipping company handles...Ch. 12.8 - Cardboard boxes A lidless box is to be made using...Ch. 12.8 - Cardboard boxes A lidless cardboard box is to be...Ch. 12.8 - Optimal box Find the dimensions of the largest...Ch. 12.8 - Prob. 39ECh. 12.8 - Inconclusive tests Show that the Second Derivative...Ch. 12.8 - Prob. 41ECh. 12.8 - Inconclusive tests Show that the Second Derivative...Ch. 12.8 - Absolute maxima and minima Find the absolute...Ch. 12.8 - Absolute maxima and minima Find the absolute...Ch. 12.8 - Absolute maxima and minima Find the absolute...Ch. 12.8 - Absolute maxima and minima Find the absolute...Ch. 12.8 - Absolute maxima and minima Find the absolute...Ch. 12.8 - Absolute maxima and minima Find the absolute...Ch. 12.8 - Absolute maxima and minima Find the absolute...Ch. 12.8 - Absolute maxima and minima Find the absolute...Ch. 12.8 - Prob. 51ECh. 12.8 - Absolute maxima and minima Find the absolute...Ch. 12.8 - Absolute extrema on open and / or unbounded...Ch. 12.8 - Absolute extrema on open and / or unbounded...Ch. 12.8 - Absolute extrema on open and / or unbounded...Ch. 12.8 - Absolute extrema on open and / or unbounded...Ch. 12.8 - Prob. 57ECh. 12.8 - Prob. 58ECh. 12.8 - Prob. 59ECh. 12.8 - Absolute extrema on open and / or unbounded...Ch. 12.8 - Explain why or why not Determine whether the...Ch. 12.8 - Prob. 62ECh. 12.8 - Extreme points from contour plots Based on the...Ch. 12.8 - Optimal box Find the dimensions of the rectangular...Ch. 12.8 - Lease distance What point on the plane x y + z =...Ch. 12.8 - Maximum/minimum of linear functions Let R be a...Ch. 12.8 - Magic triples Let x, y, and z be nonnegative...Ch. 12.8 - Powers and roots Assume that x + y + z = 1 with x ...Ch. 12.8 - Prob. 69ECh. 12.8 - Least squares approximation In its many guises,...Ch. 12.8 - Prob. 71ECh. 12.8 - Prob. 72ECh. 12.8 - Prob. 73ECh. 12.8 - Second Derivative Test Suppose the conditions of...Ch. 12.8 - Maximum area triangle Among all triangles with a...Ch. 12.8 - Ellipsoid inside a tetrahedron (1946 Putnam Exam)...Ch. 12.8 - Slicing plane Find an equation of the plane...Ch. 12.8 - Two mountains without a saddle Show that the...Ch. 12.8 - Solitary critical points A function of one...Ch. 12.9 - Explain why, at a point that maximizes or...Ch. 12.9 - Prob. 2ECh. 12.9 - Prob. 3ECh. 12.9 - Prob. 4ECh. 12.9 - Lagrange multipliers in two variables Use Lagrange...Ch. 12.9 - Lagrange multipliers in two variables Use Lagrange...Ch. 12.9 - Lagrange multipliers in two variables Use Lagrange...Ch. 12.9 - Lagrange multipliers in two variables Use Lagrange...Ch. 12.9 - Lagrange multipliers in two variables Use Lagrange...Ch. 12.9 - Lagrange multipliers in two variables Use Lagrange...Ch. 12.9 - Prob. 11ECh. 12.9 - Lagrange multipliers in two variables Use Lagrange...Ch. 12.9 - Prob. 13ECh. 12.9 - Lagrange multipliers in two variables Use Lagrange...Ch. 12.9 - Lagrange multipliers in three variables Use...Ch. 12.9 - Lagrange multipliers in three variables Use...Ch. 12.9 - Lagrange multipliers in three variables Use...Ch. 12.9 - Lagrange multipliers in three variables Use...Ch. 12.9 - Prob. 19ECh. 12.9 - Lagrange multipliers in three variables Use...Ch. 12.9 - Lagrange multipliers in three variables Use...Ch. 12.9 - Prob. 22ECh. 12.9 - Prob. 23ECh. 12.9 - Lagrange multipliers in three variables Use...Ch. 12.9 - Applications of Lagrange multipliers Use Lagrange...Ch. 12.9 - Prob. 26ECh. 12.9 - Prob. 27ECh. 12.9 - Prob. 28ECh. 12.9 - Prob. 29ECh. 12.9 - Prob. 30ECh. 12.9 - Prob. 31ECh. 12.9 - Prob. 32ECh. 12.9 - Prob. 33ECh. 12.9 - Applications of Lagrange multipliers Use Lagrange...Ch. 12.9 - Maximizing utility functions Find the values of l...Ch. 12.9 - Maximizing utility functions Find the values of l...Ch. 12.9 - Maximizing utility functions Find the values of l...Ch. 12.9 - Maximizing utility functions Find the values of l...Ch. 12.9 - Explain why or why not Determine whether the...Ch. 12.9 - Prob. 40ECh. 12.9 - Prob. 41ECh. 12.9 - Prob. 42ECh. 12.9 - Prob. 43ECh. 12.9 - Prob. 44ECh. 12.9 - Prob. 45ECh. 12.9 - Prob. 46ECh. 12.9 - Prob. 47ECh. 12.9 - Prob. 48ECh. 12.9 - Prob. 49ECh. 12.9 - Graphical Lagrange multipliers The following...Ch. 12.9 - Graphical Lagrange multipliers The following...Ch. 12.9 - Extreme points on flattened spheres The equation...Ch. 12.9 - Production functions Economists model the output...Ch. 12.9 - Production functions Economists model the output...Ch. 12.9 - Production functions Economists model the output...Ch. 12.9 - Temperature of an elliptical plate The temperature...Ch. 12.9 - Maximizing a sum 57.Find the maximum value of x1 +...Ch. 12.9 - Prob. 58ECh. 12.9 - Prob. 59ECh. 12.9 - Geometric and arithmetic means Given positive...Ch. 12.9 - Problems with two constraints Given a...Ch. 12.9 - Prob. 62ECh. 12.9 - Two-constraint problems Use the result of Exercise...Ch. 12.9 - Prob. 64ECh. 12.9 - Two-constraint problems Use the result of Exercise...Ch. 12 - Prob. 1RECh. 12 - Prob. 2RECh. 12 - Equations of planes Consider the plane passing...Ch. 12 - Intersecting planes Find an equation of the line...Ch. 12 - Intersecting planes Find an equation of the line...Ch. 12 - Prob. 6RECh. 12 - Equations of planes Find an equation of the...Ch. 12 - Identifying surfaces Consider the surfaces defined...Ch. 12 - Identifying surfaces Consider the surfaces defined...Ch. 12 - Identifying surfaces Consider the surfaces defined...Ch. 12 - Identifying surfaces Consider the surfaces defined...Ch. 12 - Identifying surfaces Consider the surfaces defined...Ch. 12 - Identifying surfaces Consider the surfaces defined...Ch. 12 - Identifying surfaces Consider the surfaces defined...Ch. 12 - Identifying surfaces Consider the surfaces defined...Ch. 12 - Identifying surfaces Consider the surfaces defined...Ch. 12 - Identifying surfaces Consider the surfaces defined...Ch. 12 - Identifying surfaces Consider the surfaces defined...Ch. 12 - Identifying surfaces Consider the surfaces defined...Ch. 12 - Identifying surfaces Consider the surfaces defined...Ch. 12 - Prob. 21RECh. 12 - Identifying surfaces Consider the surfaces defined...Ch. 12 - Prob. 23RECh. 12 - Prob. 24RECh. 12 - Prob. 25RECh. 12 - Prob. 26RECh. 12 - Prob. 27RECh. 12 - Level curves Make a sketch of several level curves...Ch. 12 - Prob. 29RECh. 12 - Matching level curves with surfaces Match level...Ch. 12 - Prob. 31RECh. 12 - Prob. 32RECh. 12 - Prob. 33RECh. 12 - Prob. 34RECh. 12 - Prob. 35RECh. 12 - Prob. 36RECh. 12 - Prob. 37RECh. 12 - Prob. 38RECh. 12 - Prob. 39RECh. 12 - Prob. 40RECh. 12 - Prob. 41RECh. 12 - Prob. 42RECh. 12 - Prob. 43RECh. 12 - Prob. 44RECh. 12 - Prob. 45RECh. 12 - Prob. 46RECh. 12 - Prob. 47RECh. 12 - Laplaces equation Verify that the following...Ch. 12 - Prob. 49RECh. 12 - Prob. 50RECh. 12 - Prob. 51RECh. 12 - Chain Rule Use the Chain Rule to evaluate the...Ch. 12 - Prob. 53RECh. 12 - Implicit differentiation Find dy/dx for the...Ch. 12 - Implicit differentiation Find dy/dx for the...Ch. 12 - Walking on a surface Consider the following...Ch. 12 - Walking on a surface Consider the following...Ch. 12 - Constant volume cones Suppose the radius of a...Ch. 12 - Directional derivatives Consider the function f(x,...Ch. 12 - Computing gradients Compute the gradient of the...Ch. 12 - Computing gradients Compute the gradient of the...Ch. 12 - Computing gradients Compute the gradient of the...Ch. 12 - Computing gradients Compute the gradient of the...Ch. 12 - Prob. 64RECh. 12 - Prob. 65RECh. 12 - Direction of steepest ascent and descent a.Find...Ch. 12 - Prob. 67RECh. 12 - Level curves Let f(x, y) = 8 2x2 y2. For the...Ch. 12 - Level curves Let f(x, y) = 8 2x2 y2. For the...Ch. 12 - Prob. 70RECh. 12 - Prob. 71RECh. 12 - Tangent planes Find an equation of the plane...Ch. 12 - Tangent planes Find an equation of the plane...Ch. 12 - Prob. 74RECh. 12 - Prob. 75RECh. 12 - Prob. 76RECh. 12 - Prob. 77RECh. 12 - Linear approximation a.Find the linear...Ch. 12 - Linear approximation a.Find the linear...Ch. 12 - Changes in a function Estimate the change in the...Ch. 12 - Volume of a cylinder The volume of a cylinder with...Ch. 12 - Volume of an ellipsoid The volume of an ellipsoid...Ch. 12 - Water-level changes A hemispherical tank with a...Ch. 12 - Prob. 84RECh. 12 - Analyzing critical points Identify the critical...Ch. 12 - Analyzing critical points Identify the critical...Ch. 12 - Analyzing critical points Identify the critical...Ch. 12 - Absolute maxima and minima Find the absolute...Ch. 12 - Absolute maxima and minima Find the absolute...Ch. 12 - Prob. 90RECh. 12 - Absolute maxima and minima Find the absolute...Ch. 12 - Prob. 92RECh. 12 - Lagrange multipliers Use Lagrange multipliers to...Ch. 12 - Prob. 94RECh. 12 - Lagrange multipliers Use Lagrange multipliers to...Ch. 12 - Lagrange multipliers Use Lagrange multipliers to...Ch. 12 - Maximum perimeter rectangle Use Lagrange...Ch. 12 - Minimum surface area cylinder Use Lagrange...Ch. 12 - Minimum distance to a cone Find the point(s) on...Ch. 12 - Prob. 100RE

Additional Math Textbook Solutions

Find more solutions based on key concepts
CHECK POINT I You deposit $1000 in a saving account at a bank that has a rate of 4%. a. Find the amount, A, of ...

Thinking Mathematically (6th Edition)

Three cards are randomly selected, without replacement, from an ordinary deck of 52 playing cards. Compute the ...

A First Course in Probability (10th Edition)

In problems 7-18, match each graph to one of the following functions: A. y= x 2 +2 B. y=- x 2 +2 C. y=| x |+2 D...

Precalculus

In hypothesis testing, the common level of significance is =0.05. Some might argue for a level of significance ...

Basic Business Statistics, Student Value Edition

Find the point-slope form of the line passing through the given points. Use the first point as (x1, .y1). Plot ...

College Algebra with Modeling & Visualization (5th Edition)

Here is the region of integration of the integral Rewrite the integral as an equivalent iterated integral in ...

University Calculus: Early Transcendentals (4th Edition)

Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
PREALGEBRA
Algebra
ISBN:9781938168994
Author:OpenStax
Publisher:OpenStax
Text book image
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Text book image
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
College Algebra
Algebra
ISBN:9781337282291
Author:Ron Larson
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Area Between The Curve Problem No 1 - Applications Of Definite Integration - Diploma Maths II; Author: Ekeeda;https://www.youtube.com/watch?v=q3ZU0GnGaxA;License: Standard YouTube License, CC-BY