
(a)
Whether the equation
4 x − 3 y = 12 ℝ 3
(a)
Answer to Problem 1RE
The statement is false.
Explanation of Solution
Given:
The equation is
Calculation:
The graph of the given equation
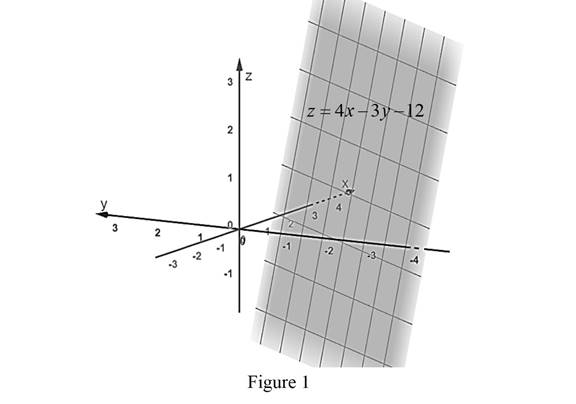
From Figure 1, it is observed that the given equation represents a plane in
So, the given statement the equation
Therefore, the statement is false.
(b)
Whether the equation
z 2 = 2 x 2 − 6 y 2
(b)
Answer to Problem 1RE
The statement is false.
Explanation of Solution
Given:
The equation is
Calculation:
The given equation is
If
Obtain the function in terms of x and y.
The functions are
Thus, z as a two function in terms of x and y.
Therefore, the statement is false.
(c)
Whether the function f satisfies the derivative
f x x y = f y y x
(c)
Answer to Problem 1RE
The statement is false.
Explanation of Solution
Let the function f has a continuous partial derivatives of all orders.
Then prove that
For example, assume
Obtain the value of
Take partial derivative of the function f with respect to x and obtain
Thus,
Take partial derivative of the equation (1) with respect to x and obtain
Hence,
Again, take partial derivative for the equation (2) with respect to y and obtain
Therefore,
Obtain the value of
Take partial derivative of the function f with respect to y and obtain
Thus,
Take partial derivative of the equation (1) with respect to y and obtain
Hence,
Again, take partial derivative for the equation (2) with respect to x and obtain
Therefore,
From above, it is concluded that
Thus,
Therefore, the statement is false.
(d)
Whether the gradient
∇ f ( a , b ) ( a , b , f ( a , b ) )
(d)
Answer to Problem 1RE
The statement is false.
Explanation of Solution
Given:
The surface is
Theorem used: The Gradient and Level Curves
“Given a function f differentiable at
Calculation:
The given surface is
Assume the critical point be
Then, the given function is differentiable at
Thus, the gradient of
By above theorem, it can be concluded that the line tangent to the level curve of f at
But it does not satisfy the given statement. Because, it is given that the the gradient
Since,
Therefore, the statement is false.
(e)
Whether the plane is always orthogonal to both the distinct intersecting planes.
(e)
Answer to Problem 1RE
The statement is true.
Explanation of Solution
Assume the equations of a plane.
The normal
Therefore, the statement is true.
Want to see more full solutions like this?
Chapter 12 Solutions
Student Solutions Manual, Single Variable for Calculus: Early Transcendentals
- Please answer JAVA OOP question below: An Employee has a name, employee ID, and department. An Employee object must be created with all its attributes. The UML diagram is provided below: - name: String - employeeId: String - department: String + Employee(name: String, employeeId: String, department: String) + setName(name: String): void + setEmployeeId(employeeId: String): void + setDepartment(department: String): void + getName(): String + getEmployeeId(): String + getDepartment(): String + toString(): String A faculty is an Employee with an additional field String field: rank Assuming the Employee class is fully implemented, define a Professor class in Java with the following: Instance variable(s) A Constructorarrow_forwardDevelop a C++ program that execute the operation as stated by TM for addition of two binary numbers (see attached image). Your code should receive two binary numbers and output the resulting sum (also in binary). Make sure your code mimics the TM operations (dealing with the binary numbers as a string of characters 1 and 0, and following the logic to increase the first number and decreasing the second one. Try your TM for the following examples: 1101 and 101, resulting 10010; and 1101 and 11, resulting 10000.arrow_forwardI need to define and discuss the uses of one monitoring or troubleshooting tool in Windows Server 2019. thank youarrow_forward
- I would likr toget help with the following concepts: - Windows Server features - Windows Server versus Windows 10 used as a client-server networkarrow_forwardI need to define and discuss the uses of one monitoring or troubleshooting tool in Windows Server 2019. thank youarrow_forwardWhy is planning for the retirement system and transition critical?arrow_forward
 C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr
C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole
Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole

