Chapter 11.10, Problem 65P

Consider a two-stage cascade refrigeration cycle with a flash chamber as shown in the figure with refrigerant-134a as the working fluid. The evaporator temperature is −10°C and the condenser pressure is 1600 kPa. The refrigerant leaves the condenser as a saturated liquid and is throttled to a flash chamber operating at 0.45 MPa. Part of the refrigerant evaporates during this flashing process, and this vapor is mixed with the refrigerant leaving the low-pressure compressor. The mixture is then compressed to the condenser pressure by the high-pressure compressor. The liquid in the flash chamber is throttled to the evaporator pressure and cools the refrigerated space as it vaporizes in the evaporator. The mass flow rate of the refrigerant through the low-pressure compressor is 0.11 kg/s. Assuming the refrigerant leaves the evaporator as a saturated vapor and the isentropic efficiency is 86 percent for both compressors, determine (a) the mass flow rate of the refrigerant through the high-pressure compressor, (b) the rate of refrigeration supplied by the system, and (c) the COP of this refrigerator. Also, determine (d) the rate of refrigeration and the COP if this refrigerator operated on a single-stage vapor-compression cycle between the same evaporating temperature and condenser pressure with the same compressor efficiency and the same flow rate as calculated in part a.

FIGURE P11–65

To determine

The mass flow rate of the refrigerant through the high-pressure compressor.

Answer to Problem 65P

The mass flow rate of the refrigerant through the high-pressure compressor is $\text{0}\text{.17074}\text{kg}/\text{s}$.

Explanation of Solution

Show the T-s diagram as in Figure (1).

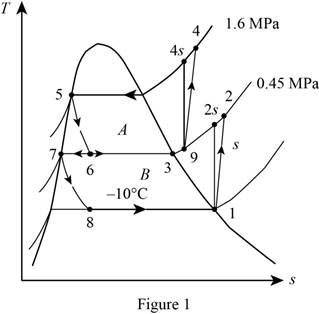
From Figure (1), write the specific enthalpy at state 6 is equal to state 5 due to throttling process.

$h_6\cong h_5$ (I)

Here, specific enthalpy at state 6 and 5 is $h_6\text{and}{h}_5$ respectively.

From Figure (1), write the specific enthalpy at state 8 is equal to state 7 due to throttling process.

$h_8\cong h_7$ (II)

Here, specific enthalpy at state 8 and 7 is $h_8\text{and}{h}_7$ respectively.

Express enthalpy at state 1.

$h_1=h_{g@-\text{10°C}}$ (III)

Here, enthalpy saturation vapor at temperature of $-10\text{°C}$ is $h_{g@-\text{10°C}}$.

Express entropy at state 1.

$s_1=s_{g@-\text{10°C}}$ (IV)

Here, entropy saturation vapor at temperature of $-10°\text{C}$ is $s_{g@-\text{10°C}}$.

Express the specific enthalpy at state 2.

${\eta }_C=\frac{h_{2s}-h_1}{h_2-h_1}$ (V)

Here, specific enthalpy at state 2s is $h_{2s}$, isentropic efficiency is ${\eta }_C$ and specific enthalpy at state 1 and 2 is $h_1\text{and}{h}_2$ respectively.

Express enthalpy at state 3.

$h_3=h_{g@\text{450}\text{kPa}}$ (VI)

Here, enthalpy saturation vapor at pressure of $\text{450}\text{kPa}$ is $h_{g@\text{450}\text{kPa}}$.

Express enthalpy at state 5.

$h_5=h_{f@1600\text{kPa}}$ (VII)

Here, enthalpy saturation liquid at pressure of $\text{1600}\text{kPa}$ is $h_{f@1600\text{kPa}}$.

Express enthalpy at state 7.

$h_7=h_{f@450\text{kPa}}$ (VIII)

Here, enthalpy saturation liquid at pressure of $\text{450}\text{kPa}$ is $h_{f@450\text{kPa}}$.

Express the quality at state 6.

$x_6=\frac{h_6-h_{f@450\text{kPa}}}{h_{g@450\text{kPa}}-h_{f@450\text{kPa}}}$ (IX)

Express the mass flow rate of the refrigerant.

$\dot{m}=\frac{{\dot{m}}_7}{1-x_6}$ (X)

Here, mass flow rate at state 7 is ${\dot{m}}_7$.

Conclusion:

Refer Table A-11, “saturated refrigerant-134a-temperature table”, and write enthalpy saturation vapor at temperature of $-10\text{°C}$.

$h_{g@-\text{10°C}}=244.55\text{kJ}/\text{kg}$

Substitute $244.55\text{kJ}/\text{kg}$ for $h_{g@-\text{10°C}}$ in Equation (III).

$h_1=244.55\text{kJ}/\text{kg}$

Refer Table A-11, “saturated refrigerant-134a-temperature table”, and write entropy saturation vapor at temperature of $-10\text{°C}$.

$s_{g@-\text{10°C}}=0.9382\text{kJ}/\text{kg}\cdot \text{K}$

Substitute $0.9382\text{kJ}/\text{kg}\cdot \text{K}$ for $s_{g@-\text{10°C}}$ in Equation (IV).

$s_1=0.9382\text{kJ}/\text{kg}\cdot \text{K}$

Perform the unit conversion of pressure at state 2 from $\text{kPa}\text{to}\text{MPa}$.

$\begin{array}{c}{P}_2=450\text{kPa}\\ =450\text{kPa}\left[\frac{\text{MPa}}{1000\text{kPa}}\right]\\ =0.45\text{MPa}\end{array}$

Refer Table A-13, “superheated refrigerant 134a”, and write the specific enthalpy at state 2s corresponding to pressure at state 2 of $0.45\text{MPa}$ and specific entropy at state 2 $\left(s_2=s_1\right)$ of $0.9382\text{kJ}/\text{kg}\cdot \text{K}$ using an interpolation method.

$h_{2s}=261.10\text{kJ}/\text{kg}$

Here, enthalpy at state 2s is $h_{2s}$.

Substitute $0.86$ for ${\eta }_C$, $261.10\text{kJ}/\text{kg}$ for $h_{2s}$ and $244.55\text{kJ}/\text{kg}$ for $h_1$ in Equation (V).

$\begin{array}{l}0.86=\frac{261.10\text{kJ}/\text{kg}-244.55\text{kJ}/\text{kg}}{h_2-244.55\text{kJ}/\text{kg}}\\ 0.86h_2-210.313\text{kJ}/\text{kg}=16.55\text{kJ}/\text{kg}\\ 0.86h_2=226.863\text{kJ}/\text{kg}\\ h_2=263.79\text{kJ}/\text{kg}\end{array}$

Refer Table A-12, “saturated refrigerant-134a-pressure table”, and write the enthalpy saturation vapor at pressure of $\text{450}\text{kPa}$.

$h_{g@\text{450}\text{kPa}}=257.58\text{kJ}/\text{kg}$

Substitute $257.58\text{kJ}/\text{kg}$ for $h_{g@\text{450}\text{kPa}}$ in Equation (VI).

$h_3=257.58\text{kJ}/\text{kg}$

Refer Table A-12, “saturated refrigerant-134a-pressure table”, and write the enthalpy saturation liquid at pressure of $\text{1600}\text{kPa}$.

$h_{f@160\text{0}\text{kPa}}=135.96\text{kJ}/\text{kg}$

Substitute $135.96\text{kJ}/\text{kg}$ for $h_{f@160\text{0}\text{kPa}}$ in Equation (VII).

$h_5=135.96\text{kJ}/\text{kg}$

Substitute $135.96\text{kJ}/\text{kg}$ for $h_5$ in Equation (I).

$h_6=135.96\text{kJ}/\text{kg}$

Refer Table A-12, “saturated refrigerant-134a-pressure table”, and write the enthalpy saturation liquid at pressure of $\text{450}\text{kPa}$.

$h_{f@45\text{0}\text{kPa}}=68.80\text{kJ}/\text{kg}$

Substitute $68.80\text{kJ}/\text{kg}$ for $h_{f@45\text{0}\text{kPa}}$ in Equation (VIII).

$h_7=68.80\text{kJ}/\text{kg}$

Substitute $68.80\text{kJ}/\text{kg}$ for $h_7$ in Equation (II).

$h_8=68.80\text{kJ}/\text{kg}$

Substitute $\text{135}\text{.96}\text{kJ}/\text{kg}$ for $h_6$, $68.80\text{kJ}/\text{kg}$ for $h_{f@450\text{kPa}}$ and $257.58\text{kJ}/\text{kg}$ for $h_{g@450\text{kPa}}$ in Equation (IX).

$\begin{array}{c}{x}_6=\frac{\text{135}\text{.96}\text{kJ}/\text{kg}-68.80\text{kJ}/\text{kg}}{257.58\text{kJ}/\text{kg}-68.80\text{kJ}/\text{kg}}\\ =\frac{67.16}{188.78}\\ =0.35576\end{array}$

Substitute $\text{0}\text{.11}\text{kg}/\text{s}$ for ${\dot{m}}_7$ and $0.35576$ for $x_6$ in Equation (X).

$\begin{array}{c}\dot{m}=\frac{\text{0}\text{.11}\text{kg}/\text{s}}{1-0.35576}\\ =0.17074\text{kg}/\text{s}\end{array}$

Hence, the mass flow rate of the refrigerant through the high-pressure compressor is $\text{0}\text{.17074}\text{kg}/\text{s}$.

To determine

The rate of refrigeration supplied by the system.

Answer to Problem 65P

The rate of refrigeration supplied by the system is $\text{19}\text{.33}\text{kW}$.

Explanation of Solution

Express the mass flow rate at state 3.

${\dot{m}}_3=\dot{m}-{\dot{m}}_7$ (XI)

Express the enthalpy at state 9.

$h_9=\frac{{\dot{m}}_7{h}_2+{\dot{m}}_3{h}_3}{\dot{m}}$ (XII)

Express the enthalpy at state 4.

${\eta }_C=\frac{h_{4s}-h_9}{h_4-h_9}$ (XIII)

Here, specific enthalpy at state 4s is $h_{4s}$.

Express the rate of heat removal from the refrigerated space.

${\dot{Q}}_L={\dot{m}}_7\left(h_1-h_8\right)$ (XIV)

Conclusion:

Substitute $\text{0}\text{.17074}\text{kg}/\text{s}$ for $\dot{m}$ and $\text{0}\text{.11}\text{kg}/\text{s}$ for ${\dot{m}}_7$ in Equation (XI)

$\begin{array}{c}{\dot{m}}_3=\text{0}\text{.17074}\text{kg}/\text{s}-\text{0}\text{.11}\text{kg}/\text{s}\\ =0.06074\text{kg}/\text{s}\end{array}$

Substitute $\text{0}\text{.17074}\text{kg}/\text{s}$ for $\dot{m}$, $\text{0}\text{.11}\text{kg}/\text{s}$ for ${\dot{m}}_7$, $0.06074\text{kg}/\text{s}$ for ${\dot{m}}_3$, $\text{263}\text{.79}\text{kJ}/\text{kg}$ for $h_2$ and $\text{257}\text{.58}\text{kJ}/\text{kg}$ for $h_3$ in Equation (XII)

$\begin{array}{c}{h}_9=\frac{\left(\text{0}\text{.11}\text{kg}/\text{s}\right)\left(\text{263}\text{.79}\text{kJ}/\text{kg}\right)+\left(0.06074\text{kg}/\text{s}\right)\left(\text{257}\text{.58}\text{kJ}/\text{kg}\right)}{\text{0}\text{.17074}\text{kg}/\text{s}}\\ =261.58\text{kJ}/\text{kg}\end{array}$

Refer Table A-13, “superheated refrigerant 134a”, and write the specific enthalpy at state 9 corresponding to pressure at state 9 of $0.45\text{MPa}$ and specific enthalpy at state 9 of $261.58\text{kJ}/\text{kg}$ using an interpolation method.

$s_9=0.9399\text{kJ}/\text{kg}\cdot \text{K}$

Here, entropy at state 9 is $s_9$.

Refer Table A-13, “superheated refrigerant 134a”, and write the specific enthalpy at state 4s corresponding to pressure at state 4 of $1.6\text{MPa}\left(1600\text{kPa}\right)$ and specific entropy at state 4 $\left(s_9=s_4\right)$ of $0.9399\text{kJ}/\text{kg}\cdot \text{K}$ using an interpolation method.

Write the formula of interpolation method of two variables.

$y_2=\frac{\left(x_2-x_1\right)\left(y_3-y_1\right)}{\left(x_3-x_1\right)}+y_1$ (XV)

Here, the variables denote by x and y is specific entropy at state 9 and specific enthalpy at state 4s respectively.

Show the specific enthalpy at state 4s corresponding to specific entropy as in Table (1).

Specific entropy at state 9 $s_9\left(\text{kJ}/\text{kg}\cdot \text{K}\right)$	Specific enthalpy at state 4s $h_{4s}\left(\text{kJ}/\text{kg}\right)$
0.9164 $\left(x_1\right)$	280.71 $\left(y_1\right)$
0.9399 $\left(x_2\right)$	$\left(y_2=?\right)$
0.9536 $\left(x_3\right)$	293.27 $\left(y_3\right)$

Substitute $\text{0}\text{.9164}\text{kJ}/\text{kg}\cdot \text{K}\text{,}0.9399\text{kJ}/\text{kg}\cdot \text{K}\text{and}\text{0}\text{.9536}\text{kJ}/\text{kg}\cdot \text{K}$ for $x_1,x_2\text{and}{x}_3$ respectively, $280.71\text{kJ}/\text{kg}$ for $y_1$ and $293.27\text{kJ}/\text{kg}$ for $y_3$ in Equation (XV).

$\begin{array}{c}{y}_2=\frac{\left[\left(0.9399-\text{0}\text{.9164}\right)\text{kJ}/\text{kg}\cdot \text{K}\right]\left[\left(293.27-280.71\right)\text{kJ}/\text{kg}\right]}{\left(\text{0}\text{.9536}-\text{0}\text{.9164}\right)\text{kJ}/\text{kg}\cdot \text{K}}+280.71\text{kJ}/\text{kg}\\ =288.64\text{kJ}/\text{kg}\\ =h_{4s}\end{array}$

Thus, the specific enthalpy at state 4s is,

$h_{4s}=288.64\text{kJ}/\text{kg}$

Substitute $0.86$ for ${\eta }_C$, $288.64\text{kJ}/\text{kg}$ for $h_{4s}$ and $261.58\text{kJ}/\text{kg}$ for $h_9$ in Equation (XIII).

$\begin{array}{l}0.86=\frac{288.64\text{kJ}/\text{kg}-261.58\text{kJ}/\text{kg}}{h_2-261.58\text{kJ}/\text{kg}}\\ h_4=293.05\text{kJ}/\text{kg}\end{array}$

Substitute $\text{0}\text{.11}\text{kg}/\text{s}$ for ${\dot{m}}_7$, $\text{244}\text{.55}\text{kJ}/\text{kg}\text{and}\text{68}\text{.80}\text{kJ}/\text{kg}$ for $h_1\text{and}{h}_8$ in Equation (XIV).

$\begin{array}{c}{\dot{Q}}_L=\text{0}\text{.11}\text{kg}/\text{s}\left(\text{244}\text{.55}\text{kJ}/\text{kg}-\text{68}\text{.80}\text{kJ}/\text{kg}\right)\\ =19.33\text{kJ}/\text{s}\left[\frac{\text{kW}}{\text{kJ}/\text{s}}\right]\\ =19.33\text{kW}\end{array}$

Hence, the rate of refrigeration supplied by the system is $\text{19}\text{.33}\text{kW}$.

To determine

The COP of the refrigerator.

Answer to Problem 65P

The COP of the refrigerator is $\text{2}\text{.58}$.

Explanation of Solution

Express the power input.

${\dot{W}}_{\text{in}}={\dot{m}}_7\left(h_2-h_1\right)+\dot{m}\left(h_4-h_9\right)$ (XVI)

Express the coefficient of performance.

$\text{COP}=\frac{{\dot{Q}}_L}{{\dot{W}}_{\text{in}}}$ (XVII)

Conclusion:

Substitute $\text{263}\text{.79}\text{kJ}/\text{kg,}\text{244}\text{.55}\text{kJ}/\text{kg,}\text{293}\text{.05}\text{kJ}/\text{kg,}\text{and}\text{261}\text{.58}\text{kJ}/\text{kg}$ for $h_2,h_1,h_4$ and $h_7$ respectively, $\text{0}\text{.11}\text{kg}/\text{s}$ for ${\dot{m}}_7$ and $\text{0}\text{.17074}\text{kg}/\text{s}$ for $\dot{m}$ in Equation (XVI).

$\begin{array}{c}{\dot{W}}_{\text{in}}=\text{0}\text{.11}\text{kg}/\text{s}\left[\left(\text{263}\text{.79}-\text{244}\text{.55}\right)\text{kJ}/\text{kg}\right]+\text{0}\text{.17074}\text{kg}/\text{s}\left[\left(\text{293}\text{.05}-\text{261}\text{.58}\right)\text{kJ}/\text{kg}\right]\\ =7.490\text{kJ}/\text{s}\left[\frac{\text{kW}}{\text{kJ}/\text{s}}\right]\\ =7.490\text{kW}\end{array}$

Substitute $\text{19}\text{.33}\text{kW}$ for ${\dot{Q}}_L$ and $\text{7}\text{.490}\text{kW}$ for ${\dot{W}}_{\text{in}}$ IN Equation (XVII).

$\begin{array}{c}\text{COP}=\frac{\text{19}\text{.33}\text{kW}}{\text{7}\text{.490}\text{kW}}\\ =2.58\end{array}$

Hence, the coefficient of performance of the refrigerator is $\text{2}\text{.58}$.

To determine

The rate of refrigeration and the COP of the refrigerator.

Answer to Problem 65P

The rate of refrigeration is $\text{18}\text{.54}\text{kW}$ and the COP of the refrigerator is $2.15$.

Explanation of Solution

Show the T-s diagram as in Figure (1).

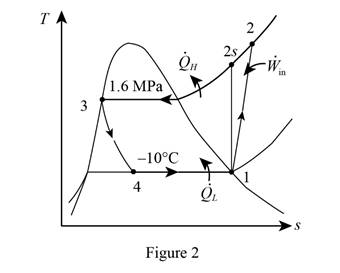
From Figure (1), write the specific enthalpy at state 4 is equal to state 3 due to throttling process.

$h_4\cong h_3$ (XVIII)

Here, specific enthalpy at state 4 and 3 is $h_4\text{and}{h}_3$ respectively.

Express the enthalpy at state 2.

${\eta }_C=\frac{h_{2s}-h_1}{h_2-h_1}$ (XIX)

Here, specific enthalpy at state 2s is $h_{2s}$.

Express enthalpy at state 3.

$h_3=h_{g@1600\text{kPa}}$ (XX)

Here, enthalpy saturation vapor at pressure of $\text{1600}\text{kPa}$ is $h_{g@1600\text{kPa}}$.

Express the rate of refrigeration.

${\dot{Q}}_L=\dot{m}\left(h_1-h_4\right)$ (XXI)

Express the rate of work input.

${\dot{W}}_{\text{in}}=\dot{m}\left(h_2-h_1\right)$ (XXII)

Express the coefficient of performance.

$\text{COP}=\frac{{\dot{Q}}_L}{{\dot{W}}_{\text{in}}}$ (XXIII)

Conclusion:

Refer Table A-13, “superheated refrigerant 134a”, and write the specific enthalpy at state 2s corresponding to pressure at state 2 of $1.6\text{MPa}\left(1600\text{kPa}\right)$ and specific entropy at state 2 $\left(s_2=s_1\right)$ of $0.9378\text{kJ}/\text{kg}\cdot \text{K}$ using an interpolation method.

Show the specific enthalpy at state 2s corresponding to specific entropy as in Table (2).

Specific entropy at state 2 $s_2\left(\text{kJ}/\text{kg}\cdot \text{K}\right)$	Specific enthalpy at state 2s $h_{2s}\left(\text{kJ}/\text{kg}\right)$
0.9164 $\left(x_1\right)$	280.71 $\left(y_1\right)$
0.9378 $\left(x_2\right)$	$\left(y_2=?\right)$
0.9536 $\left(x_3\right)$	293.27 $\left(y_3\right)$

Use excels and tabulates the values from Table (2) in Equation (XV) to get,

$\begin{array}{c}{y}_2=287.94\text{kJ}/\text{kg}\\ =h_{2s}\end{array}$

Thus, the specific enthalpy at state 2s is,

$h_{2s}=287.94\text{kJ}/\text{kg}$

Substitute $0.86$ for ${\eta }_C$, $287.94\text{kJ}/\text{kg}$ for $h_{2s}$ and $244.55\text{kJ}/\text{kg}$ for $h_1$ in Equation (XIX).

$\begin{array}{l}0.86=\frac{287.94\text{kJ}/\text{kg}-244.55\text{kJ}/\text{kg}}{h_2-244.55\text{kJ}/\text{kg}}\\ h_2=295\text{kJ}/\text{kg}\end{array}$

Refer Table A-12, “saturated refrigerant-134a-pressure table”, and write the enthalpy saturation liquid at pressure of $\text{1600}\text{kPa}$.

$h_{f@160\text{0}\text{kPa}}=135.96\text{kJ}/\text{kg}$

Substitute $135.96\text{kJ}/\text{kg}$ for $h_{f@160\text{0}\text{kPa}}$ in Equation (XX).

$h_3=135.96\text{kJ}/\text{kg}$

Substitute $135.96\text{kJ}/\text{kg}$ for $h_3$ in Equation (XVIII).

$h_4=135.96\text{kJ}/\text{kg}$

Substitute $\text{0}\text{.17074}\text{kg}/\text{s}$ for $\dot{m}$, $135.96\text{kJ}/\text{kg}$ for $h_4$ and $244.55\text{kJ}/\text{kg}$ for $h_1$ in Equation (XXI).

$\begin{array}{c}{\dot{Q}}_L=\text{0}\text{.17074}\text{kg}/\text{s}\left(244.55\text{kJ}/\text{kg}-135.96\text{kJ}/\text{kg}\right)\\ =18.54\text{kJ}/\text{s}\left[\frac{\text{kW}}{\text{kJ}/\text{s}}\right]\\ =18.54\text{kW}\end{array}$

Hence, the rate of refrigeration is $\text{18}\text{.54}\text{kW}$

Substitute $\text{0}\text{.17074}\text{kg}/\text{s}$ for $\dot{m}$, $295\text{kJ}/\text{kg}$ for $h_2$ and $244.55\text{kJ}/\text{kg}$ for $h_1$ in Equation (XXII).

$\begin{array}{c}{\dot{W}}_{\text{in}}=\text{0}\text{.17074}\text{kg}/\text{s}\left(295\text{kJ}/\text{kg}-244.55\text{kJ}/\text{kg}\right)\\ =8.614\text{kJ}/\text{s}\left[\frac{\text{kW}}{\text{kJ}/\text{s}}\right]\\ =8.614\text{kW}\end{array}$

Substitute $18.54\text{kW}$ for ${\dot{Q}}_L$ and $8.614\text{kW}$ for ${\dot{W}}_{\text{in}}$ in Equation (XXIII).

$\begin{array}{c}\text{COP}=\frac{18.54\text{kW}}{8.614\text{kW}}\\ =2.15\end{array}$

Hence, the coefficient of performance of the refrigerator is $2.15$.