
An air conditioner operates on the vapor-compression refrigeration cycle with refrigerant-134a as the refrigerant. The air conditioner is used to keep a space at 21°C while rejecting the waste heat to the ambient air at 37°C. The refrigerant enters the compressor at 180 kPa superheated by 2.7°C at a rate of 0.06 kg/s and leaves the compressor at 1200 kPa and 60°C. R-134a is subcooled by 6.3°C at the exit of the condenser. Determine (a) the rate of cooling provided to the space, in Btu/h, and the COP, (b) the isentropic efficiency and the exergy efficiency of the compressor, (c) the exergy destruction in each component of the cycle and the total exergy destruction in the cycle, and (d) the minimum power input and the second-law efficiency of the cycle.
(a)
The rate of cooling provided to the space.
The coefficient of performance of the air conditioner.
Answer to Problem 118RP
The rate of cooling provided to the space is
The coefficient of performance of the air conditioner is
Explanation of Solution
Show the T-s diagram as in Figure (1).
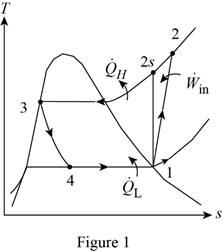
Express the refrigeration load.
Here, specific enthalpy at state 1 and 4 is
Express the rate of work input.
Express the coefficient of performance of the air conditioner.
Conclusion:
Perform the unit conversion of pressure at state 1 from
Refer to Table A-13, obtain the saturation temperature at a pressure of 0.18 MPa as
Calculate the temperature at state 1.
Substitute
Refer Table A-13, “superheated refrigerant-134a”, and write the properties corresponding to pressure and inlet temperature of
Here, specific enthalpy and entropy is
Write the formula of interpolation method of two variables.
Here, the variables denote by x and y is specific entropy at state 2 and specific enthalpy at state 2s respectively.
Show the specific enthalpy at state 2s corresponding to specific entropy by referring the table A-13 at pressure of 1.2 MPa and specific entropy of
|
Specific entropy at state 2 |
Specific enthalpy at state 2s |
| 0.9268 | 278.28 |
| 0.9484 | |
| 0.9615 | 289.66 |
Substitute the Table (1) values in Equation (IV) to get 285.34 kJ/kg.
Thus, the specific enthalpy at state 2s is,
Refer Table A-13, “superheated refrigerant-134a”, and write the properties corresponding to exit state of pressure and temperature of
Here, specific enthalpy and entropy at exit state are
Refer to Table A-13, obtain the saturation temperature at a pressure of 1.2 MPa as
Refer Table A-13, “superheated refrigerant-134a”, and write the properties corresponding to state 3 of pressure and temperature of
Here, specific enthalpy and entropy at state 3 are
Refer Table A-13, “superheated refrigerant-134a”, and write the properties corresponding to state 4 of pressure and specific enthalpy of
Substitute 0.06 kg/s for
Thus, the rate of cooling provided to the space is
Substitute 0.06 kg/s for
Substitute 2.670 kW for
Thus, the coefficient of performance of the air conditioner is
(b)
The isentropic efficiency of the compressor.
The exergy efficiency of the compressor.
Answer to Problem 118RP
The isentropic efficiency of the compressor is
The exergy efficiency of the compressor is
Explanation of Solution
Express the isentropic efficiency of the compressor.
Here, specific enthalpy at state 2s is
Calculate the reversible power for the compressor.
Here, ambient air temperature is
Calculate the exergy efficiency for the compressor.
Conclusion:
Substitute 285.34 kJ/kg for
Thus, the isentropic efficiency of the compressor is
Substitute 0.06 kg/s for
Substitute 2.428 kW for
Thus, the exergy efficiency of the compressor is
(c)
The exergy destruction in each component of the cycle.
The total exergy destruction in the cycle.
Answer to Problem 118RP
The exergy destruction in each component of the cycle are
The total exergy destruction in the cycle is
Explanation of Solution
Compressor
Express the entropy generation for cycle 1-2.
Express the exergy destruction for the cycle 1-2.
Condenser
Express the entropy generation for cycle 2-3.
Here, the rate of heat rejected is
Calculate the value of
Substitute
Express the exergy destruction for the cycle 2-3.
Expansion valve
Express the entropy generation for cycle 3-4.
Express the exergy destruction for the cycle 3-4.
Evaporator
Express the entropy generation for cycle 4-1.
Here, temperature at refrigeration load is
Express the exergy destruction for the cycle 4-1.
Calculate the total exergy destruction.
Conclusion:
Substitute 0.06 kg/s for
Substitute
Substitute 0.06 kg/s for
Substitute
Substitute 0.06 kg/s for
Substitute
Substitute 0.06 kg/s for
Substitute
Thus, the exergy destruction in each component of the cycle are
Substitute 0.2426 kW for
Thus, the total exergy destruction in the cycle is
(d)
The minimum power input of the cycle.
The second law efficiency of the cycle.
Answer to Problem 118RP
The minimum power input of the cycle is
The second law efficiency of the cycle is
Explanation of Solution
Express the exergy of the heat transferred from the low-temperature medium.
Here, minimum power input of the cycle is the exergy of the heat transferred from the low-temperature medium.
Calculate the second law efficiency of the cycle.
Calculate the total exergy destruction in the cycle.
Conclusion:
Substitute 8.213 kW for
Thus, the minimum power input to the cycle is
Substitute 0.4470 kW for
Thus, the second law efficiency of the cycle is
Want to see more full solutions like this?
Chapter 11 Solutions
THERMODYNAMICS (LL)-W/ACCESS >CUSTOM<
- Using the Bernoulli equation to find the general solution. If an initial condition is given, find the particular solution. y' + xy = xy¯¹, y(0) = 3arrow_forwardTest for exactness. If exact, solve. If not, use an integrating factor as given or obtained by inspection or by the theorems in the text. a. 2xydx+x²dy = 0 b. (x2+y2)dx-2xydy = 0 c. 6xydx+5(y + x2)dy = 0arrow_forwardNewton's law of cooling. A thermometer, reading 5°C, is brought into a room whose temperature is 22°C. One minute later the thermometer reading is 12°C. How long does it take until the reading is practically 22°C, say, 21.9°C?arrow_forward
- Solve a. y' + 2xy = ex-x² b. y' + y sin x = ecosx, y(0) = −1 y(0) = −2.5arrow_forward= MMB 241 Tutorial 3.pdf 2/6 90% + + 5. The boat is traveling along the circular path with a speed of v = (0.0625t²) m/s, where t is in seconds. Determine the magnitude of its acceleration when t = 10 s. 40 m v = 0.0625² 6. If the motorcycle has a deceleration of at = (0.001s) m/s² and its speed at position A is 25 m/s, determine the magnitude of its acceleration when it passes point B. .A 90° 300 m n B 2arrow_forward= MMB 241 Tutorial 3.pdf 4/6 67% + 9. The car is traveling along the road with a speed of v = (2 s) m/s, where s is in meters. Determine the magnitude of its acceleration when s = 10 m. v = (2s) m/s 50 m 10. The platform is rotating about the vertical axis such that at any instant its angular position is u = (4t 3/2) rad, where t is in seconds. A ball rolls outward along the radial groove so that its position is r = (0.1+³) m, where t is in seconds. Determine the magnitudes of the velocity and acceleration of the ball when t = 1.5s.arrow_forward
- The population of a certain country is known to increase at a rate proportional to the number of people presently living in the country. If after two years the population has doubled, and after three years the population is 20,000, estimate the number of people initially living in the country.arrow_forward= MMB 241 Tutorial 3.pdf 6/6 100% + | 日 13. The slotted link is pinned at O, and as a result of the constant angular velocity *= 3 rad/s it drives the peg P for a short distance along the spiral guide r = (0.40) m, where 0 is in radians. Determine the radial and transverse components of the velocity and acceleration of P at the instant = 1/3 rad. 0.5 m P r = 0.40 =3 rad/sarrow_forward= MMB 241 Tutorial 3.pdf 1/6 90% + DYNAMICS OF PARTICLES (MMB 241) Tutorial 3 Topic: Kinematics of Particles:- Path and Polar coordinate systems and general curvilinear QUESTIONS motion. 1. Determine the acceleration at s = 2 m if v = (2 s) m/s², where s is in meters. At s = 0, v = 1 m/s. 3 m 2. Determine the acceleration when t=1s if v = (4t2+2) m/s, where t is in seconds. v=(4²+2) m/s 6 marrow_forward
- 5.112 A mounting bracket for electronic components is formed from sheet metal with a uniform thickness. Locate the center of gravity of the bracket. 0.75 in. 3 in. ༧ Fig. P5.112 1.25 in. 0.75 in. y r = 0.625 in. 2.5 in. 1 in. 6 in. xarrow_forward4-105. Replace the force system acting on the beam by an equivalent resultant force and couple moment at point B. A 30 in. 4 in. 12 in. 16 in. B 30% 3 in. 10 in. 250 lb 260 lb 13 5 12 300 lbarrow_forwardSketch and Describe a hatch coaming and show how the hatch coamings are framed in to ships strucure?arrow_forward
 Refrigeration and Air Conditioning Technology (Mi...Mechanical EngineeringISBN:9781305578296Author:John Tomczyk, Eugene Silberstein, Bill Whitman, Bill JohnsonPublisher:Cengage Learning
Refrigeration and Air Conditioning Technology (Mi...Mechanical EngineeringISBN:9781305578296Author:John Tomczyk, Eugene Silberstein, Bill Whitman, Bill JohnsonPublisher:Cengage Learning
