Chemistry
4th Edition
ISBN: 9780078021527
Author: Julia Burdge
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 10.5, Problem 5CP
In the following diagram, each color represents a different gas molecule. Calculate the mole fraction of each gas.
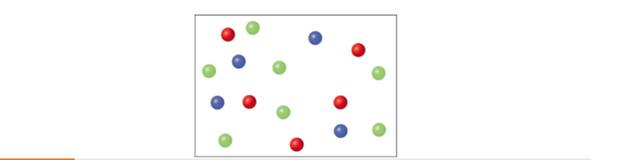a)
b)
c)
d)
e)
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 10 Solutions
Chemistry
Ch. 10.1 - Practice ProblemATTEMPT What pressure (in atm) is...Ch. 10.1 - Prob. 1PPBCh. 10.1 - Prob. 1PPCCh. 10.1 - Express a pressure of 1 .15 atm in units of bar....Ch. 10.1 - Prob. 2CPCh. 10.1 - Prob. 3CPCh. 10.1 - Prob. 4CPCh. 10.1 - Prob. 5CPCh. 10.2 - Prob. 1PPACh. 10.2 - Practice ProblemBUILD At what pressure would a...
Ch. 10.2 - Prob. 1PPCCh. 10.2 - 10.2.1 Given .
Ch. 10.2 - Prob. 2CPCh. 10.2 - 10.2.3 At what temperature will a gas sample...Ch. 10.2 - What volume of NH 3 will be produced when 180 mL...Ch. 10.2 - Prob. 5CPCh. 10.2 - Prob. 6CPCh. 10.3 - Practice ProblemATTEMPT A sample of gas originally...Ch. 10.3 - Practice ProblemBUILD At what temperature (in °C )...Ch. 10.3 - Prob. 1PPCCh. 10.3 - Prob. 1CPCh. 10.3 - Prob. 2CPCh. 10.3 - Prob. 3CPCh. 10.3 - Prob. 4CPCh. 10.4 - Practice ProblemATTEMPT What volume (in liters) of...Ch. 10.4 - Practice ProblemBUILD What volumes (in liters) of...Ch. 10.4 - Practice Problem CONCEPTUALIZE
A hypothetical...Ch. 10.4 - Prob. 1CPCh. 10.4 - Prob. 2CPCh. 10.5 - Practice Problem ATTEMPT
What would be the volume...Ch. 10.5 - Prob. 1PPBCh. 10.5 - Prob. 1PPCCh. 10.5 - Prob. 1CPCh. 10.5 - Prob. 2CPCh. 10.5 - Prob. 3CPCh. 10.5 - 10.5.4 What mass of acetylene is produced by the...Ch. 10.5 - In the following diagram, each color represents a...Ch. 10.5 - Prob. 6CPCh. 10.6 - Practice ProblemATTEMPT What is the volume of 5.12...Ch. 10.6 - Practice ProblemBUILD At what temperature ( in °C...Ch. 10.6 - Practice Problem CONCEPTUALIZE
The diagram shown...Ch. 10.6 - Prob. 1CPCh. 10.6 - Prob. 2CPCh. 10.7 - Practice Problem ATTEMPT
Calculate the density of...Ch. 10.7 - Prob. 1PPBCh. 10.7 - Prob. 1PPCCh. 10.7 - Prob. 1CPCh. 10.7 - Prob. 2CPCh. 10.8 - Practice Problem ATTEMPT Determine the molar mass...Ch. 10.8 - Practice Problem BUILD
A sample of the volatile...Ch. 10.8 - Practice ProblemCONCEPTUALIZE These models...Ch. 10.9 - Practice Problem ATTEMPT
What volume (in liters)...Ch. 10.9 - Practice Problem BUILD What mass (in grams) of Na...Ch. 10.9 - Prob. 1PPCCh. 10.10 - Practice Problem ATTEMPT Using all the same...Ch. 10.10 - Practice ProblemBUILD By how much would the...Ch. 10.10 - Prob. 1PPCCh. 10.11 - Prob. 1PPACh. 10.11 - Prob. 1PPBCh. 10.11 - Prob. 1PPCCh. 10.12 - Practice Problem ATTEMPT Determine the partial...Ch. 10.12 - Practice Problem BUILD
Determine the number of...Ch. 10.12 - Prob. 1PPCCh. 10.13 - Prob. 1PPACh. 10.13 - Practice ProblemBUILD Determine the partial...Ch. 10.13 - Prob. 1PPCCh. 10.14 - Practice Problem ATTEMPT
Calculate the mass of ...Ch. 10.14 - Practice ProblemBUILD Determine the volume of gas...Ch. 10.14 - Practice ProblemCONCEPTUALIZE The first diagram...Ch. 10.15 - Prob. 1PPACh. 10.15 - Practice ProblemBUILD What chamber pressure would...Ch. 10.15 - Practice ProblemCONCEPTUALIZE The diagram on the...Ch. 10.16 - Prob. 1PPACh. 10.16 - Practice ProblemBUILD Determine the molar mass and...Ch. 10.16 - Practice ProblemCONCEPTUALIZE The diagram on the...Ch. 10.17 - Practice ProblemATTEMPT Using data from Table...Ch. 10.17 - Practice ProblemBUILD Calculate the pressure...Ch. 10.17 - Practice ProblemCONCEPTUALIZE What properties of...Ch. 10 - Determine the mole fraction of helium in a gaseous...Ch. 10 - Prob. 2KSPCh. 10 - Determine the mole fraction of water in a solution...Ch. 10 - Prob. 4KSPCh. 10 - Prob. 1QPCh. 10 - Prob. 2QPCh. 10 - Prob. 3QPCh. 10 - Prob. 4QPCh. 10 - Prob. 5QPCh. 10 - Prob. 6QPCh. 10 - Prob. 7QPCh. 10 - Prob. 8QPCh. 10 - Prob. 9QPCh. 10 - Prob. 10QPCh. 10 - Prob. 11QPCh. 10 - Prob. 12QPCh. 10 - Prob. 13QPCh. 10 - Prob. 14QPCh. 10 - Calculate the height of a column of methanol (C H...Ch. 10 - Prob. 16QPCh. 10 - What pressure (in atm) is exerted by a column of...Ch. 10 - What pressure (in atm) is exerted by a column of...Ch. 10 - Prob. 19QPCh. 10 - Prob. 20QPCh. 10 - Prob. 21QPCh. 10 - Prob. 22QPCh. 10 - Prob. 23QPCh. 10 - A sample of air occupies 3.8 L when the pressure...Ch. 10 - Prob. 25QPCh. 10 - 10.26 Under constant-pressure conditions a sample...Ch. 10 - 10.27 Ammonia bums in oxygen gas to form nitric...Ch. 10 - Molecular chlorine and molecular fluorine combine...Ch. 10 - A gaseous sample of a substance is cooled at...Ch. 10 - Consider the following gaseous sample in a...Ch. 10 - Prob. 31QPCh. 10 - Prob. 32QPCh. 10 - Prob. 33QPCh. 10 - Prob. 34QPCh. 10 - 10.35 Given that 6.9 moles of carbon monoxide gas...Ch. 10 - What volume will 9.8 moles of sulfur hexafluoride...Ch. 10 - Prob. 37QPCh. 10 - Prob. 38QPCh. 10 - Prob. 39QPCh. 10 - An ideal gas originally at 0.85 atm and 66°C was...Ch. 10 - Calculate the volume (in liters) of 124.3 g of CO...Ch. 10 - Prob. 42QPCh. 10 - Prob. 43QPCh. 10 - Prob. 44QPCh. 10 - At 741 torr and 44°C, 7.10 g of a gas occupies a...Ch. 10 - Prob. 46QPCh. 10 - Assuming that air contains 78 percent N 2 , 21...Ch. 10 - 10.48 A 2.10-L vessel contains 4.65 g of a gas at...Ch. 10 - Calculate the density of hydrogen bromide ( HBr )...Ch. 10 - A certain anesthetic contains 64.9 percent C, 13.5...Ch. 10 - A compound has the empirical formula SF 4 . At...Ch. 10 - Prob. 52QPCh. 10 - Prob. 53QPCh. 10 - Prob. 54QPCh. 10 - Methane, the principal component of natural gas,...Ch. 10 - Prob. 56QPCh. 10 - In alcohol fermentation, yeast converts glucose to...Ch. 10 - A compound of P and F was analyzed as follows:...Ch. 10 - 10.59 A quantity of 0.225 g of a metal M (molar...Ch. 10 - Prob. 60QPCh. 10 - Prob. 61QPCh. 10 - Prob. 62QPCh. 10 - Ethanol ( C 2 H 5 OH ) burns in air: C 2 H 5 OH( l...Ch. 10 - Prob. 64QPCh. 10 - Prob. 65QPCh. 10 - Prob. 66QPCh. 10 - A 2.5-L flask at 15°C contains a mixture of N 2 ,...Ch. 10 - Dry air near sea level has the following...Ch. 10 - Prob. 69QPCh. 10 - Prob. 70QPCh. 10 - 10.71 A sample of zinc metal reacts completely...Ch. 10 - Prob. 72QPCh. 10 - Prob. 73QPCh. 10 - Prob. 74QPCh. 10 - 10.75 The volume of the box on the right is twice...Ch. 10 - Prob. 76QPCh. 10 - Prob. 77QPCh. 10 - Prob. 78QPCh. 10 - Prob. 79QPCh. 10 - Prob. 80QPCh. 10 - Prob. 81QPCh. 10 - Compare the root-mean-square speeds of O 2 and U F...Ch. 10 - Prob. 83QPCh. 10 - Prob. 84QPCh. 10 - 10.85 At a certain temperature the speeds of six...Ch. 10 - Prob. 86QPCh. 10 - Prob. 87QPCh. 10 - Prob. 88QPCh. 10 - Prob. 89QPCh. 10 - Cite two pieces of evidence to show that gases do...Ch. 10 - Figure 10.25(a) shows that at o°C , with the...Ch. 10 - 10.92 Write the van der Waals equation for a real...Ch. 10 - Prob. 93QPCh. 10 - Prob. 94QPCh. 10 - Prob. 95QPCh. 10 - 10.96 Discuss the following phenomena in terms of...Ch. 10 - Prob. 97APCh. 10 - Prob. 98APCh. 10 - Prob. 99APCh. 10 - Prob. 100APCh. 10 - Prob. 101APCh. 10 - Prob. 102APCh. 10 - On heating, potassium chlorate ( KClO 3 )...Ch. 10 - Prob. 104APCh. 10 - Prob. 105APCh. 10 - Prob. 106APCh. 10 - Prob. 107APCh. 10 - Prob. 108APCh. 10 - Prob. 109APCh. 10 - Prob. 110APCh. 10 - A mixture of Na 2 CO 3 and MgCO 3 of mass 7.63 g...Ch. 10 - Prob. 112APCh. 10 - Prob. 113APCh. 10 - Prob. 114APCh. 10 - Prob. 115APCh. 10 - Prob. 116APCh. 10 - Prob. 117APCh. 10 - Prob. 118APCh. 10 - Prob. 119APCh. 10 - Prob. 120APCh. 10 - Prob. 121APCh. 10 - Prob. 122APCh. 10 - Prob. 123APCh. 10 - Prob. 124APCh. 10 - Prob. 125APCh. 10 - Prob. 126APCh. 10 - Prob. 127APCh. 10 - Prob. 128APCh. 10 - Prob. 129APCh. 10 - Prob. 130APCh. 10 - Prob. 131APCh. 10 - Prob. 132APCh. 10 - Prob. 133APCh. 10 - Prob. 134APCh. 10 - Prob. 135APCh. 10 - Prob. 136APCh. 10 - Prob. 137APCh. 10 - Prob. 138APCh. 10 - Prob. 139APCh. 10 - Given that the van der Waals constant b is the...Ch. 10 - Prob. 141APCh. 10 - Prob. 142APCh. 10 - Prob. 143APCh. 10 - Prob. 144APCh. 10 - Prob. 145APCh. 10 - Prob. 146APCh. 10 - Prob. 147APCh. 10 - Prob. 148APCh. 10 - A 5.00-mol sample of NH 3 gas is kept in a 1.92-L...Ch. 10 - In the metallurgical process of refining nickel,...Ch. 10 - Some commercial drain cleaners contain a mixture...Ch. 10 - Prob. 152APCh. 10 - Prob. 153APCh. 10 - Prob. 154APCh. 10 - Prob. 155APCh. 10 - 10. 156 Air entering the lungs ends up in tiny...Ch. 10 - Prob. 157APCh. 10 - Prob. 158APCh. 10 - Prob. 159APCh. 10 - Prob. 160APCh. 10 - The percent by mass of bicarbonate ( HCO 3 ) in a...Ch. 10 - Prob. 162APCh. 10 - Prob. 163APCh. 10 - Prob. 164APCh. 10 - Prob. 165APCh. 10 - Prob. 166APCh. 10 - Prob. 167APCh. 10 - Venus's atmosphere is composed of 96.5 percent CO...Ch. 10 - Acidic oxides such as carbon dioxide react with...Ch. 10 - Prob. 170APCh. 10 - 10.171 In a constant-pressure calorimetry...Ch. 10 - Prob. 2SEPPCh. 10 - Prob. 3SEPPCh. 10 - Prob. 4SEPP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, chemistry and related others by exploring similar questions and additional content below.Similar questions
- 2. The volume of a gas sample is 235 mL at a temperature of 25 ℃. At what temperature would that same gas sample have a volume of 310. mL, if the pressure of the gas sample is held constant? −47.0 ℃ 69.4 ℃ 33.1 ℃ 120.℃arrow_forwardPlot the data given in Table 5.3 for oxygen at 0C to obtain an accurate molar mass for O2. To do this, calculate a value of the molar mass at each of the given pressures from the ideal gas law (we will call this the apparent molar mass at this pressure). On a graph show the apparent molar mass versus the pressure and extrapolate to find the molar mass at zero pressure. Because the ideal gas law is most accurate at low pressures, this extrapolation will give an accurate value for the molar mass. What is the accurate molar mass?arrow_forwardMany nitrate salts can be decomposed by heating. For example, blue, anhydrous copper(II) nitrate produces the gases nitrogen dioxide and oxygen when heated. In the laboratory, you find that a sample of this salt produced a 0.195-g mixture of gaseous NO2 and O2 with a total pressure of 725 mm Hg at 35 C in a 125-mL flask (and black, solid CuO was left as a residue). What is the average molar mass of the gas mixture? What are the mole fractions of NO2 and O2 in the mixture? What amount of each gas b in the mixture? Do these amounts reflect the relative amounts of NO2 and O2 expected based on the balanced equation? Is it possible that the fact that some NO2 molecules combine to give N2O4 plays a role? Heating copper(II) nitrate produces nitrogen dioxide and oxygen gas and leaves a residue of copper(ll) oxide.arrow_forward
- Pressures of gases in mixtures are referred to as partial pressures and are additive. 1.00 L of He gas at 0.75 atm is mixed with 2.00 L of Ne gas at 1.5 atm at a temperature of 25.0 C to make a total volume of 3.00 L of a mixture. Assuming no temperature change and that He and Ne can be approximated as ideal gases, what are a the total resulting pressure, b the partial pressures of each component, and c the mole fractions of each gas in the mix?arrow_forwardYou have a 550.-mL tank of gas with a pressure of 1.56 atm at 24 C. You thought the gas was pure carbon monoxide gas, CO, but you later found it was contaminated by small quantities of gaseous CO2 and O2. Analysis shows that the tank pressure is 1.34 atm (at 24 C) if the CO2 is removed. Another experiment shows that 0.0870 g of O2 can be removed chemically. What are the masses of CO and CO2 in the tank, and what is the partial pressure of each of the three gases at 25 C?arrow_forwardYou have a gas, one of the three known phosphorus-fluorine compounds (PF3, PF3, and P2F4). To find out which, you have decided to measure its molar mass. (a) First, yon determine that the density of the gas is 5.60 g/L at a pressure of 0.971 atm and a temperature of 18.2 C. Calculate the molar mass and identify the compound. (b) To check the results from part (a), you decide to measure the molar mass based on the relative rales of effusion of the unknown gas and CO2. You find that CO2 effuses at a rate of 0.050 mol/min, whereas the unknown phosphorus fluoride effuses at a rate of 0.028 mol/min. Calculate the molar mass of the unknown gas based on these results.arrow_forward
- A halothane-oxygen mixture (C2HBrCIF3 + O2) can be used as an anesthetic. A tank containing such a mixture has the following partial pressures: P (halothane) = 170 mm Hg and P (O2) = 570 mm Hg. (a) What is the ratio of the number of moles of halothane to the number of moles of O2? (b) If the tank contains 160 g of O2, what mass of C2HBrCIF3 is present?arrow_forwardA 1.000-g sample of an unknown gas at 0C gives the following data: P(atm) V (L) 0.2500 3.1908 0.5000 1.5928 0.7500 1.0601 1.0000 0.7930 Use these data to calculate the value of the molar mass at each of the given pressures from the ideal gas law (we will call this the apparent molar mass at this pressure). Plot the apparent molar masses against pressure and extrapolate to find the molar mass at zero pressure. Because the ideal gas law is most accurate at low pressures, this extrapolation will give an accurate value for the molar mass. What is the accurate molar mass?arrow_forwardConsider these four gas samples, all at the same temperature. The larger boxes have twice the volume of the smaller boxes. Rank the gas samples with respect to: (a) pressure, (b) density, (c) average kinetic energy, and (d) average molecular speed. (Green spheres are He; violet spheres are Ne.)arrow_forward
- Silane, SiH4, is the silicon analogue of methane, CH4. It is prepared industrially according to the following equations: Si(s)+3HC1(g)HSiCl3(l)+H2(g)4HSiCl3(l)SiH4(g)+3SiCl4(l) a. If 156 mL HSiCl3 (d = 1.34 g/mL) is isolated when 15.0 L HC1 at 10.0 atm and 35C is used, what is the percent yield of HSiCl3? b. When 156 mL HSiCl3 is heated, what volume of SiH4 at 10.0 atm and 35C will be obtained if the percent yield of the reaction is 93.1%?arrow_forward5-114 Carbon dioxide gas, saturated with water vapor, can be produced by the addition of aqueous acid to calcium carbonate based on the following balanced net ionic equation: (a) How many moles of wet CO (g), collected at 60.°C and 774 torr total pressure, are produced by the complete reaction of 10.0 g of CaCO3 with excess acid? (b) What volume does this wet CO2 occupy? (c) What volume would the CO2 occupy at 774 torr if a desiccant (a chemical drying agent) were added to remove the water? The vapor pressure of water at 60.°C is 149.4 mm Hg.arrow_forwardThe density of air 20 km above Earths surface is 92 g/m3. The pressure of the atmosphere is 42 mm Hg, and the temperature is 63 C. (a) What is the average molar mass of the atmosphere at this altitude? (b) If the atmosphere at this altitude consists of only O2 and N2, what is the mole fraction of each gas?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Introductory Chemistry: A FoundationChemistryISBN:9781337399425Author:Steven S. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning
Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning
Introductory Chemistry: A Foundation
Chemistry
ISBN:9781337399425
Author:Steven S. Zumdahl, Donald J. DeCoste
Publisher:Cengage Learning
Chemistry for Engineering Students
Chemistry
ISBN:9781337398909
Author:Lawrence S. Brown, Tom Holme
Publisher:Cengage Learning
Chemistry: An Atoms First Approach
Chemistry
ISBN:9781305079243
Author:Steven S. Zumdahl, Susan A. Zumdahl
Publisher:Cengage Learning
Chemistry & Chemical Reactivity
Chemistry
ISBN:9781337399074
Author:John C. Kotz, Paul M. Treichel, John Townsend, David Treichel
Publisher:Cengage Learning
Chemistry & Chemical Reactivity
Chemistry
ISBN:9781133949640
Author:John C. Kotz, Paul M. Treichel, John Townsend, David Treichel
Publisher:Cengage Learning
Chemistry: The Molecular Science
Chemistry
ISBN:9781285199047
Author:John W. Moore, Conrad L. Stanitski
Publisher:Cengage Learning
Step by Step Stoichiometry Practice Problems | How to Pass ChemistryMole Conversions Made Easy: How to Convert Between Grams and Moles; Author: Ketzbook;https://www.youtube.com/watch?v=b2raanVWU6c;License: Standard YouTube License, CC-BY