Thomas' Calculus and Linear Algebra and Its Applications Package for the Georgia Institute of Technology, 1/e
5th Edition
ISBN: 9781323132098
Author: Thomas, Lay
Publisher: PEARSON C
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 10.3, Problem 7E
Consider the mouse in the following maze from Section 10.1, Exercise 19.
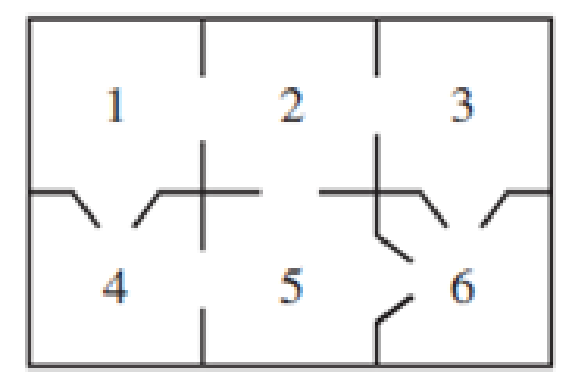
Find the communication classes for the Markov chain that models the mouse's travels through this maze. Is this Markov chain reducible or irreducible?
In Exercises 19 and 20. suppose a mouse wanders through the given maze, some of whose doors are “one-way”: they are just large enough for the mouse to squeeze through in only one direction. The mouse still must move into a different room at each time step if possible. When faced with accessible openings into two or more rooms, the mouse chooses them with equal probability.
19. The mouse is placed in room 1 of the maze shown below.
- a. Construct a transition matrix and an initial probability
vector for the mouse’s travels. - b. What arc the probabilities that the mouse will be in each of the rooms after 4 moves?
Expert Solution & Answer
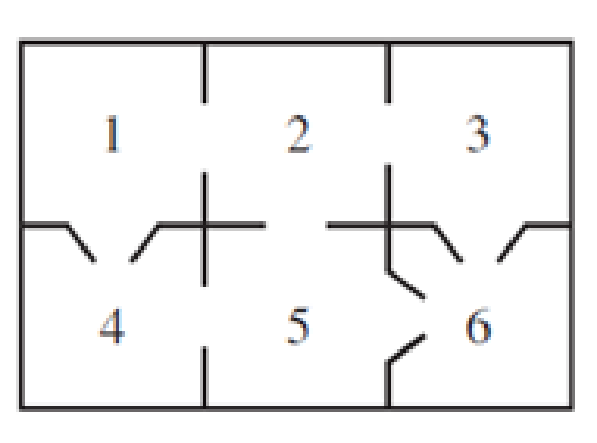
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Each item is inspected and is declared to either pass or fail. The machine can work in automatic or manual mode. If it outputs two failed items in a row in automatic mode, it is switched to manual. Once it produces two passing items in a row in manual mode, it is switched back to automatic. Sup- pose that failure rate is a in automatic and b in manual. You modeled the system as a Markov chain with a diagram given below, where states represent the mode and the status of the previously man- ufactured item, so for example, state “manual-1 success” represents that the machine is in manual mode and the previous item passed.
A state vectorX for a three-state Markov chain is such that the system is as likely to
be in state 3 as in state 2 and is three times as likely to be in state 1 as in 3. Find the
state vector X.
ZD In Smalltown, 90% of all sunny days are followed by
sunny days, and 80% of all cloudy days are followed by
cloudy days. Use this information to model Smalltown's
weather as a Markov chain.
Chapter 10 Solutions
Thomas' Calculus and Linear Algebra and Its Applications Package for the Georgia Institute of Technology, 1/e
Ch. 10.1 - Fill in the missing entries in the stochastic...Ch. 10.1 - Prob. 2PPCh. 10.1 - In Exercises 1 and 2, determine whether P is a...Ch. 10.1 - In Exercises 1 and 2, determine whether P is a...Ch. 10.1 - Prob. 3ECh. 10.1 - Prob. 4ECh. 10.1 - In Exercises 5 and 6, the transition matrix P for...Ch. 10.1 - Prob. 6ECh. 10.1 - In Exercises 7 and 8, the transition matrix P for...Ch. 10.1 - In Exercises 7 and 8, the transition matrix P for...
Ch. 10.1 - Consider a pair of Ehrenfest urns labeled A and B....Ch. 10.1 - Consider a pair of Ehrenfest urns labeled A and B....Ch. 10.1 - Consider an unbiased random walk on the set...Ch. 10.1 - Consider a biased random walk on the set {1,2,3,4}...Ch. 10.1 - In Exercises 13 and 14, find the transition matrix...Ch. 10.1 - In Exercises 13 and 14, find the transition matrix...Ch. 10.1 - In Exercises 15 and 16, find the transition matrix...Ch. 10.1 - In Exercises 15 and 16, find the transition matrix...Ch. 10.1 - The mouse is placed in room 2 of the maze shown...Ch. 10.1 - The mouse is placed in room 3 of the maze shown...Ch. 10.1 - Prob. 19ECh. 10.1 - In Exercises 19 and 20, suppose a mouse wanders...Ch. 10.1 - Prob. 21ECh. 10.1 - In Exercises 21 and 22, mark each statement True...Ch. 10.1 - The weather in Charlotte, North Carolina, can be...Ch. 10.1 - Suppose that whether it rains in Charlotte...Ch. 10.1 - Prob. 25ECh. 10.1 - Consider a set of five webpages hyperlinked by the...Ch. 10.1 - Consider a model for signal transmission in which...Ch. 10.1 - Consider a model for signal transmission in which...Ch. 10.1 - Prob. 29ECh. 10.1 - Another model for diffusion is called the...Ch. 10.1 - To win a game in tennis, one player must score...Ch. 10.1 - Volleyball uses two different scoring systems in...Ch. 10.1 - Prob. 33ECh. 10.2 - Consider the Markov chain on {1, 2, 3} with...Ch. 10.2 - In Exercises 1 and 2, consider a Markov chain on...Ch. 10.2 - Prob. 2ECh. 10.2 - In Exercises 3 and 4, consider a Markov chain on...Ch. 10.2 - Prob. 4ECh. 10.2 - Prob. 5ECh. 10.2 - In Exercises 5 and 6, find the matrix to which Pn...Ch. 10.2 - In Exercises 7 and 8, determine whether the given...Ch. 10.2 - Prob. 8ECh. 10.2 - Consider a pair of Ehrenfest urns with a total of...Ch. 10.2 - Consider a pair of Ehrenfest urns with a total of...Ch. 10.2 - Consider an unbiased random walk with reflecting...Ch. 10.2 - Consider a biased random walk with reflecting...Ch. 10.2 - Prob. 13ECh. 10.2 - In Exercises 13 and 14, consider a simple random...Ch. 10.2 - In Exercises 15 and 16, consider a simple random...Ch. 10.2 - In Exercises 15 and 16, consider a simple random...Ch. 10.2 - Prob. 17ECh. 10.2 - Prob. 18ECh. 10.2 - Prob. 19ECh. 10.2 - Consider the mouse in the following maze, which...Ch. 10.2 - In Exercises 21 and 22, mark each statement True...Ch. 10.2 - In Exercises 21 and 22, mark each statement True...Ch. 10.2 - Prob. 23ECh. 10.2 - Suppose that the weather in Charlotte is modeled...Ch. 10.2 - In Exercises 25 and 26, consider a set of webpages...Ch. 10.2 - In Exercises 25 and 26, consider a set of webpages...Ch. 10.2 - Prob. 27ECh. 10.2 - Consider beginning with an individual of known...Ch. 10.2 - Prob. 29ECh. 10.2 - Consider the Bernoulli-Laplace diffusion model...Ch. 10.2 - Prob. 31ECh. 10.2 - Prob. 32ECh. 10.2 - Prob. 33ECh. 10.2 - Let 0 p, q 1, and define P = [p1q1pq] a. Show...Ch. 10.2 - Let 0 p, q 1, and define P = [pq1pqq1pqp1pqpq]...Ch. 10.2 - Let A be an m m stochastic matrix, let x be in m...Ch. 10.2 - Prob. 37ECh. 10.2 - Consider a simple random walk on a finite...Ch. 10.2 - Prob. 39ECh. 10.3 - Consider the Markov chain on {1, 2, 3, 4} with...Ch. 10.3 - Prob. 1ECh. 10.3 - In Exercises 16, consider a Markov chain with...Ch. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Consider the mouse in the following maze from...Ch. 10.3 - Prob. 8ECh. 10.3 - Prob. 9ECh. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Consider an unbiased random walk with absorbing...Ch. 10.3 - In Exercises 13 and 14, consider a simple random...Ch. 10.3 - Prob. 14ECh. 10.3 - In Exercises 15 and 16, consider a simple random...Ch. 10.3 - In Exercises 15 and 16, consider a simple random...Ch. 10.3 - Consider the mouse in the following maze from...Ch. 10.3 - Consider the mouse in the following maze from...Ch. 10.3 - Prob. 19ECh. 10.3 - In Exercises 19 and 20, consider the mouse in the...Ch. 10.3 - Prob. 21ECh. 10.3 - Prob. 22ECh. 10.3 - Suppose that the weather in Charlotte is modeled...Ch. 10.3 - Prob. 24ECh. 10.3 - The following set of webpages hyperlinked by the...Ch. 10.3 - The following set of webpages hyperlinked by the...Ch. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Prob. 29ECh. 10.3 - Prob. 30ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 32ECh. 10.3 - Prob. 33ECh. 10.3 - In Exercises 33 and 34, consider the Markov chain...Ch. 10.3 - Prob. 35ECh. 10.3 - Prob. 36ECh. 10.4 - Consider the Markov chain on {1, 2, 3, 4} with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 7-10, consider a simple random walk...Ch. 10.4 - In Exercises 7-10, consider a simple random walk...Ch. 10.4 - In Exercises 7-10, consider a simple random walk...Ch. 10.4 - In Exercises 7-10: consider a simple random walk...Ch. 10.4 - Reorder the states in the Markov chain in Exercise...Ch. 10.4 - Reorder the states in the Markov chain in Exercise...Ch. 10.4 - Reorder the states in the Markov chain in Exercise...Ch. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Find the transition matrix for the Markov chain in...Ch. 10.4 - Find the transition matrix for the Markov chain in...Ch. 10.4 - Consider the mouse in the following maze from...Ch. 10.4 - Consider the mouse in the following maze from...Ch. 10.4 - In Exercises 21-22, mark each statement True or...Ch. 10.4 - In Exercises 21-22, mark each statement True or...Ch. 10.4 - Confirm Theorem 5 for the Markov chain in Exercise...Ch. 10.4 - Prob. 24ECh. 10.4 - Consider the Markov chain on {1, 2, 3} with...Ch. 10.4 - Follow the plan of Exercise 25 to confirm Theorem...Ch. 10.4 - Prob. 27ECh. 10.4 - Prob. 28ECh. 10.4 - Prob. 29ECh. 10.5 - Prob. 1PPCh. 10.5 - Consider a Markov chain on {1, 2, 3, 4} with...Ch. 10.5 - Prob. 1ECh. 10.5 - Prob. 2ECh. 10.5 - In Exercises 13, find the fundamental matrix of...Ch. 10.5 - Prob. 4ECh. 10.5 - Prob. 5ECh. 10.5 - Prob. 6ECh. 10.5 - Prob. 7ECh. 10.5 - Prob. 8ECh. 10.5 - Prob. 9ECh. 10.5 - Prob. 10ECh. 10.5 - Prob. 11ECh. 10.5 - Prob. 12ECh. 10.5 - Consider a simple random walk on the following...Ch. 10.5 - Consider a simple random walk on the following...Ch. 10.5 - Prob. 15ECh. 10.5 - Prob. 16ECh. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - Consider the mouse in the following maze from...Ch. 10.5 - In Exercises 21 and 22, mark each statement True...Ch. 10.5 - Prob. 22ECh. 10.5 - Suppose that the weather in Charlotte is modeled...Ch. 10.5 - Suppose that the weather in Charlotte is modeled...Ch. 10.5 - Consider a set of webpages hyperlinked by the...Ch. 10.5 - Consider a set of webpages hyperlinked by the...Ch. 10.5 - Exercises 27-30 concern the Markov chain model for...Ch. 10.5 - Exercises 27-30 concern the Markov chain model for...Ch. 10.5 - Exercises 27-30 concern the Markov chain model for...Ch. 10.5 - Exercises 27-30 concern the Markov chain model for...Ch. 10.5 - Exercises 31-36 concern the two Markov chain...Ch. 10.5 - Exercises 31-36 concern the two Markov chain...Ch. 10.5 - Exercises 31-36 concern the two Markov chain...Ch. 10.5 - Prob. 34ECh. 10.5 - Prob. 35ECh. 10.5 - Prob. 36ECh. 10.5 - Consider a Markov chain on {1, 2, 3, 4, 5, 6} with...Ch. 10.5 - Consider a Markov chain on {1,2,3,4,5,6} with...Ch. 10.5 - Prob. 39ECh. 10.6 - Let A be the matrix just before Example 1. Explain...Ch. 10.6 - Prob. 2PPCh. 10.6 - Prob. 1ECh. 10.6 - Prob. 2ECh. 10.6 - Prob. 3ECh. 10.6 - Prob. 4ECh. 10.6 - Prob. 5ECh. 10.6 - Prob. 6ECh. 10.6 - Major League batting statistics for the 2006...Ch. 10.6 - Prob. 8ECh. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - Prob. 11ECh. 10.6 - Prob. 12ECh. 10.6 - Prob. 14ECh. 10.6 - Prob. 15ECh. 10.6 - Prob. 16ECh. 10.6 - Prob. 17ECh. 10.6 - In the previous exercise, let p be the probability...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Explain how you can determine the steady state matrix X of an absorbing Markov chain by inspection.arrow_forward2. A rat runs through the maze shown below. At each step it leaves the room it is in by choosing at random one of the doors out of the room. 1 2 3 4 10 5 6 What are the communicating classes for this Markov chain? Are they periodic? Justify your answer.arrow_forwardIf A is a Markov matrix, why doesn't I+ A+ A2 + · · · add up to (I -A)-1?arrow_forward
- A Markov chain model for a species has four states: State 0 (Lower Risk), State 1 (Vulnerable), State 2 (Threatened), and State 3 (Extinct). For t 2 0, you are given that: 01 zit = 0.03 12 t= 0.05 23 Hit = 0.06 This species is currently in state 0. Calculate the probability this species will be in state 2 ten years later. Assume that reentry is not possible. (Note: This question is similar to #46.2 but with constant forces of mortality) Possīble Answers A 0.02 0.03 0.04 D 0.05 E 0.06arrow_forwardConsider the Markov chain X given by the diagram 0 10 1 12 2 FO 2 a) Write down the (1-step) transition matrix of the Markov chain. b) Calculate (manually) the n-step transition matrices of X (remember from linear algebra that matrix powers are best computed by diagonalizing the matrix first and realizing that the power has only to be applied to the diagonal part).arrow_forwardCan someone please help me with this question. I am having so much trouble.arrow_forward
- Please do Exercise 2 part A and B and please show step and explain. Topic of this question is Markov Chainsarrow_forwardA Markov system with two states satisfies the following rule. If you are in state 1 then of the time you change to state 2. If you are in state 2 then of the time you remain in state 2. At time t = 0, there are 100 people in state 1 and no people in the other state. state 1 Write the transition matrix for this system using the state vector v = state 2 T = Write the state vector for time t = 0. Vo Compute the state vectors for time t = 1 and t = 2. Vị = V2arrow_forwardRobots have been programmed to traverse the maze shown in the figure below and at each junction randomly choose which way to go. (a) Construct the transition matrix for the Markov chain that models this situation. 1 3 4 1 2 3 1 Ø 3 4 2 3 0 1/2 1/2 0 1/3 0 1/3 1/3 2 1/4 1/4 0 1/2 0 (b) Suppose we start with 27 robots at each junction. Find the steady state distribution of robots. (Assume that it takes each robot the same amount of time to travel between two adjacent junctions.) 1/3 2/3 0arrow_forward
- Construct the Markov diagram for this game and show that the associate transition matrix T can be written as the following. Show that λ = 1 is an eigenvalue of T. If can answer both (a)and(b), else answer (b).arrow_forwardSuppose a math professor collects data on the probability that students attending a given class meeting will attend the next one. He finds that 95% of students who attended a given class meeting will attend the following class meeting and that 25% of students who do not attend attend a given class meeting will not attend the next one. Build a discrete dynamical system model using linear algebra. Be sure to state your transition matrix explicitly. What percentage of students does your model predict will be attending class meetings by the end of the semester (in the long run)?arrow_forwardPlease help me with this question attached below. Thank you.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Finite Math: Markov Chain Example - The Gambler's Ruin; Author: Brandon Foltz;https://www.youtube.com/watch?v=afIhgiHVnj0;License: Standard YouTube License, CC-BY
Introduction: MARKOV PROCESS And MARKOV CHAINS // Short Lecture // Linear Algebra; Author: AfterMath;https://www.youtube.com/watch?v=qK-PUTuUSpw;License: Standard Youtube License
Stochastic process and Markov Chain Model | Transition Probability Matrix (TPM); Author: Dr. Harish Garg;https://www.youtube.com/watch?v=sb4jo4P4ZLI;License: Standard YouTube License, CC-BY