Thomas' Calculus and Linear Algebra and Its Applications Package for the Georgia Institute of Technology, 1/e
5th Edition
ISBN: 9781323132098
Author: Thomas, Lay
Publisher: PEARSON C
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 10.2, Problem 20E
Consider the mouse in the following maze, which includes “one-way” doors.
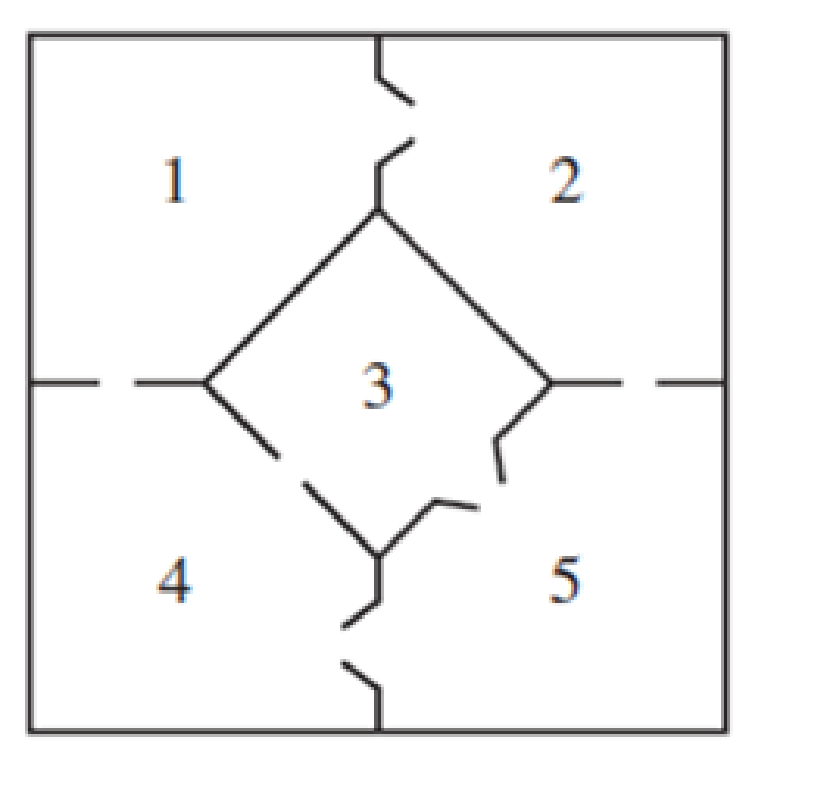
What fraction of the time does the mouse spend in each of the rooms in the maze?
In Exercises 19 and 20, suppose a mouse wanders through the given maze, some of whose doors are “one-way”: they are just large enough for the mouse to squeeze through in only one direction. The mouse still must move into a different room at each time step if possible. When faced with accessible openings into two or more rooms, the mouse chooses them with equal probability.
20. The mouse is placed in room 1 of the maze shown below.
- a. Construct a transition matrix and an initial probability
vector for the mouse’s travels. - b. What are the probabilities that the mouse will be in each of the rooms after 3 moves?
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Monroe County is trying to determine where to place the county fire station. The locations of the county’s four major towns are as follows: (10, 20), (60, 20), (40, 30), and (80, 60) (see Figure 7.50). Town 1 averages 40 fires per year; town 2, 25 fires; town3, 20 fires; and town 4, 30 fires. The county wants to build the fire station in a location that minimizes the average distance that a fire engine must travel to respond to a fire. Because most roads run in either an east-west or a north-south direction, the fire engine must do the same. For example, if the fire station islocated at (30, 40) and a fire occurs at town 4, the fire engine has to travel *80 2 30* 1 * 60 2 40* 5 70 miles to the fire.
a. Determine where the fire station should be located.b. Use SolverTable to see how the optimal location of the fire station changes as the number of fires at town 3 changes.
Suppose Gabe, an elementary school student, has just finished dinner with his mother, Judy. Eyeing the nearby cookie jar, Gabe asks his mother if he can have a cookie for dessert. She tells Gabe that she needs to check his backpack to make sure that he finished his homework. Gabe cannot remember where he left his backpack, but he knows for sure that he did not complete his homework and will not be allowed to eat a cookie. Gabe believes his only option is to quickly steal a cookie while his mother is out of the room.
Judy then leaves the room to look for Gabe's backpack. Assume that Judy could return at any time in the next 9090 seconds with equal p
Judy then leaves the room to look for Gabe's backpack. Assume that Judy could return at any time in the next 9090 seconds with equal probability. For the first 4040 seconds, Gabe sheepishly wonders if he will get caught trying to grab a nearby cookie. After waiting and not seeing his mother, Gabe decides that he needs a cookie and begins to…
Suppose Gabe, an elementary school student, has just finished dinner with his mother, Judy. Eyeing the nearby cookie jar, Gabe asks his mother if he can have a cookie for dessert. She tells Gabe that she needs to check his backpack to make sure that he finished his homework. Gabe cannot remember where he left his backpack, but he knows for sure that he did not complete his homework and will not be allowed to eat a cookie. Gabe believes his only option is to quickly steal a cookie while his mother is out of the room.
Judy then leaves the room to look for Gabe's backpack. Assume that Judy could return at any time in the next 60 seconds with equal probability. For the first 20 seconds, Gabe sheepishly wonders if he will get caught trying to grab a nearby cookie. After waiting and not seeing his mother, Gabe decides that he needs a cookie and begins to take one from the jar.
Assuming it takes Gabe 30 seconds to grab a cookie from the jar and devour it without a trace, what is the…
Chapter 10 Solutions
Thomas' Calculus and Linear Algebra and Its Applications Package for the Georgia Institute of Technology, 1/e
Ch. 10.1 - Fill in the missing entries in the stochastic...Ch. 10.1 - Prob. 2PPCh. 10.1 - In Exercises 1 and 2, determine whether P is a...Ch. 10.1 - In Exercises 1 and 2, determine whether P is a...Ch. 10.1 - Prob. 3ECh. 10.1 - Prob. 4ECh. 10.1 - In Exercises 5 and 6, the transition matrix P for...Ch. 10.1 - Prob. 6ECh. 10.1 - In Exercises 7 and 8, the transition matrix P for...Ch. 10.1 - In Exercises 7 and 8, the transition matrix P for...
Ch. 10.1 - Consider a pair of Ehrenfest urns labeled A and B....Ch. 10.1 - Consider a pair of Ehrenfest urns labeled A and B....Ch. 10.1 - Consider an unbiased random walk on the set...Ch. 10.1 - Consider a biased random walk on the set {1,2,3,4}...Ch. 10.1 - In Exercises 13 and 14, find the transition matrix...Ch. 10.1 - In Exercises 13 and 14, find the transition matrix...Ch. 10.1 - In Exercises 15 and 16, find the transition matrix...Ch. 10.1 - In Exercises 15 and 16, find the transition matrix...Ch. 10.1 - The mouse is placed in room 2 of the maze shown...Ch. 10.1 - The mouse is placed in room 3 of the maze shown...Ch. 10.1 - Prob. 19ECh. 10.1 - In Exercises 19 and 20, suppose a mouse wanders...Ch. 10.1 - Prob. 21ECh. 10.1 - In Exercises 21 and 22, mark each statement True...Ch. 10.1 - The weather in Charlotte, North Carolina, can be...Ch. 10.1 - Suppose that whether it rains in Charlotte...Ch. 10.1 - Prob. 25ECh. 10.1 - Consider a set of five webpages hyperlinked by the...Ch. 10.1 - Consider a model for signal transmission in which...Ch. 10.1 - Consider a model for signal transmission in which...Ch. 10.1 - Prob. 29ECh. 10.1 - Another model for diffusion is called the...Ch. 10.1 - To win a game in tennis, one player must score...Ch. 10.1 - Volleyball uses two different scoring systems in...Ch. 10.1 - Prob. 33ECh. 10.2 - Consider the Markov chain on {1, 2, 3} with...Ch. 10.2 - In Exercises 1 and 2, consider a Markov chain on...Ch. 10.2 - Prob. 2ECh. 10.2 - In Exercises 3 and 4, consider a Markov chain on...Ch. 10.2 - Prob. 4ECh. 10.2 - Prob. 5ECh. 10.2 - In Exercises 5 and 6, find the matrix to which Pn...Ch. 10.2 - In Exercises 7 and 8, determine whether the given...Ch. 10.2 - Prob. 8ECh. 10.2 - Consider a pair of Ehrenfest urns with a total of...Ch. 10.2 - Consider a pair of Ehrenfest urns with a total of...Ch. 10.2 - Consider an unbiased random walk with reflecting...Ch. 10.2 - Consider a biased random walk with reflecting...Ch. 10.2 - Prob. 13ECh. 10.2 - In Exercises 13 and 14, consider a simple random...Ch. 10.2 - In Exercises 15 and 16, consider a simple random...Ch. 10.2 - In Exercises 15 and 16, consider a simple random...Ch. 10.2 - Prob. 17ECh. 10.2 - Prob. 18ECh. 10.2 - Prob. 19ECh. 10.2 - Consider the mouse in the following maze, which...Ch. 10.2 - In Exercises 21 and 22, mark each statement True...Ch. 10.2 - In Exercises 21 and 22, mark each statement True...Ch. 10.2 - Prob. 23ECh. 10.2 - Suppose that the weather in Charlotte is modeled...Ch. 10.2 - In Exercises 25 and 26, consider a set of webpages...Ch. 10.2 - In Exercises 25 and 26, consider a set of webpages...Ch. 10.2 - Prob. 27ECh. 10.2 - Consider beginning with an individual of known...Ch. 10.2 - Prob. 29ECh. 10.2 - Consider the Bernoulli-Laplace diffusion model...Ch. 10.2 - Prob. 31ECh. 10.2 - Prob. 32ECh. 10.2 - Prob. 33ECh. 10.2 - Let 0 p, q 1, and define P = [p1q1pq] a. Show...Ch. 10.2 - Let 0 p, q 1, and define P = [pq1pqq1pqp1pqpq]...Ch. 10.2 - Let A be an m m stochastic matrix, let x be in m...Ch. 10.2 - Prob. 37ECh. 10.2 - Consider a simple random walk on a finite...Ch. 10.2 - Prob. 39ECh. 10.3 - Consider the Markov chain on {1, 2, 3, 4} with...Ch. 10.3 - Prob. 1ECh. 10.3 - In Exercises 16, consider a Markov chain with...Ch. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Consider the mouse in the following maze from...Ch. 10.3 - Prob. 8ECh. 10.3 - Prob. 9ECh. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Consider an unbiased random walk with absorbing...Ch. 10.3 - In Exercises 13 and 14, consider a simple random...Ch. 10.3 - Prob. 14ECh. 10.3 - In Exercises 15 and 16, consider a simple random...Ch. 10.3 - In Exercises 15 and 16, consider a simple random...Ch. 10.3 - Consider the mouse in the following maze from...Ch. 10.3 - Consider the mouse in the following maze from...Ch. 10.3 - Prob. 19ECh. 10.3 - In Exercises 19 and 20, consider the mouse in the...Ch. 10.3 - Prob. 21ECh. 10.3 - Prob. 22ECh. 10.3 - Suppose that the weather in Charlotte is modeled...Ch. 10.3 - Prob. 24ECh. 10.3 - The following set of webpages hyperlinked by the...Ch. 10.3 - The following set of webpages hyperlinked by the...Ch. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Prob. 29ECh. 10.3 - Prob. 30ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 32ECh. 10.3 - Prob. 33ECh. 10.3 - In Exercises 33 and 34, consider the Markov chain...Ch. 10.3 - Prob. 35ECh. 10.3 - Prob. 36ECh. 10.4 - Consider the Markov chain on {1, 2, 3, 4} with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 7-10, consider a simple random walk...Ch. 10.4 - In Exercises 7-10, consider a simple random walk...Ch. 10.4 - In Exercises 7-10, consider a simple random walk...Ch. 10.4 - In Exercises 7-10: consider a simple random walk...Ch. 10.4 - Reorder the states in the Markov chain in Exercise...Ch. 10.4 - Reorder the states in the Markov chain in Exercise...Ch. 10.4 - Reorder the states in the Markov chain in Exercise...Ch. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Find the transition matrix for the Markov chain in...Ch. 10.4 - Find the transition matrix for the Markov chain in...Ch. 10.4 - Consider the mouse in the following maze from...Ch. 10.4 - Consider the mouse in the following maze from...Ch. 10.4 - In Exercises 21-22, mark each statement True or...Ch. 10.4 - In Exercises 21-22, mark each statement True or...Ch. 10.4 - Confirm Theorem 5 for the Markov chain in Exercise...Ch. 10.4 - Prob. 24ECh. 10.4 - Consider the Markov chain on {1, 2, 3} with...Ch. 10.4 - Follow the plan of Exercise 25 to confirm Theorem...Ch. 10.4 - Prob. 27ECh. 10.4 - Prob. 28ECh. 10.4 - Prob. 29ECh. 10.5 - Prob. 1PPCh. 10.5 - Consider a Markov chain on {1, 2, 3, 4} with...Ch. 10.5 - Prob. 1ECh. 10.5 - Prob. 2ECh. 10.5 - In Exercises 13, find the fundamental matrix of...Ch. 10.5 - Prob. 4ECh. 10.5 - Prob. 5ECh. 10.5 - Prob. 6ECh. 10.5 - Prob. 7ECh. 10.5 - Prob. 8ECh. 10.5 - Prob. 9ECh. 10.5 - Prob. 10ECh. 10.5 - Prob. 11ECh. 10.5 - Prob. 12ECh. 10.5 - Consider a simple random walk on the following...Ch. 10.5 - Consider a simple random walk on the following...Ch. 10.5 - Prob. 15ECh. 10.5 - Prob. 16ECh. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - Consider the mouse in the following maze from...Ch. 10.5 - In Exercises 21 and 22, mark each statement True...Ch. 10.5 - Prob. 22ECh. 10.5 - Suppose that the weather in Charlotte is modeled...Ch. 10.5 - Suppose that the weather in Charlotte is modeled...Ch. 10.5 - Consider a set of webpages hyperlinked by the...Ch. 10.5 - Consider a set of webpages hyperlinked by the...Ch. 10.5 - Exercises 27-30 concern the Markov chain model for...Ch. 10.5 - Exercises 27-30 concern the Markov chain model for...Ch. 10.5 - Exercises 27-30 concern the Markov chain model for...Ch. 10.5 - Exercises 27-30 concern the Markov chain model for...Ch. 10.5 - Exercises 31-36 concern the two Markov chain...Ch. 10.5 - Exercises 31-36 concern the two Markov chain...Ch. 10.5 - Exercises 31-36 concern the two Markov chain...Ch. 10.5 - Prob. 34ECh. 10.5 - Prob. 35ECh. 10.5 - Prob. 36ECh. 10.5 - Consider a Markov chain on {1, 2, 3, 4, 5, 6} with...Ch. 10.5 - Consider a Markov chain on {1,2,3,4,5,6} with...Ch. 10.5 - Prob. 39ECh. 10.6 - Let A be the matrix just before Example 1. Explain...Ch. 10.6 - Prob. 2PPCh. 10.6 - Prob. 1ECh. 10.6 - Prob. 2ECh. 10.6 - Prob. 3ECh. 10.6 - Prob. 4ECh. 10.6 - Prob. 5ECh. 10.6 - Prob. 6ECh. 10.6 - Major League batting statistics for the 2006...Ch. 10.6 - Prob. 8ECh. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - Prob. 11ECh. 10.6 - Prob. 12ECh. 10.6 - Prob. 14ECh. 10.6 - Prob. 15ECh. 10.6 - Prob. 16ECh. 10.6 - Prob. 17ECh. 10.6 - In the previous exercise, let p be the probability...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- suppose Gabe , an elementary school student , has just finished dinner with his mother , judy. Eyeing the nearby cookie jar, Gabe asks his mother if he can have cookie foe dessert. She tells Gabe that she needs to check his backpack to make sure that he finished his homework. Gabe cannot remember where he left his backpack, but he knows for sure that he did not complete his homework and will not be allowed to eat a cookie. Gabe believes his only option is to quickly steal a cookie while his mother is out of the room. Judy then leaves the room to look for Gabes backpack. Assume that judy could return at any time in the next 60 seconds with equal probability . For the first 20 seconds, Gabe sheepishly wonders if he will get caught trying to grab a nearby cookie. After waiting and not seeing his mother , Gabe decides that he needs a cookie and begins to take one from the jar. Assuming it takes Gabe 30 seconds to grab a cookie from the jar and devour it without a trace, what is the…arrow_forwardMeghan is a psychology major who is testing a maze for a group of mice to navigate. In order for it to be productive for a class project, she would like the average time for a mouse to complete the maze to be 90 seconds. She randomly selects 28 mice and has each mouse complete the maze. Meghan records the time, in seconds, that each mouse needed to complete the maze. The results are provided in the accompanying data table. Based on research and previous results, Meghan assumes that the population is normally distributed and the population standard deviation is 5.80 seconds. Use Excel to test whether the mean amount of time a mouse completes the maze is 90 seconds, and then draw a conclusion in the context of the problem, where α=0.10. Time (seconds) 85.71 93.16 87.00 89.71 94.26 92.05 86.16 82.16 94.76 HelpCopy to ClipboardDownload CSV Select the correct answer below:…arrow_forwardIs a basketball player's ability to make free throws different when they get their own rebound or when someone else gets their rebound for them? This is what student researchers wanted to explore. The researchers used students (20 females and 20 males) taking a college physical education class as their subjects. The students each attempted 10 shots from the free throw line where they had to get their own rebound and 10 shots where someone else got their rebound and passed the ball back to them while they stayed on the free throw line. They randomly determined the order that they took these shots, with some getting their own rebounds first and some having someone else get the rebounds first. Here are the hypotheses in the picture:arrow_forward
- An archery target consists of a gold circle with radius of 5 inches surrounded by a red ring whose diameter is 20 inches. Next, there are three progressively larger rings – blue, black, and white. The diameter of each ring is 10 inches larger than the diameter of the previous ring. John is a beginner so his aim is poor and, if his arrow hits the target, its location on the target is completely at random. John shoots and then yells, “I hit it!” Without using your calculator, find the following probabilities. Write the answers as a percentage. a) The probability his arrow landed in the gold circle is ______. b) The probability his arrow landed in the white area is ______. c) The probability his arrow landed in the red or the blue area is ______.arrow_forward5. Stephanie's school is selling tickets to the annual dance competition. On the first day of ticket sales the school sold 2 senior citizen tickets and 11 child tickets for a total of $165.20. The school took in $232 the second day selling 8 senior citizen tickets and 12 child tickets. Find the price of a senior citizen ticket and the price of a child ticket. a) Define variables for time and for distance from the trailhead. b) Write a system of two equations to model this situation. c) Solve the system by graphing on Desmos. What is the point of intersection? d) Write an answer to the question using a sentence. 6. Is it possible to draw two lines that intersect in 2 points? Draw an example.arrow_forwardThis question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to the skipped part. Tutorial Exercise A die is a cube with dots on each face. The faces have 1, 2, 3, 4, 5, or 6 dots. The table below is a computer simulation (from the software package Minitab) of the results of rolling a fair die 20 times. DATA DISPLAY ROW C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 1 3 2 4 5 4 5 3 5 3 4 2 5 2 2 2 5 3 2 3 1 4 (a) Assume that each number in the table corresponds to the number of dots on the upward face of the die. Is it appropriate that the same number appears more than once? Why?What is the outcome of the sixth roll?(b) If we simulate more rolls of the die, do you expect to get the same sequence of outcomes? Why or why not? Step 1 (a) Assume that each number in the table corresponds to the number of dots on the upward face of the die. Is it…arrow_forward
- It is claimed that a vitamin supplement helps mice learn to run a maze more quickly and, in fact, to beat a non-treated mouse 70% of the time (whereas without the supplement, it would only win half of the time). To test this claim, you divide a group of 20 mice randomly into ten pairs, giving one of each pair the vitamin supplement. You run each pair through the maze and find that seven out of ten of the mice treated with the vitamin supplement beat the untreated mice. a) What is the probability of obtaining this result if the claim is true? b) What is the probability of obtaining this result if the claim is false (i.e., the supplement has no effect)? c) Suppose before you ran this experiment, you thought it was equally likely that the claim was true or false. After running the experiment, what is your belief? What is the updated probability?arrow_forwardIn a famous study done in the 1960s two dolphins, Doris and Buzz, were trained to work together to earn fish. Doris was shown a light underwater. If the light was on steadily, her partner Buzz on the other side of the tank needed to press a button on the right for them to earn fish. If the light was blinking, he needed to press a button on the left. At one point in the study, the researcher hung a canvas in the middle of the tank in such a way that Buzz could not see the light. After looking at the light, Doris "swam near the curtain and began to whistle loudly. Shortly after that Buzz whistled back and then pressed the correct button". (Tintle, Rossman and Chance, MAA Prep Workshop) Of course, getting it right once was not enough to convince the scientists that there was really communication going on. It turned out, that in 15 out of 16 trials the dolphin pushed the correct button. Of course, it is possible that this happened just out of random chance - that the second dolphin just…arrow_forwardIn a famous study done in the 1960s two dolphins, Doris and Buzz, were trained to work together to earn fish. Doris was shown a light underwater. If the light was on steadily, her partner Buzz on the other side of the tank needed to press a button on the right for them to earn fish. If the light was blinking, he needed to press a button on the left. At one point in the study, the researcher hung a canvas in the middle of the tank in such a way that Buzz could not see the light. After looking at the light, Doris “swam near the curtain and began to whistle loudly. Shortly after that Buzz whistled back and then pressed the [correct] button”. (Tintle, Rossman and Chance, MAA Prep Workshop) Of course, getting it right once was not enough to convince the scientists that there was really communication going on. It turned out, that in 15 out of 16 trials the dolphin pushed the correct button. Of course, it is possible that this happened just out of random chance - that the second dolphin just…arrow_forward
- Many animals, including humans, tend to avoid directeye contact and even patterns that look like eyes.Some insects, including moths, have evolved eye-spotpatterns on their wings to help ward off predators.Scaife (1976) reports a study examining how eye-spotpatterns affect the behavior of birds. In the study, thebirds were tested in a box with two chambers andwere free to move from one chamber to another. Inone chamber, two large eye-spots were painted onone wall. The other chamber had plain walls. Theresearcher recorded the amount of time each birdspent in the plain chamber during a 60-minute session.Suppose the study produced a mean of M = 34.5 minutes on the plain chamber with SS = 210 for a sample of n = 15 birds. (Note: If the eye spots have no effect,then the birds should spend an average of μ = 30minutes in each chamber.)a. Is this sample sufficient to conclude that the eyespots have a significant influence on the birds’behavior? Use a two-tailed test with α = .05.b. Compute the…arrow_forwardIn a classic study of problem solving, Duncker (1945) asked participants to mount a candle on a wall in an upright position so that it would burn normally. One group was given a candle, a book of matches, and a box of tacks. A second group was given the same items, except that the tacks and the box were presented separately as two distinct items. The solution to this problem involves using the tacks to mount the box on the wall, creating a shelf for the candle. Duncker reasoned that the first group of participants would have trouble seeing a new function for the box (a shelf) because it was already serving a function (holding tacks). For each participant, the amount of time to solve the problem was recorded. Data similar to Duncker’s are as follows. Time to Solve Problem (in sec.) Box of Tacks Tacks and Box Separate 128 42 160…arrow_forwardthe following table shows the amount spent by four U.S. airlines to fly one available seat 1 mile in the second quarter of 2020.† Set up a system and then solve using technology. Airline United American JetBlue Southwest Cost per 1,000 miles ($) 181 197 123 134 Suppose that, on a 3,000-mile New York to Los Angeles flight, United, American, and Southwest flew a total of 205 empty seats, costing them a total of $103,830. If United had three times as many empty seats as American, how many empty seats did each of these three airlines carry on its flight? United _____empty seats American _____empty seats Southwest ____empty seatsarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
Finite Math: Markov Chain Example - The Gambler's Ruin; Author: Brandon Foltz;https://www.youtube.com/watch?v=afIhgiHVnj0;License: Standard YouTube License, CC-BY
Introduction: MARKOV PROCESS And MARKOV CHAINS // Short Lecture // Linear Algebra; Author: AfterMath;https://www.youtube.com/watch?v=qK-PUTuUSpw;License: Standard Youtube License
Stochastic process and Markov Chain Model | Transition Probability Matrix (TPM); Author: Dr. Harish Garg;https://www.youtube.com/watch?v=sb4jo4P4ZLI;License: Standard YouTube License, CC-BY