Thomas' Calculus and Linear Algebra and Its Applications Package for the Georgia Institute of Technology, 1/e
5th Edition
ISBN: 9781323132098
Author: Thomas, Lay
Publisher: PEARSON C
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 10.4, Problem 10E
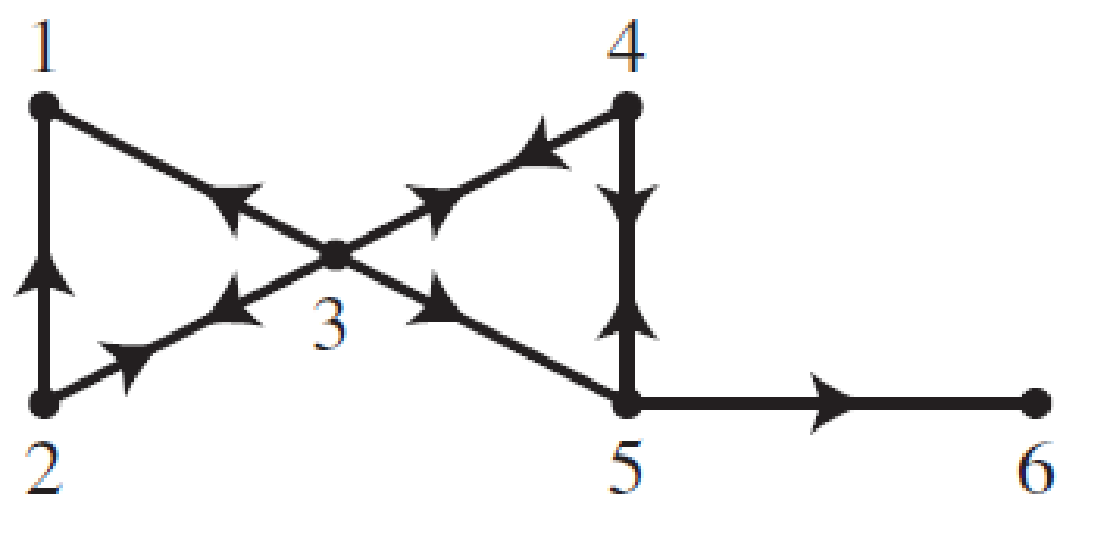
In Exercises 7-10: consider a simple random walk on the given directed graph. Identify the-communication classes of this Markov chain as -recurrent or transient, and find the period of each communication class.
10. 
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Each item is inspected and is declared to either pass or fail. The machine can work in automatic or manual mode. If it outputs two failed items in a row in automatic mode, it is switched to manual. Once it produces two passing items in a row in manual mode, it is switched back to automatic. Sup- pose that failure rate is a in automatic and b in manual. You modeled the system as a Markov chain with a diagram given below, where states represent the mode and the status of the previously man- ufactured item, so for example, state “manual-1 success” represents that the machine is in manual mode and the previous item passed.
A system consists of five components, each can be operational or not. Each day one operational component is used and it will fail with probability 20%. Any time there no operational components at the end of a day, maintenance will be performed and all non-operational components will be repaired (with probability 1). The system does not perform any other tasks on the day of repairs.
Model the system as a Markov chain
Write down equations for determining long-run proportions.
Suppose that you are interested in the average number of days that the system is under repair. Explain how you would find it using your model.
Please describe the steps you used to get the solution to the problem provided in the image below.
Chapter 10 Solutions
Thomas' Calculus and Linear Algebra and Its Applications Package for the Georgia Institute of Technology, 1/e
Ch. 10.1 - Fill in the missing entries in the stochastic...Ch. 10.1 - Prob. 2PPCh. 10.1 - In Exercises 1 and 2, determine whether P is a...Ch. 10.1 - In Exercises 1 and 2, determine whether P is a...Ch. 10.1 - Prob. 3ECh. 10.1 - Prob. 4ECh. 10.1 - In Exercises 5 and 6, the transition matrix P for...Ch. 10.1 - Prob. 6ECh. 10.1 - In Exercises 7 and 8, the transition matrix P for...Ch. 10.1 - In Exercises 7 and 8, the transition matrix P for...
Ch. 10.1 - Consider a pair of Ehrenfest urns labeled A and B....Ch. 10.1 - Consider a pair of Ehrenfest urns labeled A and B....Ch. 10.1 - Consider an unbiased random walk on the set...Ch. 10.1 - Consider a biased random walk on the set {1,2,3,4}...Ch. 10.1 - In Exercises 13 and 14, find the transition matrix...Ch. 10.1 - In Exercises 13 and 14, find the transition matrix...Ch. 10.1 - In Exercises 15 and 16, find the transition matrix...Ch. 10.1 - In Exercises 15 and 16, find the transition matrix...Ch. 10.1 - The mouse is placed in room 2 of the maze shown...Ch. 10.1 - The mouse is placed in room 3 of the maze shown...Ch. 10.1 - Prob. 19ECh. 10.1 - In Exercises 19 and 20, suppose a mouse wanders...Ch. 10.1 - Prob. 21ECh. 10.1 - In Exercises 21 and 22, mark each statement True...Ch. 10.1 - The weather in Charlotte, North Carolina, can be...Ch. 10.1 - Suppose that whether it rains in Charlotte...Ch. 10.1 - Prob. 25ECh. 10.1 - Consider a set of five webpages hyperlinked by the...Ch. 10.1 - Consider a model for signal transmission in which...Ch. 10.1 - Consider a model for signal transmission in which...Ch. 10.1 - Prob. 29ECh. 10.1 - Another model for diffusion is called the...Ch. 10.1 - To win a game in tennis, one player must score...Ch. 10.1 - Volleyball uses two different scoring systems in...Ch. 10.1 - Prob. 33ECh. 10.2 - Consider the Markov chain on {1, 2, 3} with...Ch. 10.2 - In Exercises 1 and 2, consider a Markov chain on...Ch. 10.2 - Prob. 2ECh. 10.2 - In Exercises 3 and 4, consider a Markov chain on...Ch. 10.2 - Prob. 4ECh. 10.2 - Prob. 5ECh. 10.2 - In Exercises 5 and 6, find the matrix to which Pn...Ch. 10.2 - In Exercises 7 and 8, determine whether the given...Ch. 10.2 - Prob. 8ECh. 10.2 - Consider a pair of Ehrenfest urns with a total of...Ch. 10.2 - Consider a pair of Ehrenfest urns with a total of...Ch. 10.2 - Consider an unbiased random walk with reflecting...Ch. 10.2 - Consider a biased random walk with reflecting...Ch. 10.2 - Prob. 13ECh. 10.2 - In Exercises 13 and 14, consider a simple random...Ch. 10.2 - In Exercises 15 and 16, consider a simple random...Ch. 10.2 - In Exercises 15 and 16, consider a simple random...Ch. 10.2 - Prob. 17ECh. 10.2 - Prob. 18ECh. 10.2 - Prob. 19ECh. 10.2 - Consider the mouse in the following maze, which...Ch. 10.2 - In Exercises 21 and 22, mark each statement True...Ch. 10.2 - In Exercises 21 and 22, mark each statement True...Ch. 10.2 - Prob. 23ECh. 10.2 - Suppose that the weather in Charlotte is modeled...Ch. 10.2 - In Exercises 25 and 26, consider a set of webpages...Ch. 10.2 - In Exercises 25 and 26, consider a set of webpages...Ch. 10.2 - Prob. 27ECh. 10.2 - Consider beginning with an individual of known...Ch. 10.2 - Prob. 29ECh. 10.2 - Consider the Bernoulli-Laplace diffusion model...Ch. 10.2 - Prob. 31ECh. 10.2 - Prob. 32ECh. 10.2 - Prob. 33ECh. 10.2 - Let 0 p, q 1, and define P = [p1q1pq] a. Show...Ch. 10.2 - Let 0 p, q 1, and define P = [pq1pqq1pqp1pqpq]...Ch. 10.2 - Let A be an m m stochastic matrix, let x be in m...Ch. 10.2 - Prob. 37ECh. 10.2 - Consider a simple random walk on a finite...Ch. 10.2 - Prob. 39ECh. 10.3 - Consider the Markov chain on {1, 2, 3, 4} with...Ch. 10.3 - Prob. 1ECh. 10.3 - In Exercises 16, consider a Markov chain with...Ch. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Consider the mouse in the following maze from...Ch. 10.3 - Prob. 8ECh. 10.3 - Prob. 9ECh. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Consider an unbiased random walk with absorbing...Ch. 10.3 - In Exercises 13 and 14, consider a simple random...Ch. 10.3 - Prob. 14ECh. 10.3 - In Exercises 15 and 16, consider a simple random...Ch. 10.3 - In Exercises 15 and 16, consider a simple random...Ch. 10.3 - Consider the mouse in the following maze from...Ch. 10.3 - Consider the mouse in the following maze from...Ch. 10.3 - Prob. 19ECh. 10.3 - In Exercises 19 and 20, consider the mouse in the...Ch. 10.3 - Prob. 21ECh. 10.3 - Prob. 22ECh. 10.3 - Suppose that the weather in Charlotte is modeled...Ch. 10.3 - Prob. 24ECh. 10.3 - The following set of webpages hyperlinked by the...Ch. 10.3 - The following set of webpages hyperlinked by the...Ch. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Prob. 29ECh. 10.3 - Prob. 30ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 32ECh. 10.3 - Prob. 33ECh. 10.3 - In Exercises 33 and 34, consider the Markov chain...Ch. 10.3 - Prob. 35ECh. 10.3 - Prob. 36ECh. 10.4 - Consider the Markov chain on {1, 2, 3, 4} with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 7-10, consider a simple random walk...Ch. 10.4 - In Exercises 7-10, consider a simple random walk...Ch. 10.4 - In Exercises 7-10, consider a simple random walk...Ch. 10.4 - In Exercises 7-10: consider a simple random walk...Ch. 10.4 - Reorder the states in the Markov chain in Exercise...Ch. 10.4 - Reorder the states in the Markov chain in Exercise...Ch. 10.4 - Reorder the states in the Markov chain in Exercise...Ch. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Find the transition matrix for the Markov chain in...Ch. 10.4 - Find the transition matrix for the Markov chain in...Ch. 10.4 - Consider the mouse in the following maze from...Ch. 10.4 - Consider the mouse in the following maze from...Ch. 10.4 - In Exercises 21-22, mark each statement True or...Ch. 10.4 - In Exercises 21-22, mark each statement True or...Ch. 10.4 - Confirm Theorem 5 for the Markov chain in Exercise...Ch. 10.4 - Prob. 24ECh. 10.4 - Consider the Markov chain on {1, 2, 3} with...Ch. 10.4 - Follow the plan of Exercise 25 to confirm Theorem...Ch. 10.4 - Prob. 27ECh. 10.4 - Prob. 28ECh. 10.4 - Prob. 29ECh. 10.5 - Prob. 1PPCh. 10.5 - Consider a Markov chain on {1, 2, 3, 4} with...Ch. 10.5 - Prob. 1ECh. 10.5 - Prob. 2ECh. 10.5 - In Exercises 13, find the fundamental matrix of...Ch. 10.5 - Prob. 4ECh. 10.5 - Prob. 5ECh. 10.5 - Prob. 6ECh. 10.5 - Prob. 7ECh. 10.5 - Prob. 8ECh. 10.5 - Prob. 9ECh. 10.5 - Prob. 10ECh. 10.5 - Prob. 11ECh. 10.5 - Prob. 12ECh. 10.5 - Consider a simple random walk on the following...Ch. 10.5 - Consider a simple random walk on the following...Ch. 10.5 - Prob. 15ECh. 10.5 - Prob. 16ECh. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - Consider the mouse in the following maze from...Ch. 10.5 - In Exercises 21 and 22, mark each statement True...Ch. 10.5 - Prob. 22ECh. 10.5 - Suppose that the weather in Charlotte is modeled...Ch. 10.5 - Suppose that the weather in Charlotte is modeled...Ch. 10.5 - Consider a set of webpages hyperlinked by the...Ch. 10.5 - Consider a set of webpages hyperlinked by the...Ch. 10.5 - Exercises 27-30 concern the Markov chain model for...Ch. 10.5 - Exercises 27-30 concern the Markov chain model for...Ch. 10.5 - Exercises 27-30 concern the Markov chain model for...Ch. 10.5 - Exercises 27-30 concern the Markov chain model for...Ch. 10.5 - Exercises 31-36 concern the two Markov chain...Ch. 10.5 - Exercises 31-36 concern the two Markov chain...Ch. 10.5 - Exercises 31-36 concern the two Markov chain...Ch. 10.5 - Prob. 34ECh. 10.5 - Prob. 35ECh. 10.5 - Prob. 36ECh. 10.5 - Consider a Markov chain on {1, 2, 3, 4, 5, 6} with...Ch. 10.5 - Consider a Markov chain on {1,2,3,4,5,6} with...Ch. 10.5 - Prob. 39ECh. 10.6 - Let A be the matrix just before Example 1. Explain...Ch. 10.6 - Prob. 2PPCh. 10.6 - Prob. 1ECh. 10.6 - Prob. 2ECh. 10.6 - Prob. 3ECh. 10.6 - Prob. 4ECh. 10.6 - Prob. 5ECh. 10.6 - Prob. 6ECh. 10.6 - Major League batting statistics for the 2006...Ch. 10.6 - Prob. 8ECh. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - Prob. 11ECh. 10.6 - Prob. 12ECh. 10.6 - Prob. 14ECh. 10.6 - Prob. 15ECh. 10.6 - Prob. 16ECh. 10.6 - Prob. 17ECh. 10.6 - In the previous exercise, let p be the probability...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Explain how you can determine the steady state matrix X of an absorbing Markov chain by inspection.arrow_forward12. Robots have been programmed to traverse the maze shown in Figure 3.28 and at each junction randomly choose which way to go. Figure 3.28 (a) Construct the transition matrix for the Markov chain that models this situation. (b) Suppose we start with 15 robots at each junction. Find the steady state distribution of robots. (Assume that it takes each robot the same amount of time to travel between two adjacent junctions.)arrow_forwardConsider the Markov chain whose matrix of transition probabilities P is given in Example 7b. Show that the steady state matrix X depends on the initial state matrix X0 by finding X for each X0. X0=[0.250.250.250.25] b X0=[0.250.250.400.10] Example 7 Finding Steady State Matrices of Absorbing Markov Chains Find the steady state matrix X of each absorbing Markov chain with matrix of transition probabilities P. b.P=[0.500.200.210.300.100.400.200.11]arrow_forward
- Please answer ASAP PLEASEarrow_forwardA system consists of five components, each can be operational or not. Each day one operational component is used and it will fail with probability 20%. Suppose there are five repairmen available that can each work on one broken down component per day. Each repairman successfully fixes the component with probability 70% regardless of whether he has worked on it previous days. Model the system as a Markov chain Write down equations for determining long-run proportions. Suppose that you are interested in the average number of repairmen who are working per day. Explain how you would find it using your model. You are not asked to solve any equations here, instead describe how you would use the solutions.arrow_forwardPlease find the transition matrix for this Markov processarrow_forward
- Consider a Markov random process whose state transition diagram is shown in figure below. Write the state transition matrix for the Markov process whose corresponding state transition diagram is shown in the above figure. List the pairs of communicating states. List 2 pairs of accessible states and 2 pairs of inaccessible states. List all the transient states List all the recurrent states Identify the classes of the Markov chain and list the closed and non-closed Find P[X2 = 2 | X1 = 3] Find P[X6 = 4, X5 = 3, X4 = 2, X3 =3, X2 = 2, X1 = 1, X0 =1]. where Xt denotes the state of the random process at time instant t. The initial probability distribution is given by X0 = [2/3 0 0 0 0 0 1/3]. KIndly request you to refer to the screenshot for the figurearrow_forwardPlease show steps to find solution for markov chainarrow_forwardCan someone please help me with this question. I am having so much trouble.arrow_forward
- Please find the transition matrix for this Markov processarrow_forwardModems networked to a mainframe computer system have a limited capacity. is the probability that a user dials into the network when a modem connection is available, and 1/4 is the probability that a call is received when all lines are busy. The system can be considered as a binary Markov chain. Draw the state transition diagram of the Markov chain. i) ii) iii) Find the state transition matrix and the probability state vector p (k). Describe the steady-state behaviour of the system, i.e., find the vector (For a binary Markov chain, =B₁² a) + + pk =a+B \B 1 [3²] ) В (1-α-B) k | α a+ßarrow_forwardA factory worker will quit with probability 1/2 during her first month, with probability 1/4 during her second month and with probability 1/8 after that. Whenever someone quits, their replacement will start at the beginning of the next month. Model the status of each position as a Markov chain with 3 states. Identify the states and transition matrix. Write down the system of equations determining the long-run proportions. Suppose there are 900 workers in the factory. Find the average number of the workers who have been there for more than 2 months.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Finite Math: Markov Chain Example - The Gambler's Ruin; Author: Brandon Foltz;https://www.youtube.com/watch?v=afIhgiHVnj0;License: Standard YouTube License, CC-BY
Introduction: MARKOV PROCESS And MARKOV CHAINS // Short Lecture // Linear Algebra; Author: AfterMath;https://www.youtube.com/watch?v=qK-PUTuUSpw;License: Standard Youtube License
Stochastic process and Markov Chain Model | Transition Probability Matrix (TPM); Author: Dr. Harish Garg;https://www.youtube.com/watch?v=sb4jo4P4ZLI;License: Standard YouTube License, CC-BY